OpenCASCADE Conic to BSpline Curves-Circle

OpenCASCADE Conic to BSpline Curves-Circle

eryar@163.com

Abstract. The conic sections and circles play a fundamental role in CAD/CAM applications. Undoubtedly one of the greatest advantages of NURBS is their capability of precisely representing conic sections and circles, as well as free-form curves and surfaces. We assume a knowledge of conics and circles, the purpose of this paper is to study them in the framework of their representation as NURBS curves.

Key Words. OpenCASCADE, Conic Curves, Circle, Convert, BSpline Curve

1. Introduction

B样条技术在自由曲线曲面的设计和表示方面显示出了其卓越的优点，但在表示初等曲线曲面时却遇到了麻烦。在很多应用领域，例如飞机、造船、汽车等工业中，圆弧、椭圆弧、抛物线、圆柱面、球面、圆锥面、圆环面等经常出现，这些形状都表示精确且往往要求较高的加工精度。传统的B样条技术只能精确地表示抛物线、抛物面，对其他的二次曲线曲面只能近似表示。因此，在一个造型系统内无法用一种统一的形式表示曲线曲面，因而使得系统的开发复杂化。非均匀有理B样条（NURBS）技术正是在这样的需求背景下逐步发展成熟起来的。

NURBS曲线曲面能够迅速接受的主要原因在于：

v NURBS技术可以精确表示规则曲线与曲面（如圆锥曲线、二次曲面、旋转曲面等）。

v 可以把规则曲线曲面和自由曲线曲面统一起来表示。因而便于用统一的算法进行处理和使用统一的数据库进行存储，程序量可明显减少；

v 由于增加了额外的自由度（权因子），若应用得当，有利于曲线曲面形状的控制和修改。

v NURBS技术是非有理Bezier曲线的和B样条形式的真正推广；

本文主要介绍圆的NURBS表示方法，即如何将圆转换为NURBS曲线。

2.The Effect of Multiple Knots (Multiplicity)

重节点的定义为在节点序列中顺序r个节点相同或xi重复出现r次，称为该节点xi具有重复度r（Multiplicity）。在OpenCASCADE中B样条曲线类的构造就是用的节点Knots及其对应的重复度Multiplicities来实现的，如下所示：

  //!  Creates a  non-rational B_spline curve   on  the <br>
//!         basis <Knots, Multiplicities> of degree <Degree>. <br>
  Standard_EXPORT   Geom_BSplineCurve(const TColgp_Array1OfPnt& Poles,const TColStd_Array1OfReal& Knots,const TColStd_Array1OfInteger& Multiplicities,const Standard_Integer Degree,const Standard_Boolean Periodic = Standard_False);

重节点有如下重要性质：

v 重节点连续阶性质。在每个节点区间(uj, uj+1)内部，Bi,p(u)为多项式函数，因此，所有导数存在。在一个节点uj处Bi,p(u)是p-mj次连续可微的，此处mj是该点的重数。所以增加次数，则增加连续性，而增加节点的重数，则降低连续性。通常为保证连续性，节点的最高重数为p；

v 重节点的插值基函数性质。当节点向量中的内节点uj的重数为p，则只有定义在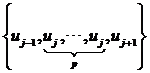上的基函数在uj上取值为1，其余基函数在uj取值为0。当节点向是中的端节点uj的重数为p+1，则只有定义在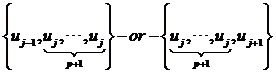上的基函数在uj取值为1，其余基函数在uj取值为0。

如下图所示为具有重节点的B样条基函数：

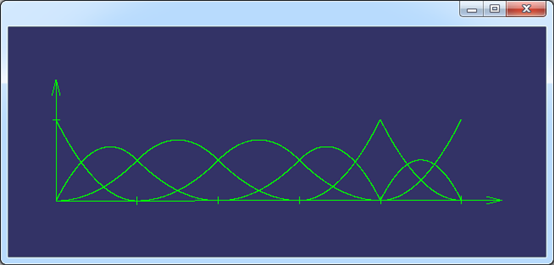
Figure 2.1 U={0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5} p = 2 B-spline Basis Function

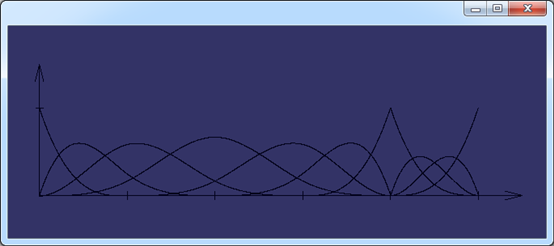
Figure 2.2 U={0, 0, 0, 0,1, 2, 3, 4, 4,4, 5, 5, 5,5} p = 3 B-spline Basis Function

由上图可知，重节点的出现对B样条曲线有影响，如下所述：

当节点向量内部某节点的重数与次数相同时，则B样条基数在此节点处的值为1，即由此得到的B样条曲线的控制顶点将与B样条曲线上的点重合。所以利用重节点的插值性质可以在B样条曲线内部构造尖点与尖角。

当端节点重数为p时，p次的B样条曲线的端点将与相应的控制多边形的端点相重，曲线在端节点处与控制多边形相切。

当端节点重数为p+1时，p次B样条曲线就具有与p次Bezier曲线相同的端点几何性质。这时如果B样条曲线的定义域仅有一个非零节点区间，则所定义的B样条曲线就是Bezier曲线。由此可知，B样条方法是Bezier方法的强有力的推广。

理解重节点的作用非常重要，利用重节点技术可用来控制B样条基以达到控制整条曲线在节点处的连续性的目的。

3.Construction of Circles

如前所述，NURBS技术是Bezier技术的推广。实际上，有理Bezier技术就可精确地表示圆锥曲线。由有理Bezier曲线的公式得二次有理Bezier曲线弧的表示形式为：

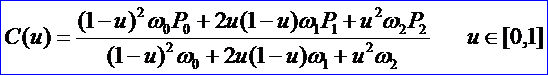
称k为形状不变因子，公式如下所示：

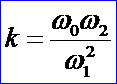
一段小于180度的圆弧也可以用二次有理Bezier曲线来表示。由于对称性，P0P1P2必须是一个等腰三角形，满足P0P1=P1P2，计算得ω1＝cos(θ)。

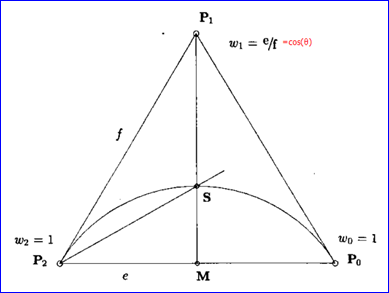
Figure 3.1 圆心角度小于180度圆弧的二次有理Bezier表示

大于180度的圆弧可以使用多段小圆弧拼接而成。得用重节点技术，使多段圆弧拼接起来。重节点的一种方法是使用2重节点，在有i段圆弧时，其内部节点值可取为1/i，…，i-1/i，权因子的取法不变。

以180度的圆弧为例，可以使用两段90度圆弧拼接而成。节点矢量可取为U＝{0，0，0，1/2，1/2，1，1，1}。权因子可以取为ω1＝ω3＝cos45，ω0＝ω2＝ω4＝1。则对应的B样条基函数及B样条曲线如下图所示：

由图可知基函数在1/2处取值为1，则对应的B样条曲线上的值与控制顶点重合。

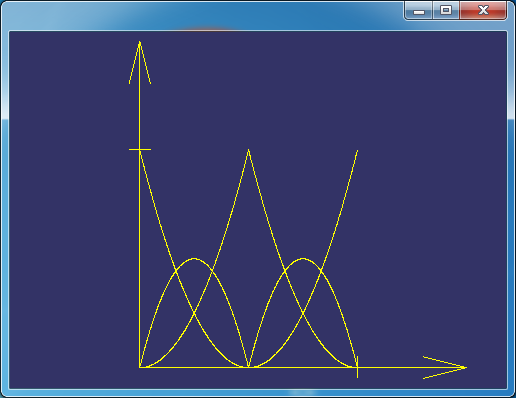
Figure 3.2 U＝{0，0，0，1/2，1/2，1，1，1} B Spline Basis

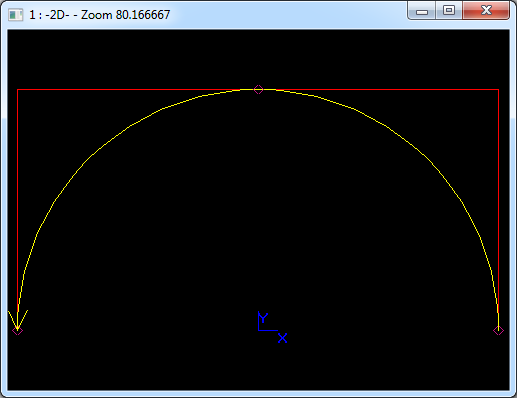
Figure 3.3 Semi-Circle B Spline Curve

用四段圆弧组成一个整圆，节点矢量为U＝{0，0，0，1/4，1/4，2/4，2/4，3/4，3/4，1，1，1}，权因子取{1，sqrt(2)/2，1，1，sqrt(2)/2，1，1，sqrt(2)/2，1}，使用Tcl脚本在Draw Test Harness中显示如下图所示：

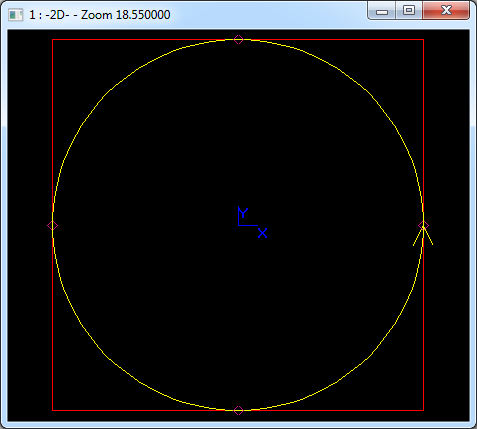
Figure 3.4 A Circle represented by 4 arcs

Tcl代码如下所示：

#
#    Copyright (c) 2014 eryar All Rights Reserved.
#
#        File    : colorscale.tcl
#        Author  : eryar@163.com
#        Date    : 2014-10-13 18:10
#        Version : 1.0v
#
#    Description : Demonstrate the rational 2d Bezier curve
#                  and BSpline curve.
#

pload MODELING

# use 4 arc to composite a circle
2dbsplinecurve c2  \
    /  /  /    \
    \
   sqrt(2.0)/2.0 \
    \
 -  sqrt(2.0)/2.0 \
 -   \
 - - sqrt(2.0)/2.0 \
  -  \
  - sqrt(2.0)/2.0 \

# fit the 2d view
v2d
2dfit

也可用位于三角形上的控制点来表示圆，如下图所示：

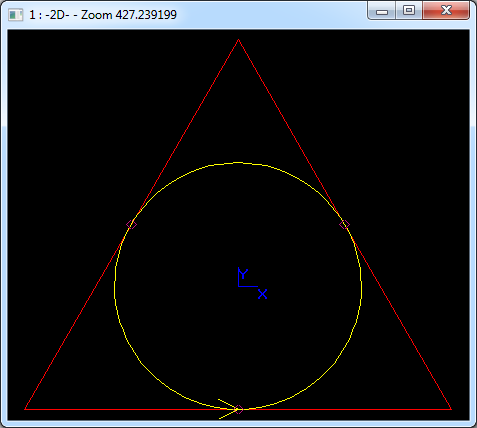
Figure 3.5 A Circle represented by 3 arcs

相应的Tcl代码如下所示：

pload MODELING
# a 2d periodic circle (parameter from 0 to 2*pi !!)
dset h sqrt()/
2dpbsplinecurve c3  \
   pi/1.5  pi/0.75  *pi  \
 -h/  \
0.5 -h/ 0.5 \
0.25 h/  \
 *h/ 0.5 \
-0.25 h/  \
-0.5 -h/ 0.5 \
 -h/
# fit the 2d view
v2d
2dfit

4.Code Analysis

OpenCASCADE中提供了将圆转换为NURBS曲线的功能，转换后得到的NURBS曲线的参数范围不再是[0，1]。下面给出具体的实例：

void TestCircleConvert(void)
{
    gp_Circ2d aCircle;
    aCircle.SetRadius(1.0);
    Convert_ParameterisationType aType = Convert_TgtThetaOver2;
    Convert_CircleToBSplineCurve aConvertor(aCircle, aType);

    Handle_Geom_Circle aGeomCircle = GC_MakeCircle(gp::XOY(), 1.0);
　　Handle_Geom_BSplineCurve aBSplineCurve =
　　  GeomConvert::CurveToBSplineCurve(aGeomCircle, aType);

    std::cout << "Convert Circle to BSpline Curve: " << std::endl;
    DumpConvertorInfo(aConvertor);
}

int main(int argc, char* argv[])
{
    TestCircleConvert();

    return ;
}

结果如下图所示：

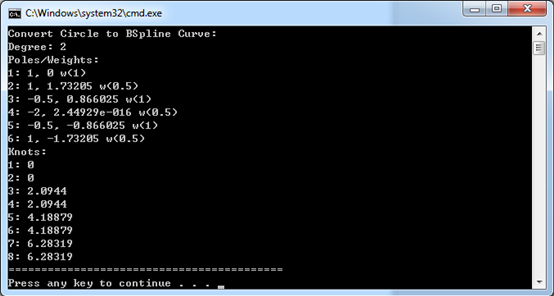
由上述结果可知，在默认参数化的情况下是按三段圆弧来拼接成一个整圆的。也可指定不同的参数化类型，将会得到不同的NURBS曲线。次数也可能不是2次，会用高次的NURBS曲线来表示圆。

5.Conclusion

利用重节点技术及二次有理B样条的性质，可以用NURBS来精确表示圆。选择不同的控制顶点，得到的圆的参数化效果也有所不同。

将常用的圆锥曲线用NURBS曲线来表示，即说明可以用NURBS曲线来统一表示圆锥曲线及自由曲线。这说明在理论上，一个造型内核的曲线可以只用一个类来表示，这个类对应OpenCASCADE中的Geom_BSplineCurve。

使用Tcl可以在Draw Test Harness中方便地产生NURBS曲线，从而可以快速验证一些算法的正确性。

6. References

1． 赵罡，穆国旺，王拉柱译Les Piegl，Wayne Tiller The NURBS Book(Second Edition) 2010 清华大学出版社

2． 莫容，常智勇 计算机辅助几何造型技术 2009 科学出版社

3． 朱心雄等，自由曲线曲面造型技术，2000，科学出版社

4． Kelly Dempski, Focus on Curves and Surface, 2003, Premier Press

5． 王仁宏，李崇君，朱春钢 计算几何教程 2008 科学出版社

PDF version and Tcl script: OpenCASCADE Conic to BSpline Curves-Circle