HDU 5489 Difference of Clustering 图论

Difference of Clustering

Problem Description

Given two clustering algorithms, the old and the new, you want to find the difference between their results. 
A clustering algorithm takes many member entities as input and partition them into clusters. In this problem, a member entity must be clustered into exactly one cluster. However, we don’t have any pre-knowledge of the clusters, so different algorithms may produce different number of clusters as well as different cluster IDs. One thing we are sure about is that the memberIDs are stable, which means that the same member ID across different algorithms indicates the same member entity.
To compare two clustering algorithms, we care about three kinds of relationship between the old clusters and the new clusters: split, merge and 1:1. Please refer to the figure below.

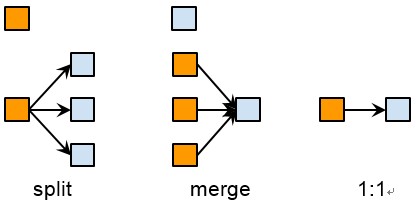
Let’s explain them with examples. Say in the old result, m0, m1, m2 are clustered into one cluster c0, but in the new result, m0 and m1 are clustered into c0, but m2 alone is clustered into c1. We denote the relationship like the following:
●  In the old, c0 = [m0, m1, m2]
●  In the new, c0 = [m0, m1], c1 = [m2]
There is no other members in the new c0 and c1. Then we say the old c0 is split into new c0 and new c1. A few more examples:
●  In the old, c0 = [m0, m1, m2]
●  In the new, c0 = [m0, m1, m2]. 
This is 1:1.
●  In the old, c0 = [m0, m1], c1 = [m2]
●  In the new, c0 = [m0, m1, m2]
This is merge. Please note, besides these relationship, there is another kind called “n:n”:
●  In the old, c0 = [m0, m1], c1 = [m2, m3]
●  In the new, c0 = [m0, m1, m2], c1 = [m3]
We don’t care about n:n. 
In this problem, we will give you two sets of clustering results, each describing the old and the new. We want to know the total number of splits, merges, and 1:1 respectively.

 

Input

The first line of input contains a number T indicating the number of test cases (T≤100).
Each test case starts with a line containing an integer N indicating the number of member entities (0≤N≤106 ). In the following N lines, the i-th line contains two integers c1 and c2, which means that the member entity with ID i is partitioned into cluster c1 and cluster c2 by the old algorithm and the new algorithm respectively. The cluster IDs c1 and c2 can always fit into a 32-bit signed integer.

 

Output

For each test case, output a single line consisting of “Case #X: A B C”. X is the test case number starting from 1. A, B, and C are the numbers of splits, merges, and 1:1s.

 

Sample Input

2
3
0 0
0 0
0 1
4
0 0
0 0
1 1
1 1

 

Sample Output

Case #1: 1 0 0
Case #2: 0 0 2

 

Source

2015 ACM/ICPC Asia Regional Hefei Online

 

题意：  给你n个关系，每个关系是a,b，表示a,b间连了一条边（注意要去重边），问你一对多，多对一，1对1的情况分别有多少种

         例如：样例1就是

                              0->1&&0->0

题解：  图论中的求出度，入度判断是哪种，STL大法

///
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<queue>
#include<cmath>
#include<map>
#include<bitset>
#include<set>
#include<vector>
using namespace std ;
typedef __int64 ll;
#define mem(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,127,sizeof(a));
#define memfy(a)  memset(a,-1,sizeof(a));
#define TS printf("111111\n");
#define FOR(i,a,b) for( int i=a;i<=b;i++)
#define FORJ(i,a,b) for(int i=a;i>=b;i--)
#define READ(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define mod 1000000007
#define inf 100000000
inline ll read()
{
    ll x=,f=;
    char ch=getchar();
    while(ch<''||ch>'')
    {
        if(ch=='-')f=-;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=x*+ch-'';
        ch=getchar();
    }
    return x*f;
}
//****************************************

#define maxn 1000000+6
struct ss
{
    int to,next;
} e[maxn];
struct node
{
    int x,index;//0,1;
};
int head[maxn],n,a,b,t,in[maxn][],A,B,C;
map<pair<int ,int >,int  >mp;
map<int ,int >vis,vis2;
map<int ,vector<int > >mpp,mpp2;
vector<int >V1,V2;
vector<int >::iterator it;;
int main()
{

    int T=read();
    int oo=;
    while(T--)
    {
        // init();
        scanf("%d",&n);
        mp.clear();
        V1.clear();
        V2.clear();
        mpp2.clear();
        mpp.clear();
        vis.clear();
        vis2.clear();
        int k=;
        FOR(i,,n)
        {
            scanf("%d%d",&a,&b);
            if(mp[make_pair(a,b)])continue;
            mpp[a].push_back(b);
            mpp2[b].push_back(a);
            if(!vis[a])
            V1.push_back(a);
            if(!vis2[b])
            V2.push_back(b);
            vis[a]=;
            vis2[b]=;
            mp[make_pair(a,b)]=;
        }
        A=;
        B=;
        C=;
        int sum;
        for(int i=; i<V1.size(); i++)
        {
            sum=;
            for(it=mpp[V1[i]].begin(); it!=mpp[V1[i]].end(); it++)
            {
                sum+=mpp2[*it].size();
            }
            if(sum==mpp[V1[i]].size())
            {
                if(sum==)
                    C++;
                else
                {
                    A++;
                }
            }
        }
        for(int i=; i<V2.size(); i++)
        {
            sum=;
            for(it=mpp2[V2[i]].begin(); it!=mpp2[V2[i]].end(); it++)
            {
                sum+=mpp[*it].size();
            }
            if(sum==mpp2[V2[i]].size())
            {  //cout<<mpp[V2[i]].size()<<endl;
                if(sum==)
                    C++;
                else
                {
                    B++;
                }
            }
        }
        printf("Case #%d: ",oo++);
        cout<<A<<" "<<B<<" "<<C/<<endl;

    }
    return ;
}

代码