LOGISTIC回归分析

前面的博客有介绍过对连续的变量进行线性回归分析，从而达到对因变量的预测或者解释作用。那么如果因变量是离散变量呢？在做行为预测的时候通常只有“做”与“不做的区别”、“0”与“1”的区别，这是我们就要用到logistic分析（逻辑回归分析，非线性模型）。

参数解释（对变量的评价）

发生比(odds)： ODDS=事件发生概率/事件不发生的概率=P/(1-P)

发生比率（odds ratio）：odds ratio=odds_B/odds_A       (组B相对于组A更容易发生的比率）

注：odds ratio大于1或者小于1都有意义，代表自变量的两个分组有差异性，对因变量的发生概率有作用。若等于1的话，该组变量对事件发生概率没有任何作用。

参数估计方法

线性回归中，主要是采用最小二乘法进行参数估计，使其残差平方和最小。同时在线性回归中最大似然估计和最小二乘发估计结果是一致的，但不同的是极大似然法可以用于非线性模型，又因为逻辑回归是非线性模型，所以逻辑回归最常用的估计方法是极大似然法。

极大似然公式：L(Θ)=P(Y₁)P(Y₂)...p(Y_N)            P为事件发生概率P_I=1/(1+E^-(α+βX_I))

在样本较大时，极大似然估计满足相合性、渐进有效性、渐进正太性。但是在样本观测少于100时，估计的风险会比较大，大于100可以介绍大于500则更加充分。

模型评价

这里介绍拟合优度的评价的两个标准：AIC准则和SC准则，两统计量越小说明模型拟合的越好，越可信。

若事件发生的观测有n条，时间不发生的观测有M条，则称该数据有n*m个观测数据对，

在一个观测数据对中，P>1-P，则为和谐对（concordant）。P<1-P,则为不和谐对（discordant）。P=1-P，则称为结。

在预测准确性有一个统计量C=(NC-0.5ND+0.5T)/T，其中NC为和谐对数，ND为不和谐对数，这里我们就可以根据C统计量来表明模型的区分度，例如C=0.68，则表示事件发生的概率比不发生的概率大的可能性为0.68。

使用假设条件

①数据来自随机样本

②共线性敏感，自变量之间是非线性关系

③因变量只能取0、1

接下来看案例

PROC LOGISTIC DATA=EX.LOAN PLOTS(ONLY)=(EFFECT(CLBAND X=(DELINQ DEBTINC REASON))
                    ODDSRATIO (TYPE=HORIZONTALSTAT RANGE=CLIP));
    CLASS EDUCATION(REF="college") REASON(REF="car")/PARAM=REFERENCE;
    MODEL BAD(EVENT="")=DELINQ DEBTINC YROPEN EDUCATION REASON DELINQ*DEBTINC DEBTINC*EDUCATION/CLODDS=PL STB PARMLABEL;
    UNITS DEBTINC= -;
    ODDSRATIO EDUCATION/DIFF=ALL CL=PL;
    ODDSRATIO REASON/DIFF=ALL CL=PL;
    TITLE "BAD LOAN MODEL";
RUN;

PROC LOGISTIC可以用的常见的选项是noprint 、plots、namelen=n 分别对应功能为：不打印结果、输出画图、变量名长度为N（20~200）。其中plots语句中有ONLY表明指输出接下来指定图形。

后面跟着个effect选项，括号中的自选项有CLBAND和showobs指定在图形中表明预测概率的置信区域和观测，后面还有子选项X=变量1 变量2.....表明画出多个自变量的预测效应图（假设其余变量都取均值，只考虑指定自变量的因变量预测情况）。这里指定了三个变量，就会输出三个预测效果图。注：因变量分类大于2则effect失效。

PROC LOGISTIC的选项ODDSRATIO，后面跟着两个子选项TYPE和range，type=horizontalstat表明图形有段显示发生比率和置信区间，range=clip表明图形横坐标的范围是计算到的最小发生比率到最大发生比率。

语句CLASS,选项PARAM=可以去三个值：EFFECT \REFERENCE\ORDINAL，分别对应了三种不同将一个自变量分解成K-1个新变量的不同取值方法（一个变量有K个水平第　　k个水平为参考水平！）三种方法的不同在于对参考水平变量取值分别去-1、0、按水平的升序取值（用于顺序变量）。

选项REF=‘’的作用为指定变量中的某个取值作为参考水平。

MODEL语句有且只能有一个。这里的因变量BAD后面跟着选项event=“1”表明bad值为1时代表事件发生，此模型是计算BAD=1发生的概率。然后等号后面跟着可能进入模型的自变量，其中还有两个交互的自变量，为了研究两个变量是否有交互作用。

model 后面跟着选项CLODDS=表示输出事件发生比率的执行区间（PL表示用剖面函数计算， wald表示根据wald检验计算，both表示两种方法都计算一遍）。

model后面的选项STB表示对输出标准化，此选项是针对不同变量的度量单位可能不一致作用的，标准化后能更加客观的对比不同变量对预测因变量的作用的大小。

model后面还有选项parmlabel表明为极大似然估计的表中输出标签。

UNITS语句：上代码中表示DEBTINNC的值增加或者减少5个单位时计算一次发生比率。（默认变化一个单位计算一次，变化非常微小，步长跨度大一些会更有意义）。

ODSSRATIO语句，计算某一自变量的水平相对于参考水平的发生比率，选项DIFF=ALL表示比较所有水平间的发生比率，DIFF=REF表明相对参考水平的发生比率。选项CL=WALD\PL\BOTH和上文中讲的一致。

一下是输出结果：

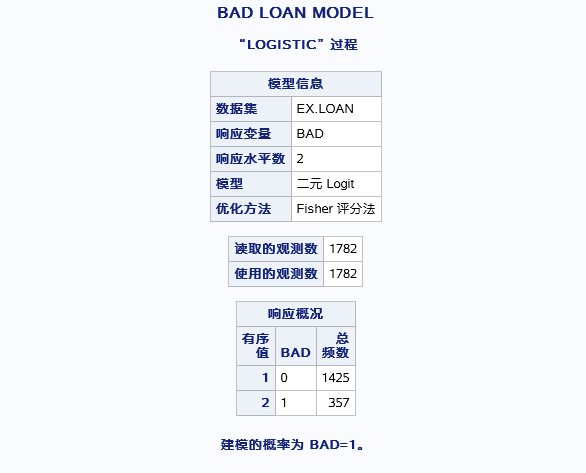
先输出一些基本情况，因变量水平数，观测数，以及频数，重要的是以什么条件建模（BAD=1）

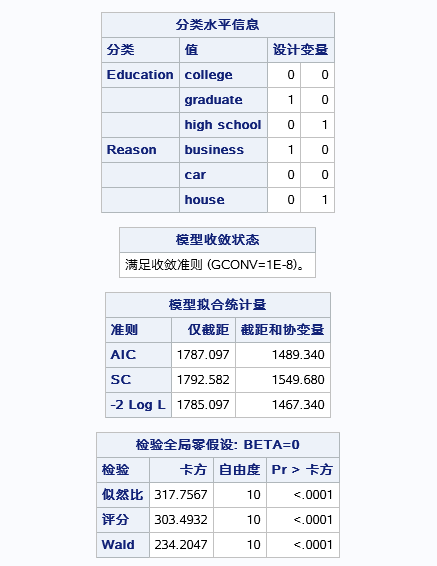
表一为根据两个变量的取不同水平，创建的新变量的取值

表二为模型的拟合优度判断，几个统计量是用于同一数据不同模型之间的比较才有意义，这里可以暂时忽略。

表三原假设为无线性关系（全局0假设），而根据三个统计量判断均是拒绝原假设，表示logit于自变量的线性关系显著。

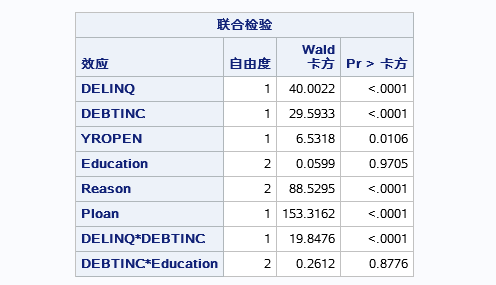
上表为变量的联合检验，也成为三效应检验，分别表示各个自变量对模型的显著性，即对因变量事件的发生有没有显著性。

以0.05的置信水平上有EDUCATION和DEBTINC*EDUCAION变量对模型没有显著性，其余的都有显著性。

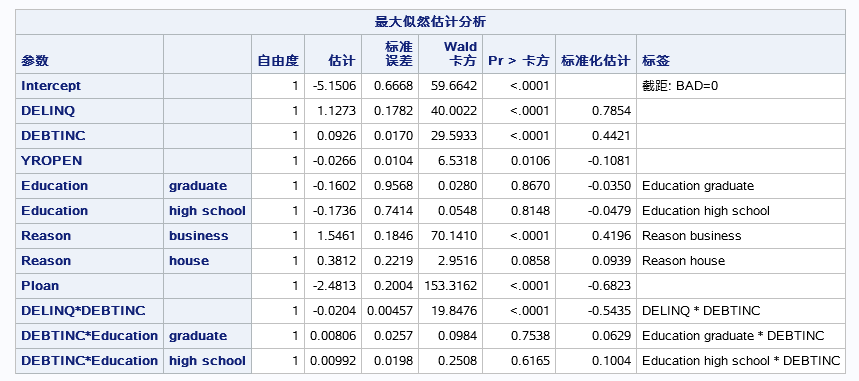
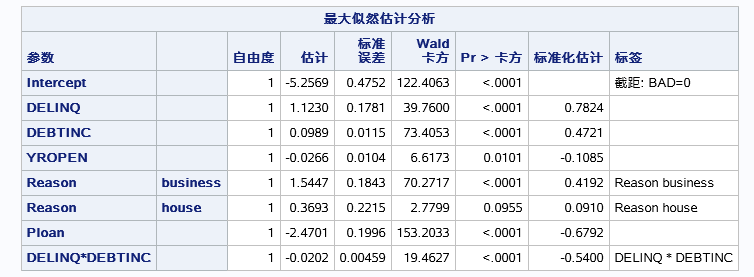
各个变量的参数估计包括截距的估计，还有标准化的参数估计（因为用了STB选项）。标准化后的估计值一般用来衡量不同自变量对因变量影响的大小（仅限于连续自变量，对于分类自变量标准化参数估计无意义）。还有一个统计量用于检查参数非零的显著性。

需要注意的是这里有两个变量EDUCATION和REASON的不同水平单独作为了一个变量进入模型。

注：以上是对所有变量都进行的参数估计，若在model后面再加一个选项SELECTION=FORWARD\BCKWARD\STEPWISE\SCORE指明一个模型选择法，则最终的结果就想之前的博客中一样，一步一步选择变量，最终得到一个类似于上表的表，区别在于不能进如模型的变量会不存在表中，如下图是向前选择的最终结果：

（一下为插入别的代码结果）

可见对变量进行筛选之后和不筛选是有区别的，一般认为筛选过的模型更加准确。

（以上为插入）

（以下为接着插入前的结果分析）

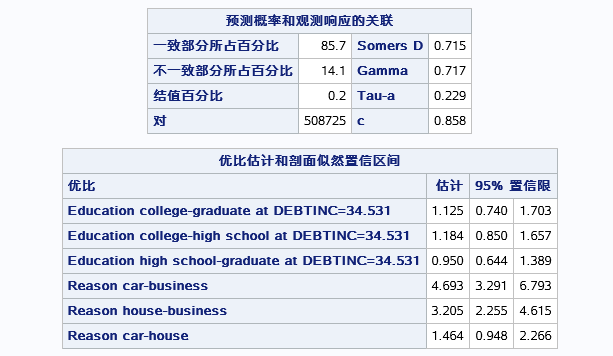
表一能衡量预测的准确性，一致部分的百分比即和观测于预测相同的占比有85.7，不一致的有14.1，不能确定的有0.2.。比较有价值的统计量是发生比率C=0.858，表明事件发生的概率比事件不发生的概率大的可能性有0.858。证明模型的有效。

表二，由于程序用了oddsratio语句，最用对象为EDUCATION和REASON，系统对两个变量的不同水平进行了求发生比率估计，即表二。前文说了发生比率不能等于1，而其中有两个新变量的置信区间包含了1，说明不同水平间对于发生比是无差别的，即新变量对发生不显著的。所以该模型中只有REASON 中BUSINESS和car两个水平的发生比是显著的，还有一个reason中house和business两水平的发生比是显著的。

还可以从图中看出相同结果：

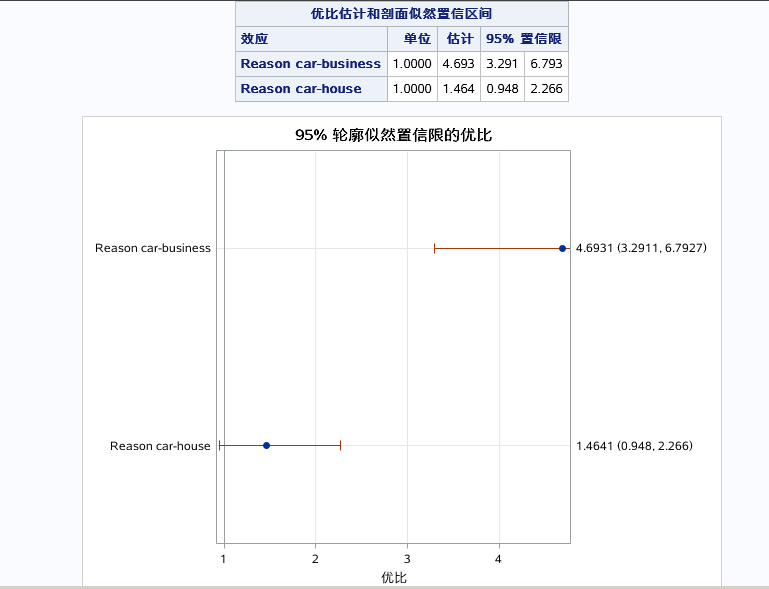
跟之前同理。

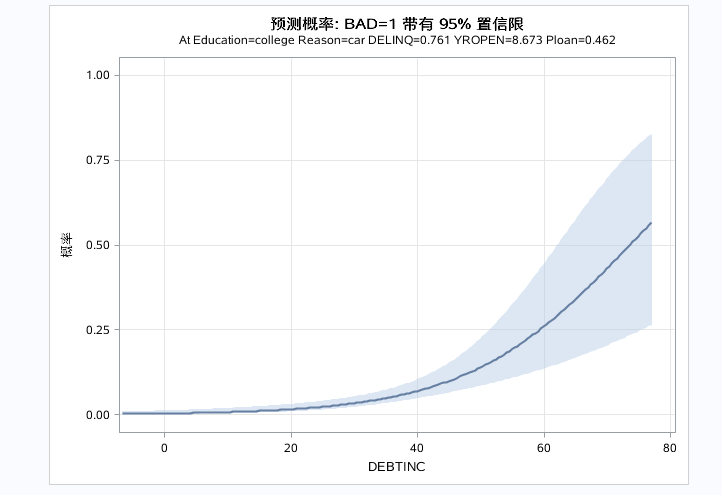
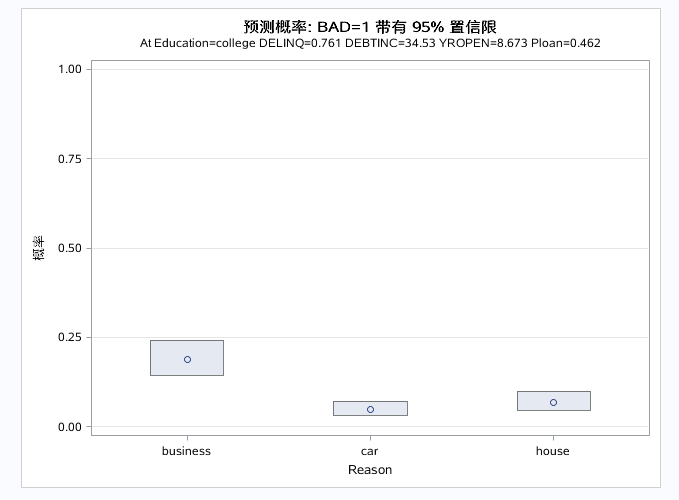
以上三图为自变量的预测效应图，分别控制别的自变量为均值或者参考水平是，单独看指定自变量和对因变量的预测效果。DEBTINC取值越大，预测概率越大。DELINQ取值越大，预测概率越大。对于分类变量得出business的预测概率最大。