【2(2N+1)魔方阵 】
/*
2(2N+1)魔方阵
*/ #include<stdio.h>
#include<stdlib.h> #define N 6
#define SWAP(x, y) {int t; t = x; x = y; y = t;} void magic_o(int [][N], int);
void exchange(int [][N], int); int main(void){
int square[N][N] = {};
int i, j;
magic_o(square, N/);
exchange(square, N); for(i = ; i < N; i++){
for( j = ; j < N; j++){
printf("%2d ", square[i][j]);
}
putchar('\n');
}
return ;
} void magic_o(int square[][N], int n){
int count, row, column;
row = ;
column = n /; for(count = ; count <= n*n; count++){
square[row][column] = count;
square[row+n][column+n] = count + n*n;
square[row][column+n] = count + *n*n;
square[row+n][column] = count + *n*n;
if(count % n == ){
row++;
}else{
row = (row == ) ? n - : row - ;
column = (column == n - ) ? : column + ;
}
}
} void exchange(int x[][N], int n){
int i, j;
int m = n / ;
int m1 = m - ; for(i = ; i < n/; i++){
if(i != m){
for(j = ; j < m; j++){
SWAP(x[i][j], x[n/+i][j]);
}
for(j = ; j < m1; j++){
SWAP(x[i][n--j], x[n/+i][n--j]);
}
}else{
for(j = ; j <= m; j++){
SWAP(x[m][j], x[n/+m][j]);
}
for(j = ; j <= m1; j++){
SWAP(x[m][n--j], x[n/+m][n--j]);
}
}
}
}
运行结果:
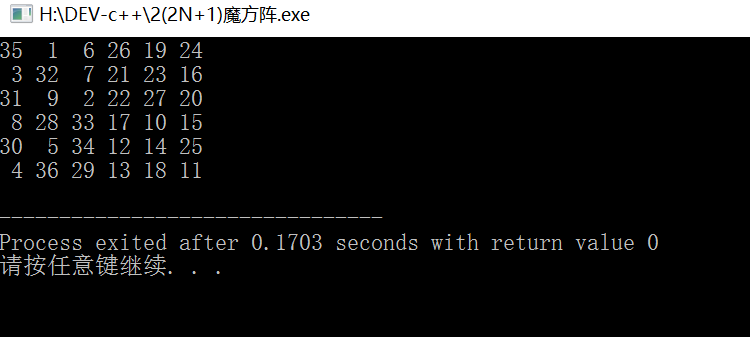
【2(2N+1)魔方阵 】的更多相关文章
- 任意阶魔方阵(幻方)的算法及C语言实现
写于2012.10: 本来这是谭浩强那本<C程序设计(第四版)>的一道课后习题,刚开始做得时候去网上找最优的算法,结果发现奇数和双偶数(4的倍数)的情况下算法都比较简单,但是单偶数(2的倍 ...
- 魔方阵算法及C语言实现
1 魔方阵概念 填充的,每一行.每一列.对角线之和均相等的方阵,阶数n = 3,4,5….魔方阵也称为幻方阵. 例如三阶魔方阵为: 魔方阵有什么的规律呢? 魔方阵分为奇幻方和偶幻方.而偶幻方又分为是4 ...
- C语言——打印魔方阵(每一行,每一列,对角线之和相等)
<一>魔方阵说明: 魔方阵是一个N*N的矩阵: 该矩阵每一行,每一列,对角线之和都相等: <二>魔方阵示例: 三阶魔方阵: 8 1 6 3 5 7 4 9 ...
- n阶魔方阵(奇数阵)的输出
需求 要求输出1~n²的自然数构成的魔方阵. STEP 1 什么是魔方阵? 魔方阵,古代又称“纵横图”,是指组成元素为自然数1.2…n2的平方的n×n的方阵,其中每个元素值都不相等,且每行.每列以及主 ...
- 神奇的魔方阵--(MagicSquare)(1)
本篇文章只对奇数阶以及偶数阶中阶数n = 4K的魔方阵进行讨论.下面就让我们进入正题: 1 :魔方阵的相关信息:(百度百科) https://baike.baidu.com/item/%E9%AD%9 ...
- 神奇的魔方阵--(MagicSquare)(2)
在上一篇博客中,我们讨论了阶数为奇数,以及阶数为(4K)的魔方阵的排列规则,以及代码实现(详见:https://www.cnblogs.com/1651472192-wz/p/14640903.htm ...
- node操作MongoDB数据库之插入
在上一篇中我们介绍了MongoDB的安装与配置,接下来的我们来看看在node中怎样操作MongoDB数据库. 在操作数据库之前,首先应该像关系型数据库一样建个数据库把... 启动数据库 利用命令提示符 ...
- c经典算法
1. 河内之塔 说明 河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时 北越的首都,即现在的胡志明市:1883年法国数学家 Ed ...
- Java经典算法大全
1.河内之塔.. 2.Algorithm Gossip: 费式数列. 3. 巴斯卡三角形 4.Algorithm Gossip: 三色棋 5.Algorithm Gossip: 老鼠走迷官(一) 6. ...
随机推荐
- [Unity Physics] Physics - Raycast
Class Variables类变量 gravity The gravity applied to all rigid bodies in the scene.场景中应用到所有刚性物体的重力. min ...
- UNITY3D中的文件存储管理
使用Path对象判断路径的完整性和正确性 using System; using System.IO; class Test { public static void Main() { string ...
- ISP和IAP
ISP(在系统编程)是一种不依赖于单片机自身软件的程序下载方式,特点是不需要从电路板上取下单片机,通过某种方式使单片机进入ISP模式,开放编程接口,由其使用的计算机将新的程序代码写入到存储器内.我们平 ...
- FZU 1064 教授的测试
递归构造答案. 根据当前整颗树的编号,可以计算左右子树有几个节点以及编号.因此,不断dfs下去就可以了. #include<cstdio> #include<cstring> ...
- Learning How to Learn, Part 1
Jan 8, 2015 • vancexu Learning How to Learn: Powerful mental tools to help you master tough subjects ...
- 关于浏览器和HTTP协议
关于浏览器 浏览器的主要功能就是向服务器发出请求,在浏览器窗口中展示想要访问的网络资源.这里资源一般是指 HTML 文档,图片等其他的类型.资源的位置由用户使用 URL(统一资源标示符)指定. 而浏览 ...
- 复习php的一些函数
2014.07.04 查看ecshop的一些源码,学习了一些函数.
- pku2104
传送门:http://poj.org/problem?id=2104 题目大意:给定一个长度为N的数组{A[i]},你的任务是解决Q个询问.每次询问在A[l], A[l+1], ...... , A[ ...
- partial类修饰符
partial是一个类修饰符,用于把类定义拆分为几个部分,便于代码管理,如class ClassA{void A(){;}void B(){;}}与partial class ClassA{void ...
- 使用Linux自定义自动补全命令完善自己的shell脚本
对于Linuxer来说,自动补全是再熟悉不过的一个功能了.当你在命令行敲下部分的命令时,肯定会本能地按下Tab键补全完整的命令,当然除了命令补全之外,还有文件名补全. Bash-completion ...
