UFLDL教程笔记及练习答案二（预处理：主成分分析和白化）

首先将本节主要内容记录下来。然后给出课后习题的答案。

笔记：

1：首先我想推导用SVD求解PCA的合理性。

PCA原理：如果样本数据X∈R^m×n。当中m是样本数量，n是样本的维数。PCA降维的目的就是为了使将数据样本由原来的n维减少到k维(k＜n)。方法是找数据随之变化的主轴，在Andrew
Ng的网易公开课上我们知道主方向就是X的协方差所相应的最大特征值所相应的特征向量的方向(前提是这里X在维度上已经进行了均值归一化)。

在matlab中我们通常能够用princomp函数来求解，具体见：http://blog.csdn.net/lu597203933/article/details/41544547。这里我们解说怎样用svd来求解。 我们的目的就是要求协方差矩阵所相应的特征值和特征向量。

神秘值分解求解：    

我们知道神秘值分解矩阵表示为：X =SVD^T，当中S是X*X^T的特征向量(R^m×m)。而V是对角矩阵(R^m×n)，每个对象值称为X的神秘值，是X*X^T或者X^T*X的特征值的非负平方根；D是X^T*X的特征向量(R^n×n)。当样本X在维度上进行了均值归一化，那么它的协方差就是：

因此D每一列都是协方差矩阵的的特征向量。因此X_pca=X*D就是PCA后的结果。

用上面对X进行神秘值分解求解协方差矩阵的特征向量(即数据随之变化的主方向)，全然是依据矩阵的神秘值分解定义得来的。可是存在这一个这种问题。当样本个数m很大时。我们须要的存储空间是m×m+m×n+n×n将会很大。那么我们有没有简便的方法呢。我们按例如以下公式求解

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvTHU1OTcyMDM5MzM=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="">

这里的sigma为协防差矩阵(R^n×n)。是对称半正定矩阵，依照神秘值分解的定义这里的S是sigma*sigma^T的特征向量。V为其sigma的神秘值，D为sigma^T*sigma的特征向量，也就是S的转置。以下我们证明这里的S也是X^T*X(X的协方差)的特征向量。V为协方差的特征值(有个倍数关系)。

由定义我们能够得知以下公式(大S和小s是区分开的；当中小d为协方差的特征向量，v为协方差特征值的非负平方根)

以下是推导过程：

我们能够看出小d就等于大S。也就是说sigma的神秘值分解得到的S就是我们要求的协方差(sigma)的特征向量。而m*V=v^Tv。得出sigma的神秘值正好是X的神秘值的平方(即为sigma的特征值)的倍数，这样也就能够通过前k个V个神秘值(即协方差的前k个特征值)所占的比重来决定k的大小。

因为sigma是Rn×n。与样本大小无关，因此我们通过对sigma进行神秘值分解间接得到协方差矩阵的特征向量和特征值所须要的存储空间为4*n*n。在样本数量非常大的时候，对空间要求将是大大的缩减。

因此我们通经常使用svd求解pca的代码例如以下：

avg = mean(X, 1);
X = X - repmat(avg, size(X,1),1);
sigma = X'*X./size(X,1);
[S,V,D]= svd(sigma);
Xpca = X*S;

结论：

[S,V,D^T]= svd(sigma)得到的S是X^TX(协方差)的特征向量。V是协方差的特征值矩阵，V也是X通过PCA后的数据的协方差矩阵，为对角矩阵。这样就表明去除了各个维度之间的相关性了。。

2：PCA白化和ZCA白化

在我们得到Xpca之后，它的协方差:

我们得出了PCA后数据的协方差就是原始数据协方差的特征值构成的矩阵V，故其为对角矩阵。除了对象元素，其他元素均为0，这说明其他维度之间没有相关性，即去除了数据之间的冗余。

PCA白化就是使PCA后数据(更准确的说是旋转之后的数据)的协方差变为单位矩阵，此时我们能够通过下面公式的得到。直接使用作为缩放因子来缩放每一个特征

考虑到特征值有可能为0，因此我们对其进行来正则化：

ZCA白化就是通过重构PCA白化后的原始数据，其协方差矩阵也是单位矩阵，非常多算法都是用白化作为预处理的步骤的，这样就去除了各个维度之间的相关性，得到对原始图像更低冗余的表示。

3：对图像数据应用PCA算法

这个在UFLDL教程有一小节，意思就是比方从图像中得到一个patch(14*14)，是一个196维的向量，我们须要做的是将这196维向量的均值归一化为0(无需做方差归一化)。可是注意这里和上面是有差别的，上面是对每个维度进行均值归一化。而这里是对每个样本进行均值归一化(我也不太理解为什么这样处理~~)，教程给出的理由是“对每个像素单独预计均值和方差意义不大。由于（理论上）图像任一部分的统计性质都应该和其他部分同样”这样就能保证全部的特征的均值在0附近。“依据应用。在大多数情况下，我们并不关注所输入图像的总体明亮程度。比方在对象识别任务中。图像的总体明亮程度并不会影响图像中存在的是什么物体。

更为正式地说，我们对图像块的平均亮度值不感兴趣，所以能够减去这个值来进行均值规整化”。

这样处理之后再对数据进行上述描写叙述的由svd求PCA后的数据及白化。

在进行 PCA/ZCA 白化时，首先使特征零均值化是非常有必要的。这保证了 。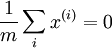

特别地。这一步须要在计算协方差矩阵前完毕。（唯一例外的情况是已经进行了逐样本均值消减，而且数据在各维度上或像素上是平稳的。）

练习答案：

须要注意的是下面联系的X是n×m维的。1 exercise：pca in 2D是对数据的维度进行均值归一化。。而2： Exercise:PCA and Whitening是对每个样本进行均值归一化(对图像的应用)

1： Exercise:PCA in 2D

(1)% Step 1a: Implement PCA to obtain U

u = zeros(size(x, 1)); % You need to compute this
avg = mean(x,2);     %按行求取均值
x = x - repmat(avg, 1,size(x,2));   %% size(x,2) = 45
sigma = x * x'/ size(x,2);
[u, s, v] = svd(sigma);

（2）Step 1b: Compute xRot, the projection on to the eigenbasis

xRot = u'* x;

(3)%% Step 2: Reduce the number ofdimensions from 2 to 1.

k = 1; % Use k = 1 and project the data onto the first eigenbasis
xHat = zeros(size(x)); % You need to compute this
x_ap = u(:,1:k)'*x;
xHat(1:k,:) = x_ap;
xHat = u*xHat;

(4)%% Step 3: PCA Whitening

xPCAWhite = diag(1./sqrt(diag(s) + epsilon)) * u' * x;

(5) %% Step 3: ZCA Whitening

xZCAWhite = u*diag(1./sqrt(diag(s) + epsilon)) * u' * x;

2： Exercise:PCA and Whitening

(1)% Step 0b: Zero-mean the data (byrow)

avg = mean(x, 1);
x = x - repmat(avg, size(x,1), 1);

(2)% Step 1a: Implement PCA to obtainxRot

xRot = zeros(size(x)); % You need to compute this
sigma = x*x'./size(x, 2);
[U,S,V] = svd(sigma);
xRot = U'*x;

(3)Step 1b: Check your implementationof PCA

covar = zeros(size(x, 1)); % You need to compute this
covar = xRot*xRot'/size(xRot,2);

（4）Step 2: Find k, the number of components to retain

k = 0; % Set k accordingly
sum_k = 0;
sum = trace(S);
for k = 1:size(S,1)
    sum_k = sum_k + S(k,k);
    if(sum_k/sum >= 0.99)
        break;
    end
end

（5）%% Step 3: Implement PCA with dimension reduction

xHat = zeros(size(x));  % You need to compute this                %%%%% 还原近似数据
xTilde = U(:,1:k)' * x;
xHat(1:k,:)=xTilde;
xHat=U*xHat;

(6)%% Step 4a: Implement PCA withwhitening and regularisation

xPCAWhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

(7)  % Step 4b: Check yourimplementation of PCA whitening

  covar = xPCAWhite * xPCAWhite'./size(xPCAWhite, 2);

(8)Step 5: Implement ZCA whitening

xZCAWhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;