Python - 八大排序算法
1、序言
本文使用Python实现了一些常用的排序方法。文章结构如下：
1.直接插入排序
2.希尔排序
3.冒泡排序
4.快速排序
5.简单选择排序
6.堆排序
7.归并排序
8.基数排序
上述所有的排序均写在一个Python自定义类中，作为成员函数。
2、排序方法详细介绍
1.直接插入排序
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，它的基本操作是一个值插入到已排好序的有序表中，从而得到一个新的、记录数增1的有序表。如下图所示：
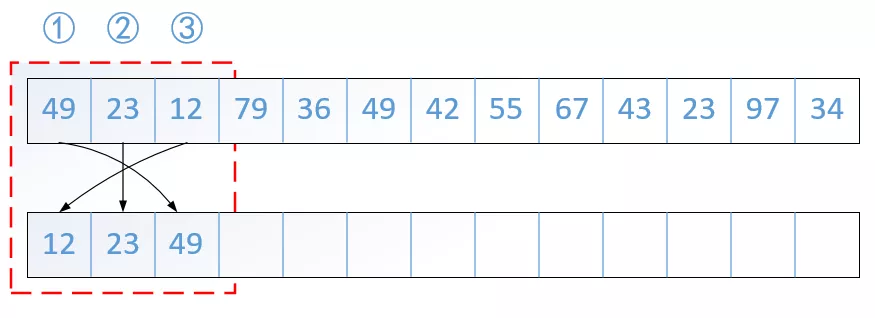
由上图可知若最初始的有序表即为数组的第一个元素。用Python实现如下：
def straight_insertion_sort(self, value_list):
"""
直接插入排序
:param value_list: 无序列表
:return:
"""
return self.__straight_insert(value_list) @staticmethod
def __straight_insert(value_list):
sorted_list = []
sorted_list.append(value_list.pop(0))
for i in range(0, len(value_list)):
tail = True # 是否在尾部插入
insert_loc = 0
for j in range(len(sorted_list)):
if value_list[i] <= sorted_list[j]:
tail = False
insert_loc = j
break
sorted_list.append(value_list[i]) # 先将值插入尾部
if not tail:
# 移动值
for j in range(len(sorted_list) - 1, insert_loc, -1):
temp = sorted_list[j]
sorted_list[j] = sorted_list[j - 1]
sorted_list[j - 1] = temp
return sorted_list
2.希尔排序
希尔排序（Shell’s Sort）又称“缩小增量排序”（Diminishing Incerement Sort），它也是一种数插入排序的方法，但在时间效率上较前面的排序方法有较大的改进。它的基本思想是：先将整个待排记录序列分割成若干个子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。如下图所示：
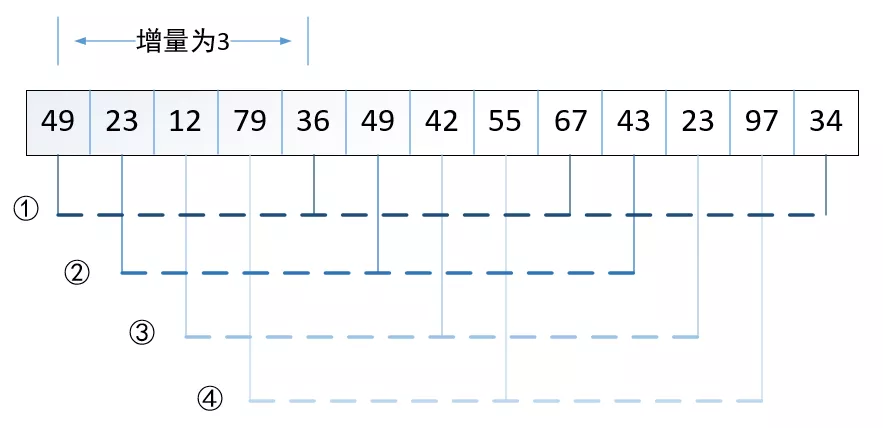
即根据增量将原序列分割成多个子序列进行直接插入排序。增量应不断减小，且最后一个增量为1。用Python实现如下：
def shells_sort(self, value_list):
"""
希尔排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
gap = len(value_list) // 2
while gap >= 1:
i = 0
while(i + gap) < len(value_list):
start = i
gap_list = []
while start < len(value_list):
gap_list.append(value_list[start])
start = start + gap
gap_list = self.__straight_insert(gap_list)
start = i
while start < len(value_list):
value_list[start] = gap_list.pop(0)
start += gap
i += 1
gap //= 2
sorted_list = value_list
return sorted_list
3.冒泡排序
冒泡排序（Bubble Sort）的过程很简单。首先将第一个记录的关键字和第二个记录的关键字进行比较，若逆序（与需要的顺序相反），则将两个记录交换之，然后比较第二个记录和第三个记录的关键字，以此类推。为第一趟冒泡结束，接着对前n-1个记录继续进行上述的过程。这样重复的过程直至n-1=1结束。排序过程如下所示：
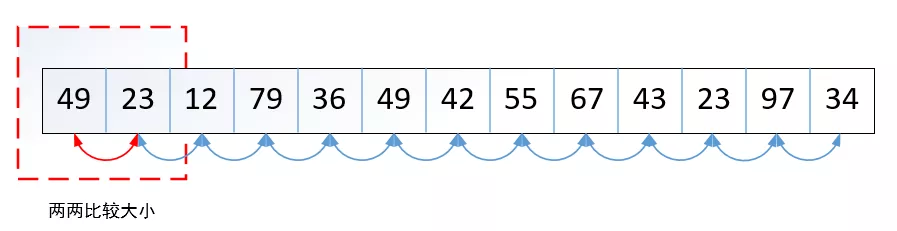
用Python实现如下：
@staticmethod
def bubble_sort(value_list):
"""
冒泡排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
for i in range(len(value_list) - 1):
for j in range(i + 1, len(value_list)):
if value_list[i] > value_list[j]:
value_list[i], value_list[j] = value_list[j], value_list[i]
sorted_list = value_list
return sorted_list
4.快速排序
快速排序（Quick Sort）是对冒泡排序的一种改进。它的基本思想是，通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，已达到整个序列有序。其排序思想如下：
首先任意选取一个记录（通常可选第一个记录）作为枢轴，然后按下述原则重新排列记录：将所有关键字较它小的记录都安置在它的位置之前，将所有关键字较它大的记录都安置在它的位置之后。一趟快速排序的具体做法是：设两个指针low和high，他们的初值分别为最低位置的下一个位置和最高位，设最低位置枢轴的关键字为pivotkey，则首先从high所指位置起向前搜索找到第一个关键字小于pivotkey的记录的枢轴记录互相交换。发生了交换后才从low所指向的位置起向后搜索，找到第一个关键字大于pivotkey的记录和枢轴记录互相交换。重复这两步直至low=how为止
如下图所示：
特别要注意换方向的时机是发生了交换后，用Python实现如下：
def quick_sort(self, value_list):
"""
快速排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
low = 0
high = len(value_list) - 1
self.__qsort(value_list, low, high)
sorted_list = value_list
return sorted_list def __qsort(self, val_list, low, high):
"""
快速排序辅助函数
:param val_list: 无序列表
:param low: 低位
:param high: 高位
:return:
"""
if low >= high:
return
pivot_key = low
temp_low = pivot_key
temp_high = high
while low < high:
# 分成一边比轴（pivot）大，一边比轴（pivot）小的顺序
while low < high:
if val_list[high] < val_list[pivot_key]:
temp = val_list[high]
val_list[high] = val_list[pivot_key]
val_list[pivot_key] = temp
pivot_key = high
break # 发生交换后，就换方向
else:
high -= 1
while low < high:
if val_list[low] > val_list[pivot_key]:
temp = val_list[low]
val_list[low] = val_list[pivot_key]
val_list[pivot_key] = temp
pivot_key = low
break # 发生交换后，就换方向
else:
low += 1
self.__qsort(val_list, temp_low, pivot_key - 1)
self.__qsort(val_list, pivot_key + 1, temp_high)
5.简单选择排序
选择排序（Selection Sort）是一种简单直观的排序算法。它的基本思想是：每一趟在n-i+1(i=1,2,...,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。简单选择排序：通过n-1次关键字的比较，从n-i+1个记录中选出关键字最小的记录，并和第i(1≤i≤n)个记录交换之。如下图所示：
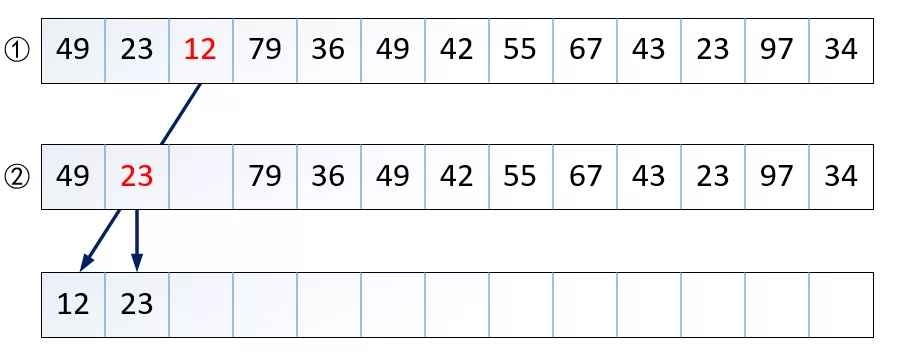
用Python实现如下：
@staticmethod
def simple_selection_sort(value_list):
"""
简单选择排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
for i in range(len(value_list)):
min_val = 9999999
for j in range(i, len(value_list)):
if min_val > value_list[j]:
min_val = value_list[j]
count = 0 # 如果有多个相同的最小值
for j in range(i, len(value_list)):
if min_val == value_list[j]:
value_list[j], value_list[i + count] = value_list[i + count], value_list[j]
sorted_list = value_list
return sorted_list
6.堆排序
堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆的定义如下：
n个元素的序列{k1,k2,...,kn}当且仅当满足一下关系时，称之为堆。
若将序列看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端节点均不大于（或不小于）其左、右孩子节点的值。由此，若序列是堆，则堆顶元素必为序列中的最小值（或最大值）。如下图所示：
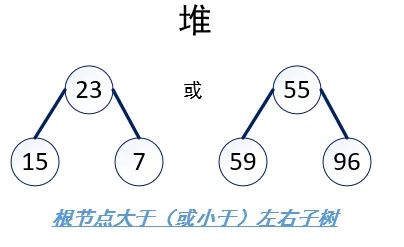
至此，我们可以给出堆排序的过程：若在输出堆顶的最小值后，使得剩余n-1个元素的序列又建成一个堆，则得到n个元素中的次小值。如此反复执行，便能得到一个有序序列。
故整个堆排序可以大致分为两个过程：
·将无序序列建成堆。
·输出堆顶元素后，用类似建堆的方法调整堆。
如下两个图所示：
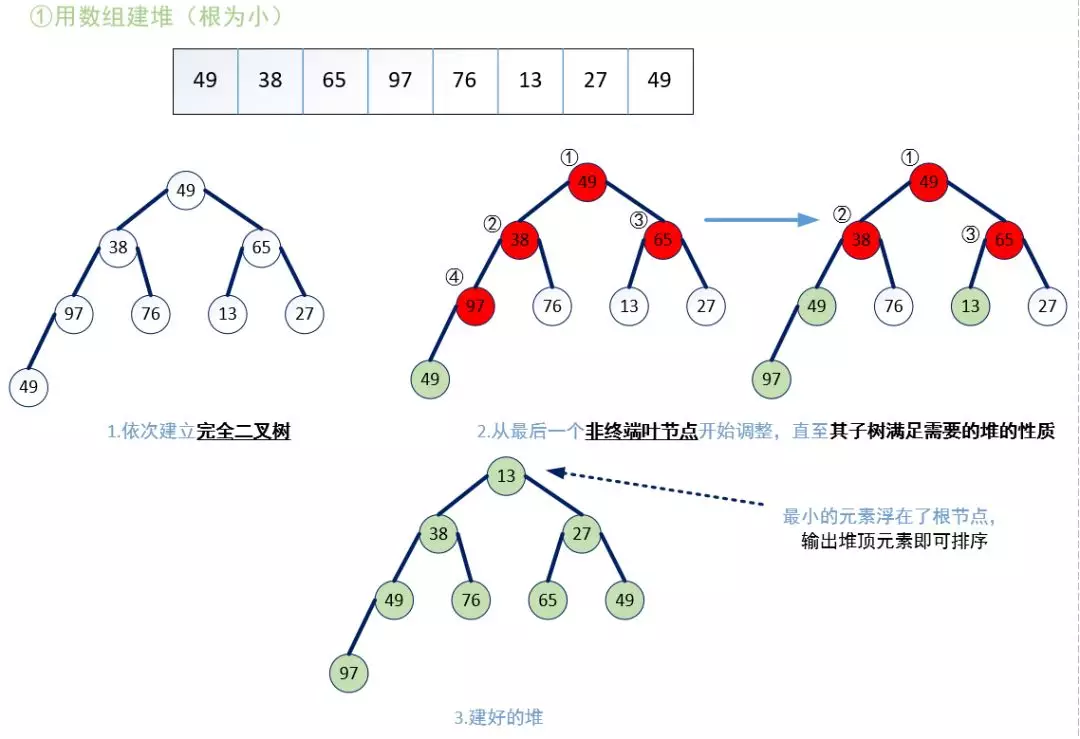
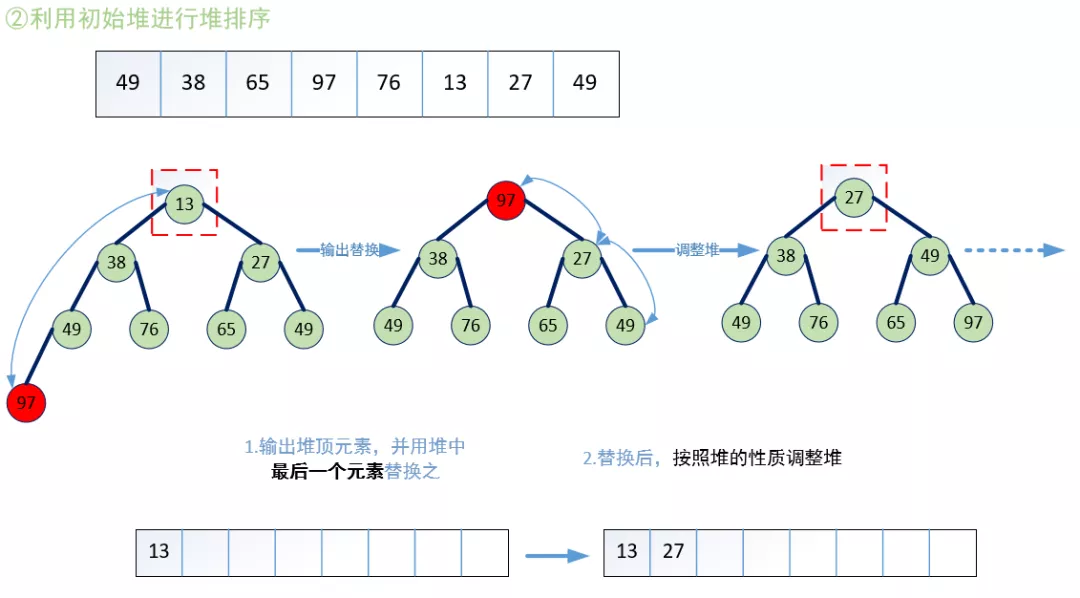
根据堆排序的特点总结出两点注意事项：
1.利用把堆看成完全二叉树的特点，用完全二叉树的性质解决算法问题。
2.建堆的过程是从树种的最后一个非终端节点逆序开始调整的。
3.每调整一次需要检查前后是否依然保持堆的特征。
本文利用了二叉树的孩子兄弟表示法来生成二叉树（堆）的。代码如下：
class CldSibNode(object):
"""
私有内部类：孩子兄弟二叉链表节点
""" def __init__(self, val):
self.value = val
self.child = None
self.sibling = None def heap_sort(self, value_list):
"""
堆排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
sorted_list = []
root_node = self.CldSibNode(None)
self.__child_sibling(root_node, value_list, 0)
for ct in range(1, len(value_list) // 2 + 1): # 建堆
self.__adjust_heap(root_node, len(value_list) // 2 + 1 - ct, 1)
for i in range(1, len(value_list) + 1): # 堆排序
sorted_list.append(root_node.value) # 输出堆顶元素
head = root_node
self.__shrink_heap(root_node, len(value_list) + 1 - i, 1, head)
self.__adjust_heap(root_node, 1, 1) # 调整堆 return sorted_list def __child_sibling(self, node, value_list, ind):
"""
创建完全二叉树的左孩子右兄弟二叉链表
:param node: 当前节点
:param value_list: 待排序的无序列表
:param ind:
:return:
"""
if ind >= len(value_list):
return
node.value = value_list[ind]
if ind * 2 + 1 < len(value_list):
node.child = self.CldSibNode(None) # 孩子
self.__child_sibling(node.child, value_list, ind * 2 + 1)
if ind * 2 + 2 < len(value_list):
node.child.sibling = self.CldSibNode(None) # 兄弟
self.__child_sibling(node.child.sibling, value_list, ind * 2 + 2) def __adjust_heap(self, root_node, last_ind, now_ind):
if not root_node or not root_node.child: # 不为空且有孩子
return
if now_ind == last_ind:
# 需要调整的非终端节点
temp = root_node
cg = False
while temp.child:
if temp.value > temp.child.value:
temp.value, temp.child.value = temp.child.value, temp.value
cg = True # 发生交换
if temp.child.sibling:
if temp.value > temp.child.sibling.value:
if cg:
# 如果发生过交换
temp.value, temp.child.value = temp.child.value, temp.value
temp.value, temp.child.sibling.value = temp.child.sibling.value, temp.value
temp = temp.child.sibling
continue
else:
if cg:
# 如果发生过交换
temp = temp.child
continue
break
# 递归
self.__adjust_heap(root_node.child, last_ind, now_ind * 2)
if root_node.child.sibling:
self.__adjust_heap(root_node.child.sibling, last_ind, now_ind * 2 + 1) def __shrink_heap(self, root_node, last_ind, now_ind, head):
if not root_node or now_ind * 2 > last_ind:
# 为空
return
if last_ind == now_ind * 2 + 1:
head.value = root_node.child.sibling.value
root_node.child.sibling = None
return True
if last_ind == now_ind * 2:
head.value = root_node.child.value
root_node.child = None
return True
if root_node.child:
self.__shrink_heap(root_node.child, last_ind, now_ind * 2, head)
self.__shrink_heap(root_node.child.sibling, last_ind, now_ind * 2 + 1, head)
7.归并排序
归并排序（Merging Sort），“归并”的含义是将两个或两个以上的有序表组合成一个新的有序表。假设初始序列有n个记录，则可看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到[n/2]个长度为2或1的有序子序列；再两两归并，……，如此重复，直至得到一个长度为n的有序序列为止，这种排序方法为2-路归并排序。算法的基本思想如下图所示：
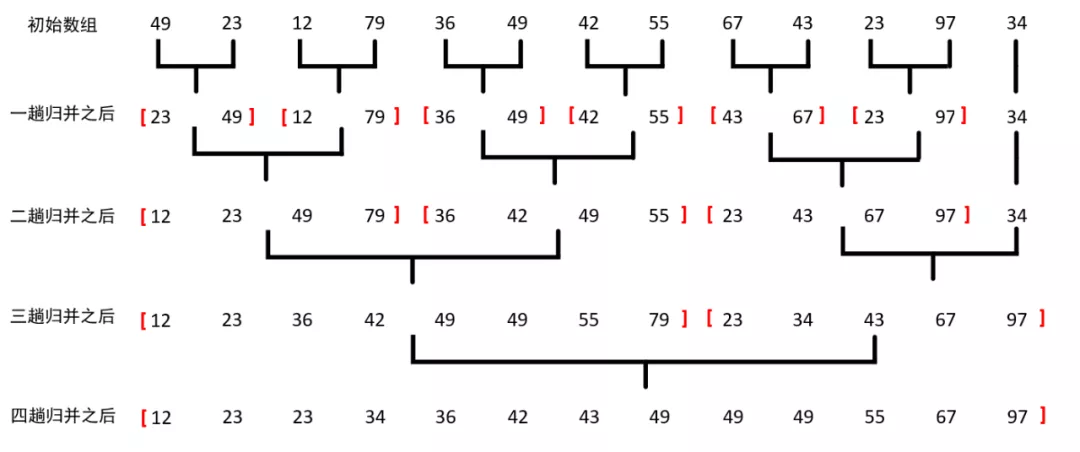
其中两个子序列的合并大有学问，基本思想就是：分别在两个序列头设置指针，比较两个序列指针所指的值的大小，将满足要求的值提取出来形成新列表，并将指针右移。当其中一个指针指向结尾之后时，表示其中一个列表已取尽，接着直接在新列表尾部连接另一个列表。如下图所示：
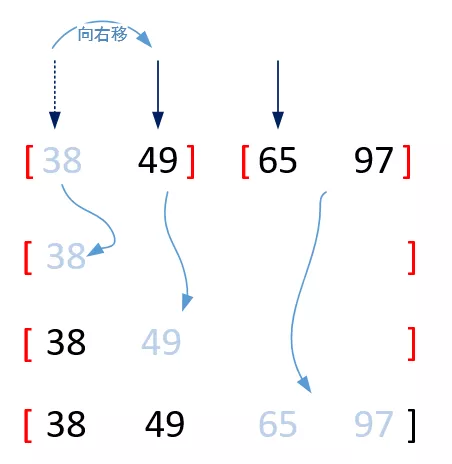
用Python实现如下：
@staticmethod
def merging_sort(self, value_list):
"""
归并排序
:param value_list: 待排序的无序列表
:return: 排序后的新列表
"""
i = 0
while np.power(2, i) < len(value_list):
count = np.power(2, i)
start = 0
outer_temp = []
while start < len(value_list):
# 定位另一边
other = start + count
temp = []
if other >= len(value_list):
# 另一边不存在：直接合并
outer_temp.extend(value_list[start: start + count])
break
left, right = 0, 0
while left < count or right < count:
if other + right >= len(value_list):
# 右边提前结束
temp.extend(value_list[start + left: start + count])
break
elif value_list[start + left] < value_list[other + right]:
# 左边更小
temp.append(value_list[start + left])
left += 1
if left == count:
# 左边遍历结束
temp.extend(value_list[other + right: other + count])
break
else:
# 右边更小
temp.append(value_list[other + right])
right += 1
if right == count:
# 右边遍历结束
temp.extend(value_list[start + left: start + count])
break
outer_temp.extend(temp)
start += count * 2
value_list = outer_temp
i += 1
sorted_list = value_list
return sorted_list
8.基数排序
基数排序（Radix Sort）是一种非比较整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。
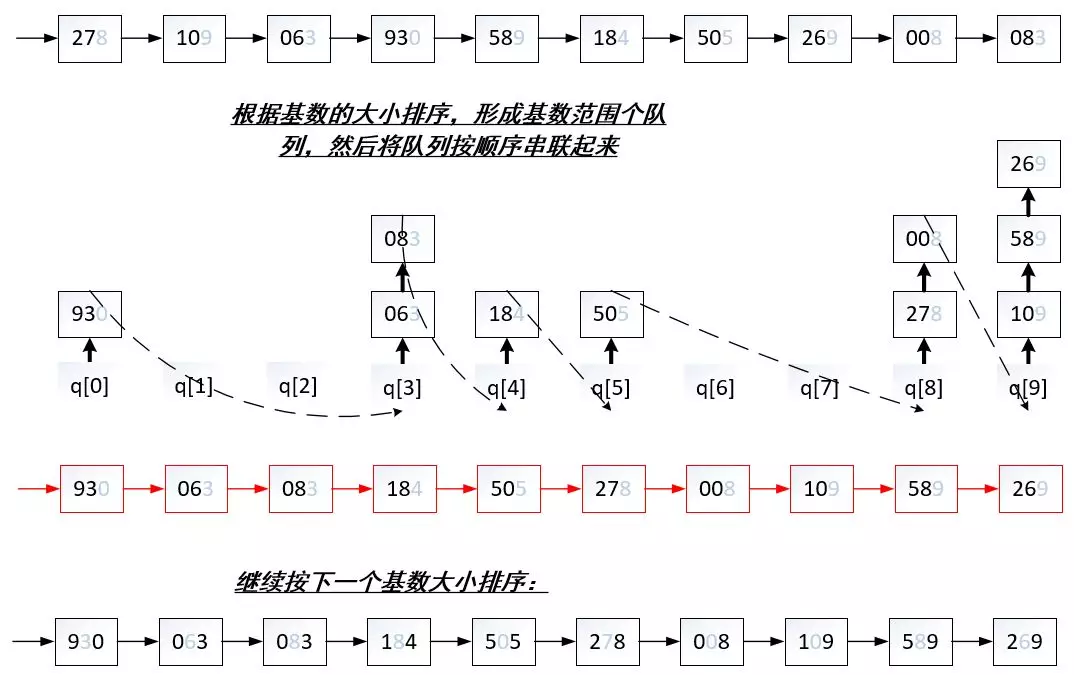
排序时有两点需要注意：
1.每完成一趟排序，要清空队列。
2.队列的连接要找到第一个不为空的队列作为头，和绕开所有空队列。
用Python实现如下：
@staticmethod
def radix_sort(value_list):
"""
基数排序
:param value_list: 待排序的无序列表
:return: 排序后的新列表
"""
i = 0
max_num = max(value_list)
n = len(str(max_num))
while i < n:
# 初始化桶数组
bucket_list = [[] for _ in range(10)]
for x in value_list:
# 找到位置放入桶数组
bucket_list[int(x / (10 ** i)) % 10].append(x)
value_list.clear()
for x in bucket_list:
# 放回原序列
for y in x:
value_list.append(y)
i += 1
sorted_list = value_list
return sorted_list
测试代码：
编写测试代码运行结果如下：
if __name__ == '__main__':
li = list(np.random.randint(1, 1000, 30))
my_sort = MySort()
print("original sequence:", li)
print("*" * 100)
print("1.straight_insertion_sort:", my_sort.straight_insertion_sort(li.copy()))
print("2.shells_sort:", my_sort.shells_sort(li.copy()))
print("3.bubble_sort:", my_sort.bubble_sort(li.copy()))
print("4.quick_sort:", my_sort.quick_sort(li.copy()))
print("5.simple_selection_sort:", my_sort.simple_selection_sort(li.copy()))
print("6.heap_sort:", my_sort.heap_sort(li.copy()))
print("7.merging_sort:", my_sort.merging_sort(li.copy()))
print("8.radix_sort:", my_sort.radix_sort(li.copy()))
测试运行结果：
original sequence: [424, 381, 234, 405, 554, 742, 527, 876, 27, 904, 169, 566, 854, 448, 65, 508, 226, 477, 12, 670, 408, 520, 774, 99, 159, 565, 393, 288, 149, 711]
****************************************************************************************************
1.straight_insertion_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
2.shells_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
3.bubble_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
4.quick_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
5.simple_selection_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
6.heap_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
7.merging_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
8.radix_sort: [12, 27, 65, 99, 149, 159, 169, 226, 234, 288, 381, 393, 405, 408, 424, 448, 477, 508, 520, 527, 554, 565, 566, 670, 711, 742, 774, 854, 876, 904]
总结
各个排序效率见下图：
可以得出以下几个结论：
1.从平均时间性能而言，快速排序最佳。
2.堆排序适用于n较大的数据。
3.基数排序是稳定的，时间复杂度较大的简单排序方法也是稳定的。
4.稳定性是由方法本身决定的。
5.没有最好的排序方法，视情况而定。
#! /usr/bin/env python3
# -*- coding:utf-8 -*- # Author : MaYi
# Blog : http://www.cnblogs.com/mayi0312/
# Date : 2020-01-06
# Name : mySort
# Software : PyCharm
# Note : 八大排序算法
import numpy as np class MySort(object):
"""
自定义一个排序的类
""" def straight_insertion_sort(self, value_list):
"""
直接插入排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
return self.__straight_insert(value_list) @staticmethod
def __straight_insert(value_list):
sorted_list = []
sorted_list.append(value_list.pop(0))
for i in range(0, len(value_list)):
tail = True # 是否在尾部插入
insert_loc = 0
for j in range(len(sorted_list)):
if value_list[i] <= sorted_list[j]:
tail = False
insert_loc = j
break
sorted_list.append(value_list[i]) # 先将值插入尾部
if not tail:
# 移动值
for j in range(len(sorted_list) - 1, insert_loc, -1):
sorted_list[j], sorted_list[j - 1] = sorted_list[j - 1], sorted_list[j]
return sorted_list def shells_sort(self, value_list):
"""
希尔排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
gap = len(value_list) // 2
while gap >= 1:
i = 0
while(i + gap) < len(value_list):
start = i
gap_list = []
while start < len(value_list):
gap_list.append(value_list[start])
start = start + gap
gap_list = self.__straight_insert(gap_list)
start = i
while start < len(value_list):
value_list[start] = gap_list.pop(0)
start += gap
i += 1
gap //= 2
sorted_list = value_list
return sorted_list @staticmethod
def bubble_sort(value_list):
"""
冒泡排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
for i in range(len(value_list) - 1):
for j in range(i + 1, len(value_list)):
if value_list[i] > value_list[j]:
value_list[i], value_list[j] = value_list[j], value_list[i]
sorted_list = value_list
return sorted_list def quick_sort(self, value_list):
"""
快速排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
low = 0
high = len(value_list) - 1
self.__qsort(value_list, low, high)
sorted_list = value_list
return sorted_list def __qsort(self, val_list, low, high):
"""
快速排序辅助函数
:param val_list: 无序列表
:param low: 低位
:param high: 高位
:return:
"""
if low >= high:
return
pivot_key = low
temp_low = pivot_key
temp_high = high
while low < high:
# 分成一边比轴（pivot）大，一边比轴（pivot）小的顺序
while low < high:
if val_list[high] < val_list[pivot_key]:
temp = val_list[high]
val_list[high] = val_list[pivot_key]
val_list[pivot_key] = temp
pivot_key = high
break # 发生交换后，就换方向
else:
high -= 1
while low < high:
if val_list[low] > val_list[pivot_key]:
temp = val_list[low]
val_list[low] = val_list[pivot_key]
val_list[pivot_key] = temp
pivot_key = low
break # 发生交换后，就换方向
else:
low += 1
self.__qsort(val_list, temp_low, pivot_key - 1)
self.__qsort(val_list, pivot_key + 1, temp_high) @staticmethod
def simple_selection_sort(value_list):
"""
简单选择排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
for i in range(len(value_list)):
min_val = 9999999
for j in range(i, len(value_list)):
if min_val > value_list[j]:
min_val = value_list[j]
count = 0 # 如果有多个相同的最小值
for j in range(i, len(value_list)):
if min_val == value_list[j]:
value_list[j], value_list[i + count] = value_list[i + count], value_list[j]
sorted_list = value_list
return sorted_list class CldSibNode(object):
"""
私有内部类：孩子兄弟二叉链表节点
""" def __init__(self, val):
self.value = val
self.child = None
self.sibling = None def heap_sort(self, value_list):
"""
堆排序
:param value_list: 待排序的无序列表
:return: 排序后的列表
"""
sorted_list = []
root_node = self.CldSibNode(None)
self.__child_sibling(root_node, value_list, 0)
for ct in range(1, len(value_list) // 2 + 1): # 建堆
self.__adjust_heap(root_node, len(value_list) // 2 + 1 - ct, 1)
for i in range(1, len(value_list) + 1): # 堆排序
sorted_list.append(root_node.value) # 输出堆顶元素
head = root_node
self.__shrink_heap(root_node, len(value_list) + 1 - i, 1, head)
self.__adjust_heap(root_node, 1, 1) # 调整堆 return sorted_list def __child_sibling(self, node, value_list, ind):
"""
创建完全二叉树的左孩子右兄弟二叉链表
:param node: 当前节点
:param value_list: 待排序的无序列表
:param ind:
:return:
"""
if ind >= len(value_list):
return
node.value = value_list[ind]
if ind * 2 + 1 < len(value_list):
node.child = self.CldSibNode(None) # 孩子
self.__child_sibling(node.child, value_list, ind * 2 + 1)
if ind * 2 + 2 < len(value_list):
node.child.sibling = self.CldSibNode(None) # 兄弟
self.__child_sibling(node.child.sibling, value_list, ind * 2 + 2) def __adjust_heap(self, root_node, last_ind, now_ind):
if not root_node or not root_node.child: # 不为空且有孩子
return
if now_ind == last_ind:
# 需要调整的非终端节点
temp = root_node
cg = False
while temp.child:
if temp.value > temp.child.value:
temp.value, temp.child.value = temp.child.value, temp.value
cg = True # 发生交换
if temp.child.sibling:
if temp.value > temp.child.sibling.value:
if cg:
# 如果发生过交换
temp.value, temp.child.value = temp.child.value, temp.value
temp.value, temp.child.sibling.value = temp.child.sibling.value, temp.value
temp = temp.child.sibling
continue
else:
if cg:
# 如果发生过交换
temp = temp.child
continue
break
# 递归
self.__adjust_heap(root_node.child, last_ind, now_ind * 2)
if root_node.child.sibling:
self.__adjust_heap(root_node.child.sibling, last_ind, now_ind * 2 + 1) def __shrink_heap(self, root_node, last_ind, now_ind, head):
if not root_node or now_ind * 2 > last_ind:
# 为空
return
if last_ind == now_ind * 2 + 1:
head.value = root_node.child.sibling.value
root_node.child.sibling = None
return True
if last_ind == now_ind * 2:
head.value = root_node.child.value
root_node.child = None
return True
if root_node.child:
self.__shrink_heap(root_node.child, last_ind, now_ind * 2, head)
self.__shrink_heap(root_node.child.sibling, last_ind, now_ind * 2 + 1, head) @staticmethod
def merging_sort(value_list):
"""
归并排序
:param value_list: 待排序的无序列表
:return: 排序后的新列表
"""
i = 0
while np.power(2, i) < len(value_list):
count = np.power(2, i)
start = 0
outer_temp = []
while start < len(value_list):
# 定位另一边
other = start + count
temp = []
if other >= len(value_list):
# 另一边不存在：直接合并
outer_temp.extend(value_list[start: start + count])
break
left, right = 0, 0
while left < count or right < count:
if other + right >= len(value_list):
# 右边提前结束
temp.extend(value_list[start + left: start + count])
break
elif value_list[start + left] < value_list[other + right]:
# 左边更小
temp.append(value_list[start + left])
left += 1
if left == count:
# 左边遍历结束
temp.extend(value_list[other + right: other + count])
break
else:
# 右边更小
temp.append(value_list[other + right])
right += 1
if right == count:
# 右边遍历结束
temp.extend(value_list[start + left: start + count])
break
outer_temp.extend(temp)
start += count * 2
value_list = outer_temp
i += 1
sorted_list = value_list
return sorted_list @staticmethod
def radix_sort(value_list):
"""
基数排序
:param value_list: 待排序的无序列表
:return: 排序后的新列表
"""
i = 0
max_num = max(value_list)
n = len(str(max_num))
while i < n:
# 初始化桶数组
bucket_list = [[] for _ in range(10)]
for x in value_list:
# 找到位置放入桶数组
bucket_list[int(x / (10 ** i)) % 10].append(x)
value_list.clear()
for x in bucket_list:
# 放回原序列
for y in x:
value_list.append(y)
i += 1
sorted_list = value_list
return sorted_list if __name__ == '__main__':
li = list(np.random.randint(1, 1000, 30))
my_sort = MySort()
print("original sequence:", li)
print("*" * 100)
print("1.straight_insertion_sort:", my_sort.straight_insertion_sort(li.copy()))
print("2.shells_sort:", my_sort.shells_sort(li.copy()))
print("3.bubble_sort:", my_sort.bubble_sort(li.copy()))
print("4.quick_sort:", my_sort.quick_sort(li.copy()))
print("5.simple_selection_sort:", my_sort.simple_selection_sort(li.copy()))
print("6.heap_sort:", my_sort.heap_sort(li.copy()))
print("7.merging_sort:", my_sort.merging_sort(li.copy()))
print("8.radix_sort:", my_sort.radix_sort(li.copy()))
完整代码
Python - 八大排序算法的更多相关文章
- Python 八大排序算法速度比较
这篇文章并不是介绍排序算法原理的,纯粹是想比较一下各种排序算法在真实场景下的运行速度. 算法由 Python 实现,用到了一些语法糖,可能会和其他语言有些区别,仅当参考就好. 测试的数据是自动生成的, ...
- 八大排序算法的 Python 实现
转载: 八大排序算法的 Python 实现 本文用Python实现了插入排序.希尔排序.冒泡排序.快速排序.直接选择排序.堆排序.归并排序.基数排序. 1.插入排序 描述 插入排序的基本操作就是将一个 ...
- Python实现八大排序算法（转载）+ 桶排序（原创）
插入排序 核心思想 代码实现 希尔排序 核心思想 代码实现 冒泡排序 核心思想 代码实现 快速排序 核心思想 代码实现 直接选择排序 核心思想 代码实现 堆排序 核心思想 代码实现 归并排序 核心思想 ...
- 【Python】八大排序算法的比较
排序是数据处理比较核心的操作,八大排序算法分别是:直接插入排序.希尔排序.简单选择排序.堆排序.冒泡排序.快速排序.归并排序.基数排序 以下是排序图解: 直接插入排序 思想 直接插入排序是一种最简单的 ...
- 八大排序算法总结与java实现（转）
八大排序算法总结与Java实现 原文链接: 八大排序算法总结与java实现 - iTimeTraveler 概述 直接插入排序 希尔排序 简单选择排序 堆排序 冒泡排序 快速排序 归并排序 基数排序 ...
- [Data Structure & Algorithm] 八大排序算法
排序有内部排序和外部排序之分,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存.我们这里说的八大排序算法均为内部排序. 下图为排序 ...
- Python之排序算法：快速排序与冒泡排序
Python之排序算法:快速排序与冒泡排序 转载请注明源地址:http://www.cnblogs.com/funnyzpc/p/7828610.html 入坑(简称IT)这一行也有些年头了,但自老师 ...
- 八大排序算法Java实现
本文对常见的排序算法进行了总结. 常见排序算法如下: 直接插入排序 希尔排序 简单选择排序 堆排序 冒泡排序 快速排序 归并排序 基数排序 它们都属于内部排序,也就是只考虑数据量较小仅需要使用内存的排 ...
- python实现排序算法 时间复杂度、稳定性分析 冒泡排序、选择排序、插入排序、希尔排序
说到排序算法,就不得不提时间复杂度和稳定性! 其实一直对稳定性不是很理解,今天研究python实现排序算法的时候突然有了新的体会,一定要记录下来 稳定性: 稳定性指的是 当排序碰到两个相等数的时候,他 ...
随机推荐
- json字符串和object之间的相互转化
package asi; import java.util.ArrayList; import com.alibaba.fastjson.JSON; import com.alibaba.fastjs ...
- 初识eclipse-java
开始时会有工程的地址需要设置,最好将程序放在一个单独的文件夹中 有时候会用到外部的驱动程序,如excel等,就需要导入jar包 具体的请看下篇博客.
- Java-POJ1009-Edge Detection(未完成,有C++代码)
RLE编码,还不会,先搬运一下大佬的代码,理解之后再用Java自己实现 #include <map> #include <vector> #include <cstdli ...
- 19年7月份面试7家公司，整理的java面试题（答案自行百度解决，也是个学习的过程）
Dubbo与注册中心Zookeeper了解多少ConcurrentHashMap的原理 集合 HashMap 和 HashTable和ConcurrentHashMap的原理以及区别HashMap初始 ...
- Apache Kafka（七）- Kafka ElasticSearch Comsumer
Kafka ElasticSearch Consumer 对于Kafka Consumer,我们会写一个例子用于消费Kafka 数据传输到ElasticSearch. 1. 构造ElasticSear ...
- TCL create list from file
proc create_list {filename {prompt verbose} {opts "" }} { set list_return {} if {[file exi ...
- c++ google glog模块安装和基本使用（ubuntu）环境
1,如何安装 1 Git clone https://github.com/google/glog.git 2 cd glog 3 ./autogen.sh 4 ./configure --prefi ...
- @AliasFor 原理
用法: import org.springframework.core.annotation.AliasFor; import java.lang.annotation.*; @Target(El ...
- 吴裕雄 python 机器学习——集成学习随机森林RandomForestRegressor回归模型
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets,ensemble from sklear ...
- 【原】接口mock作用
1.前后端 接口定义完成 并发开工 2.测试拿到mock接口 编写用例 3.mock接口 模拟异常服务器返回值 500 404 4.mock接口 模拟数据 不修改线上数据库