图解leetcode279 —— 完全平方数

每道题附带动态示意图，提供java、python两种语言答案，力求提供leetcode最优解。

描述：

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.

示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

思路：

　　　　这道题的官方分类是【动态规划】，所以我们用动态规划的方法来解，动态规划最重要的是找到它的状态转移方程（即找出状态间的关系）。

　　除了状态转移方程，我们也可以用状态转移表的方法来解题，但是状态转移表只能解维度比较低题，比如著名的0-1背包问题，影响状态转移的决策只有两种，把物品放入背包、不把物品放入背包。所以很容易就可以画出一张二维的状态转移表，但是像今天我们要解决的这种问题，假如n=12，那么影响状态转移的决策至少就有三种，取1，取4，取9，人脑很难想像出多维的状态转移表，所以这里我们采用状态转移方程的方法来解。

状态转移方程推导：

函数f(n)为求组成n的完全平方数的最小个数(就是该题），所以f(12) = 3；f(13) = 2。

我们记做f(n) = m。n可以拆分为 n = d + k*k这种形式。

比如12 = 8 + 2*2，13 = 4 + 3*3，因为无论是12还是13都是完全平方数组成的，所以一定可以转换成这种形式。

f(n) = f(d) + f(k*k)，因为k*k是一个完全平方数，所以f(k*k) = 1

即f(n) = f(d) + 1，而由 n = d + k*k可得，d = n - k*k，所以上式可化为：

f(n) = f(n-k*k) + 1，（k*k < n）。

这就得出了状态转移方程：dp[i] = min(dp[i-j*j]+1, dp[i])，（j*j <= i）

这里和dp[i]取最小的原因是dp[i-j*j]+1可能不止一个值，取这些值中的最小值。

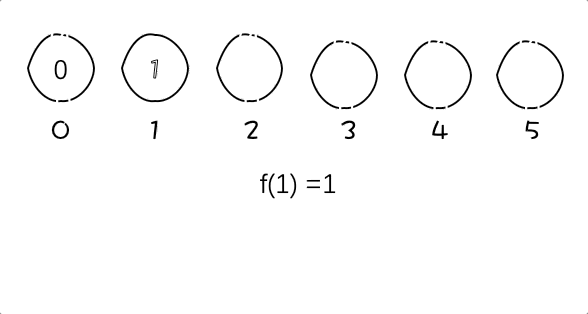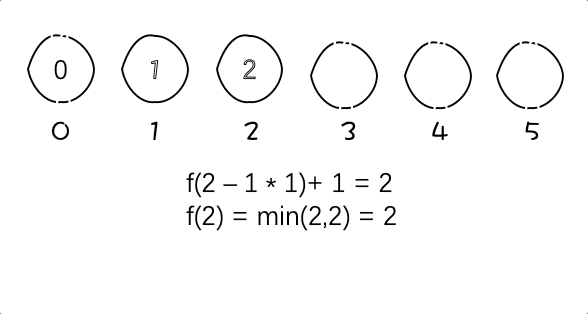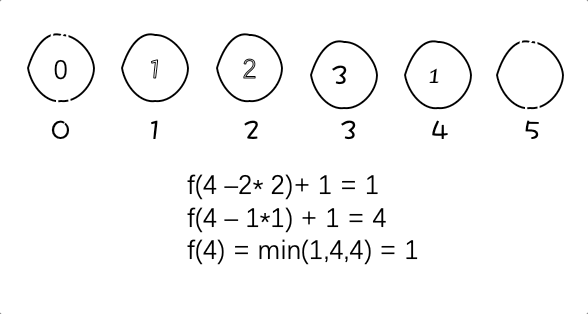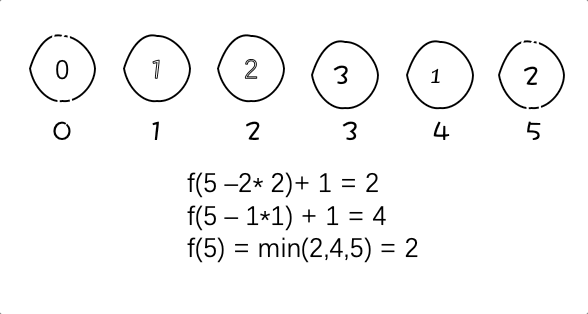
动图：

图中例子为f(5) = 2

5 = 4 + 1

实现：

java:

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        for (int i = 1; i < dp.length; i++) {
            dp[i] = i;
            for (int j = 1; i - j * j >= 0; j++) {
                dp[i] = Math.min(dp[i], dp[i - j * j]+1);
            }
        }
        return dp[n];
    }
}

结果：

python3:

class Solution:
    def numSquares(self, n: int) -> int:
        dp = [i for i in range(n + 1)]
        for i in range(1, n + 1):
            for j in range(1, n + 1):
                if i - j * j >= 0:
                    dp[i] = min(dp[i], dp[i - j * j] + 1)
                else:
                    break
        return dp[n]

结果：

期待您的关注、推荐、收藏，同时也期待您的纠错和批评，想看leetcode的其他题，可以在博客下方留言，每周都会更新。