ACM北大暑期课培训第七天

　　昨天没时间写，今天补下。

　　昨天学的强连通分支，桥和割点，基本的网络流算法以及Dinic算法：

　　强连通分支

　　定义：在有向图G中，如果任意两个不同的顶点 相互可达，则称该有向图是强连通的。 有向图G的极大强连通子图称为G的强连 通分支。

　　有向图强连通分支的Tarjan算法

　　做一遍DFS，用dfn[i]表示编号为i的节点在DFS过程中的访问序号(也可以叫做开始时间）。在DFS过程中会形成一搜索树。在搜索树上越先遍历到的节点，显然dfn的值就越小。dfn值越小的节点，就称为越“早” 。

　　用low[i]表示从i节点出发DFS过程中i下方节点(开始时间大 于dfn[i]，且由i可达的节点）所能到达的最早的节点的开始 时间。初始时low[i]=dfn[i]

　　DFS过程中，碰到哪个节点，就将哪个节点入栈。栈中节 点只有在其所属的强连通分量已经全部求出时，才会出栈。

　　如果发现某节点u有边连到栈里的节点v，则更新u的low值为min(low[u],dfn[v]) ，若low[u]被更新为dfn[v],则表明目前发现u可达的最早的节点是v。

　　如果一个节点u，从其出发进行的DFS已经全部完成并回到u，而且此时其low值等于dfn值，则说明u可达的所有节点，都不能到达任何比u早的节点 - --- 那么该节点u就是一个强连通分量在DFS搜索树中的根。  此时，显然栈中u上方的节点，都是不能到达比u 早的节点的。将栈中节点弹出，一直弹到u(包括u), 弹出的节点就构成了一个强连通分量。

///有向图强连通分支的Tarjan算法
///伪代码
void Tarjan(u)
{
    dfn[u]=low[u]=++index;
    stack.push(u);
    for each (u, v) in E
    {
        if (v is not visted)
        {
            Tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (v in stack)
        {
            low[u] = min(low[u], dfn[v])
        }
    }
    if (dfn[u] == low[u])   //u是一个强连通分量的根
    {
        repeat
        v = stack.pop
            print v
            until (u== v)
    } //退栈，把整个强连通分量都弹出来
} //复杂度是O(E+V)的

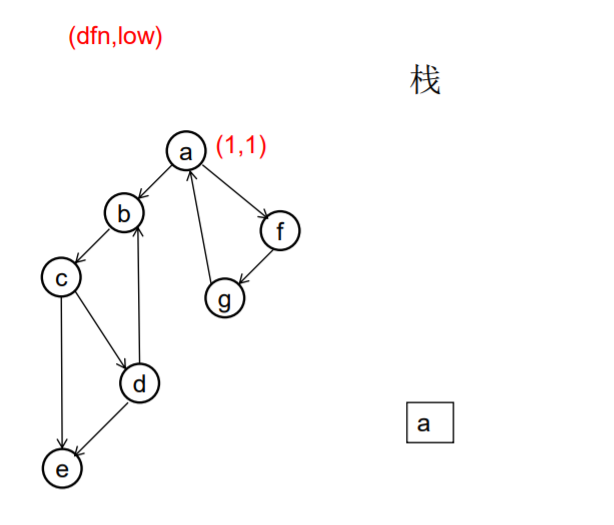
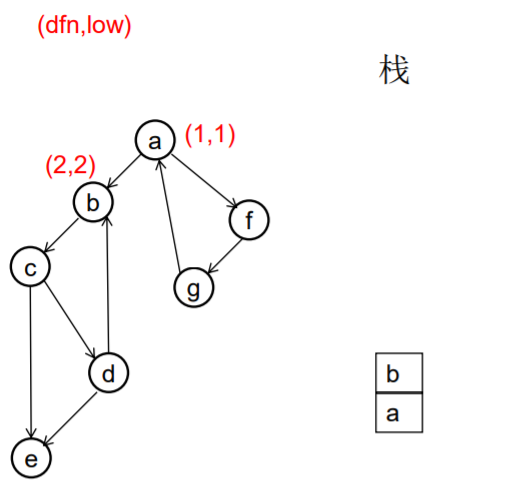
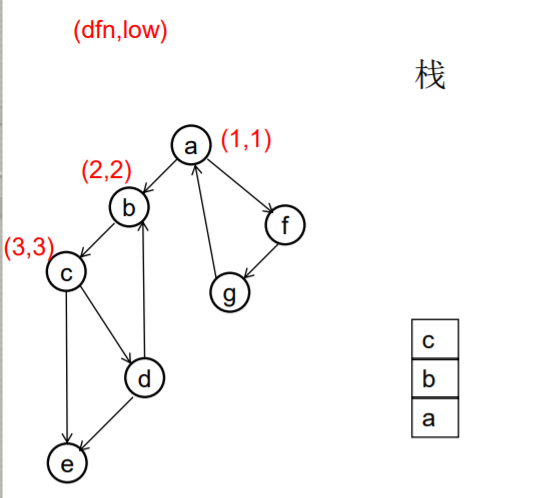
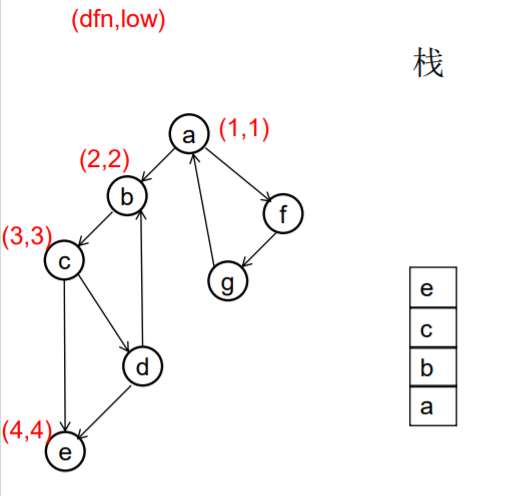
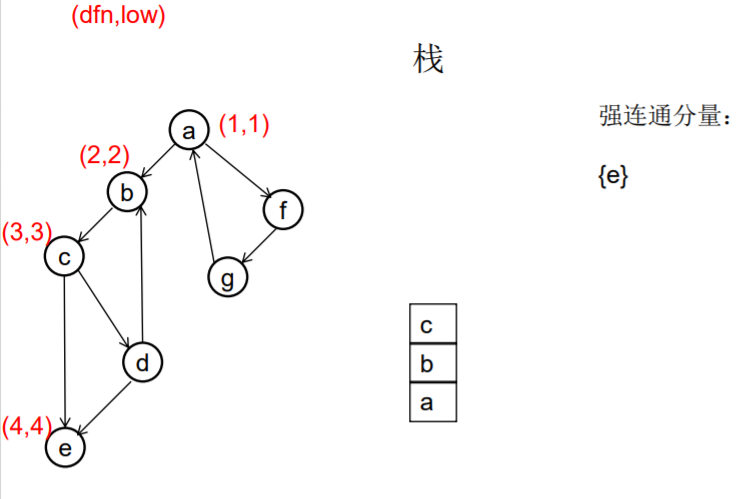
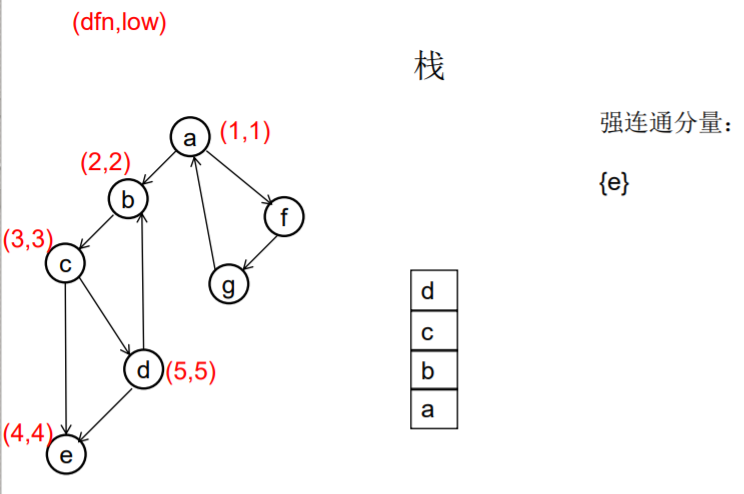
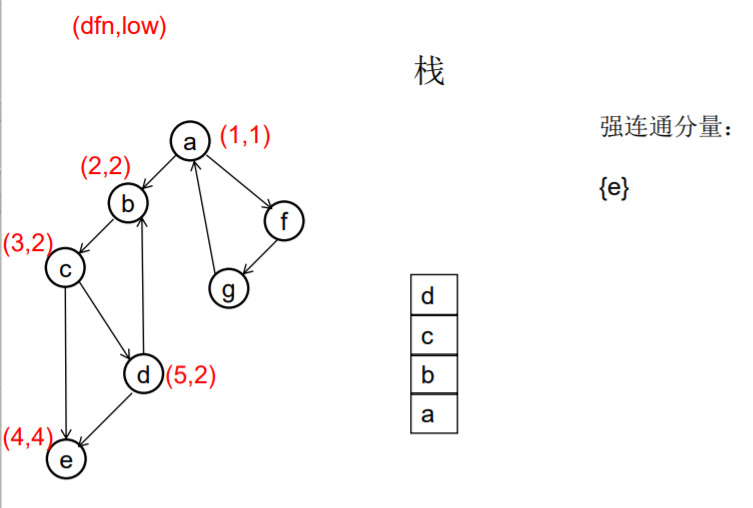
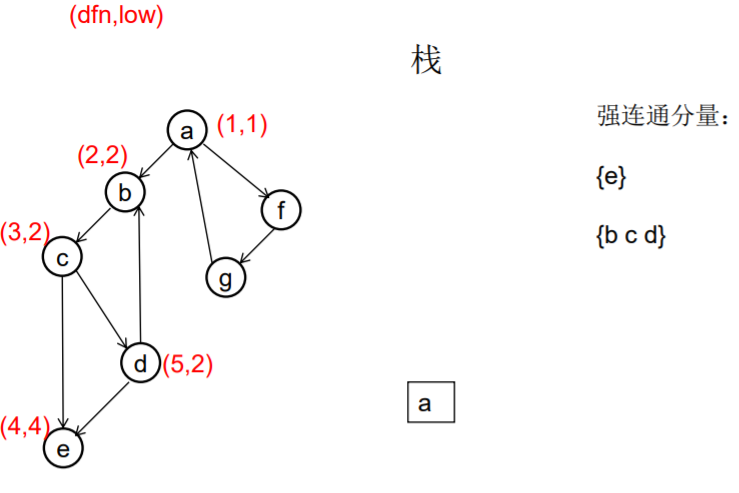
图示：

1.                                                                                                                    2.

                 

3.                                                                                                 4.

                             

5.                                                                                                                  6.

     

　　7.                                                                                                                       8.

          

　　9.                                                                                                                     10.

                     

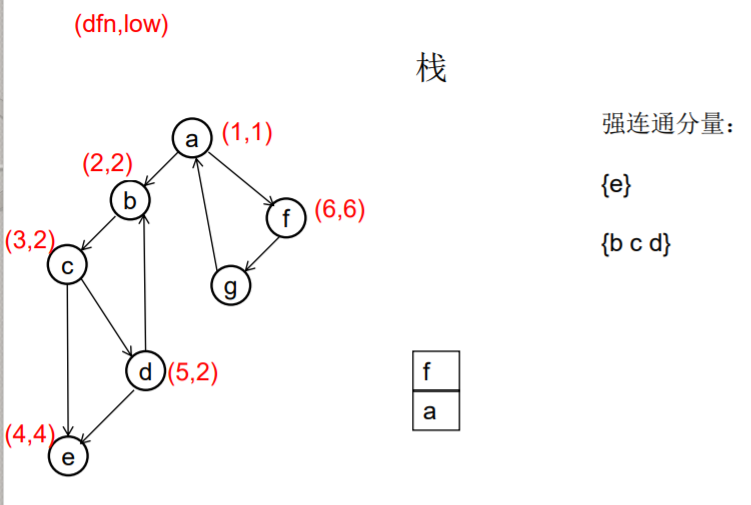
　　11.                                                                                                                     12.

                 

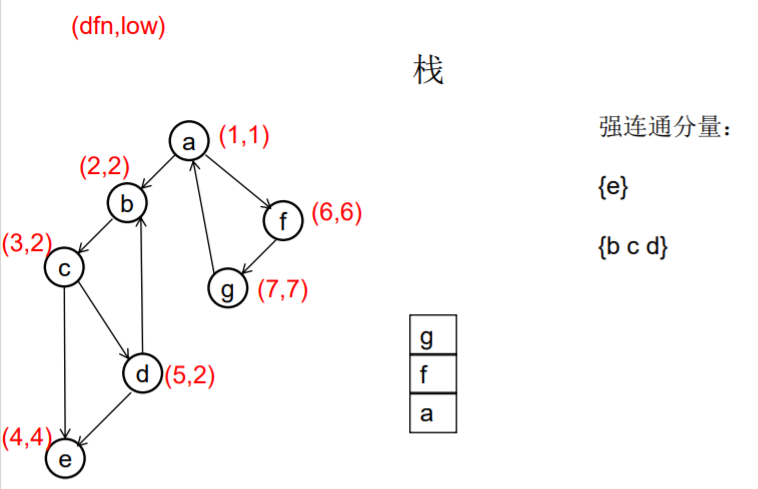
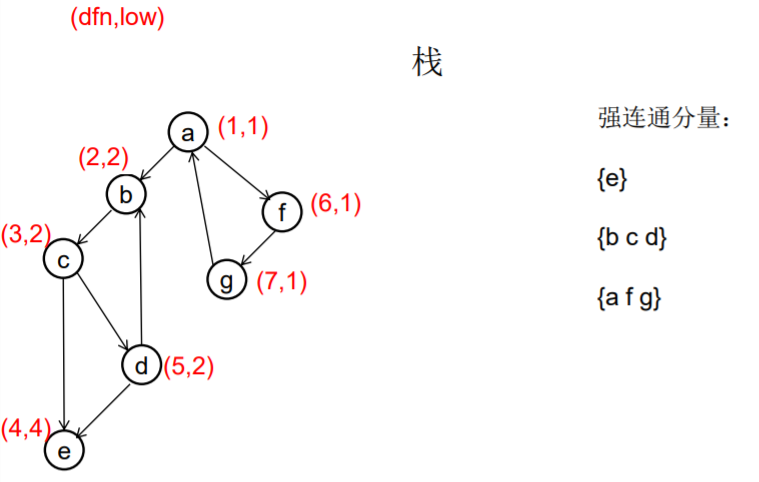
　　从u出发的DFS全部结束回到u时，若 dfn[u]=low[u], 此时将栈中u及其上方的节点 弹出，就找到了一个强连通分量

　　有用的定理:

　　1.有向无环图中唯一出度为0的点，一定可以由任何点出发均可达(由于无环，所以从任何点出发往前走，必然终止于一个出度为0的点)

　　2.有向无环图中所有入度不为0的点，一定 可以由某个入度为0的点出发可达。(由于无环，所以从任何入度不为0的点往回走，必然终止于一个入度为0的点)

例题：1.POJ 2186 Popular Cows

题目：
给定一个有向图，求有多少个顶点是由任何顶
点出发都可达的。
顶点数<= ,,边数 <= ,

思路：
. 求出所有强连通分量。
. 每个强连通分量缩成一点，则形成一个有向无环图DAG。
. DAG上面如果有唯一的出度为0的点,则该点能被所有的点可达。那么该点所代表的连通分量上的所有的原图中的点，都能被原图中的所有点可达，则该连通分量的点数，就是答案。
. DAG上面如果有不止一个出度为0的点，则这些点互相不可达，原问题无解，答案为0。

缩点的时候不一定要构造新图，只要把不同强连通分量的点染不同颜色，然后考察各种颜色的点有没有连到别的颜色的边即可(即其对应的缩点后的DAG图上的点是否有出边）。

题目+思路

　　　2.POJ 1236 Network of Schools

题目大意：
N(<N<)各学校之间有单向的网络，每个学校得到一套软件后，可以通过单向网络向周边的学校传输
问题
：初始至少需要向多少个学校发放软件，使得网络内所有的学校最终都能得到软件。
，至少需要添加几条传输线路(边)，使任意向一个学校发放软件后，经过若干次传送，网络内所有的学校最终都能得到软件。

给定一个有向图，求：
) 至少要选几个顶点，才能做到从这些顶点出
发，可以到达全部顶点
) 至少要加多少条边，才能使得从任何一个顶
点出发，都能到达全部顶点
   顶点数<= 

思路：
. 求出所有强连通分量
. 每个强连通分量缩成一点，则形成一个有向无环图DAG。
. DAG上面有多少个入度为0的顶点，问题1的答案就是多少

在DAG上要加几条边，才能使得DAG变成强连通的，问题2的答案就是多少
加边的方法：
    要为每个入度为0的点添加入边，为每个出度为0的点添加出边
    假定有 n 个入度为0的点，m个出度为0的点，max(m,n)就是第二个问题的解

题目+思路

　　无向连通图求割点和桥

　　割点：无向连通图中，如果删除某点后，图变 成不连通，则称该点为割点。

　 　桥    ：无向连通图中，如果删除某边后，图变 成不连通，则称该边为桥。

　　

　　求桥和割点的Tarjan算法： 思路和有向图求强连通分量类似

　　　　在深度优先遍历整个图过程中形成的一棵搜索树

　　　　dfn[u]定义和前面类似，但是low[u]定义为u或者u的子树中能够通过非父子边(父子边就是搜索树上的边）追溯到的最早的节点的DFS开始时间

　　求桥和割点的Tarjan算法：

　　如果下面程序没有： if(v 不是u 的父节点)    则求不出桥了

///伪代码
Tarjan(u)
{
    d[u]=low[u]=++index
    for each (u, v) in E
    {
        if (v is not visted)
            tarjan(v)
            low[u] = min(low[u], low[v])
            d[u]<low[v] <==> (u, v) 是桥
        }
    else
    {
        if(v 不是u 的父节点)
            low[u] = min(low[u], d[v])
        }
}
if (u is root)
    u 是割点 <=> u 有至少两个子节点
    else
        u 是割点 <=> u 有一个子节点v，满足d[u]<= low[v]
    }

求桥和割点和桥的Tarjan算法

　　也可以先用Tajan()进行dfs算出所有点 的low和dfn值，并记录dfs过程中每个点的父节点，然后再把所有点看一遍， 看其low和dfn,以找出割点和桥。

　　找桥的时候，要注意看有没有重边。有重边，则不是桥。

 //无重边连通无向图求割点和桥的程序

 /*
 题目：
 无重边连通无向图求割点和桥的程序
 给出点数和所有的边，求割点和桥
 Input: （11点13边）
 11 13
 1 2
 1 4
 1 5
 1 6
 2 11
 2 3
 4 3
 4 9
 5 8
 5 7
 6 7
 7 10
 11 3
 output:
 1
 4
 5
 7
 5,8
 4,9
 7,10

 */

 #include <iostream>
 #include <vector>
 using namespace std;
 #define MyMax 200
 typedef vector<int> Edge;
 vector<Edge> G(MyMax);
 bool Visited[MyMax] ;
 int dfn[MyMax] ;
 int low[MyMax] ;
 int Father[MyMax]; //DFS树中每个点的父节点
 bool bIsCutVetext[MyMax]; //每个点是不是割点
 int nTime; //Dfs时间戳
 int n,m; //n是点数，m是边数
 void Tarjan(int u, int father) //father 是u的父节点
 {
     Father[u] = father;
     int i,j,k;
     low[u] = dfn[u] = nTime ++;
     for( i = ; i < G[u].size() ; i ++ )
     {
         int v = G[u][i];
         if( ! dfn[v])
         {
             Tarjan(v,u);
             low[u] = min(low[u],low[v]);
         }
         else if( father != v ) //连到父节点的回边不考虑，否则求不出桥
             low[u] = min(low[u],dfn[v]);
     }
 }
 void Count()
 {
     //计算割点和桥
     int nRootSons = ;
     int i;
     Tarjan(,);
     for( i = ; i <= n; i ++ )
     {
         int v = Father[i];
         if( v ==  )
             nRootSons ++; //DFS树中根节点有几个子树
         else
         {
             if( dfn[v] <= low[i])
                 bIsCutVetext[v] = true;
         }
     }
     if( nRootSons > )
         bIsCutVetext[] = true;
     for( i = ; i <= n; i ++ )
         if( bIsCutVetext[i] )
             cout << i << endl;
     for( i = ; i <= n; i ++)
     {
         int v = Father[i];
         if(v > && dfn[v] < low[i])
             cout << v << "," << i <<endl;
     }
 }
 int main()
 {
     int u,v;
     int i;
     nTime = ;
     cin >> n >> m ; //n是点数，m是边数
     for( i = ; i <= m; i ++ )
     {
         cin >> u >> v; //点编号从1开始
         G[v].push_back(u);
         G[u].push_back(v);
     }
     memset( dfn,,sizeof(dfn));
     memset( Father,,sizeof(Father));
     memset( bIsCutVetext,,sizeof(bIsCutVetext));
     Count();
     return ;
 }

无重边连通无向图求割点和桥的代码

　　求无向图连通图点双连通分支(不包含割点的极大连通子图）：

　　对于点双连通分支，实际上在求割点的过程中就能顺便把每个点双连通分支求出。建立 一个栈，存储当前双连通分支，在搜索图时 ，每找到一条树枝边或反向边(连到树中祖先的边），就把这条边加入栈中。如果遇到某树枝边（u,v) 满足dfn(u)<=low(v)，说明u是 一个割点，此时把边从栈顶一个个取出，直到遇到了边(u,v)，取出的这些边与其关联的点，组成一个点双连通分支。割点可以属于多个点双连通分支，其余点和每条边只属于且属于一个点双连通分支。

　  　

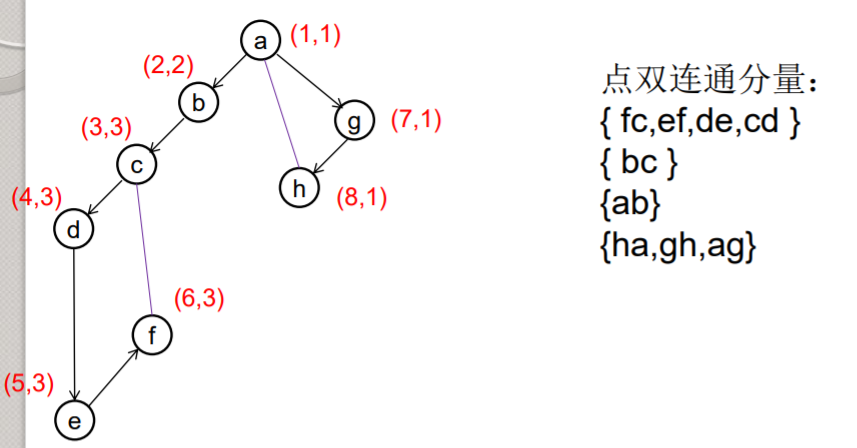
 ///求无向连通图点双连通分量（没有割点的连通分量）,假定没有重边

 /*
 Input: （8点9边）
 8 9
 1 2
 1 3
 1 5
 3 5
 2 4
 4 6
 4 7
 6 8
 7 8
 output:
 Block No: 1
 7,4
 8,7
 6,8
 4,6
 Block No: 2
 2,4
 Block No: 3
 1,2
 Block No: 4
 5,1
 3,5
 1,3
 */

 //求无向连通图点双连通分量（没有割点的连通分量）,假定没有重边
 #include <iostream>
 #include <cstring>
 #include <vector>
 #include <queue>
 using namespace std;
 #define MyMax 200
 typedef vector<int> Edge;
 vector<Edge> G(MyMax);
 int dfn[MyMax] ;
 int low[MyMax] ;
 int nTime;
 int n,m; //n是点数，m是边数
 struct Edge2
 {
     int u;
     int v;
     Edge2(int u_,int v_):u(u_),v(v_) { }
 };
 deque<Edge2> Edges; //栈
 int nBlockNo = ;
 void Tarjan(int u, int father)
 {
     int i,j,k;
     low[u] = dfn[u] = nTime ++;
     for( i = ; i < G[u].size() ; i ++ )
     {
         int v = G[u][i];
         if( ! dfn[v])   //v没有访问过
         {//树边要入栈
             Edges.push_back(Edge2(u,v));
             Tarjan(v,u);
             low[u] = min(low[u],low[v]);
             Edge2 tmp(,);
             if(dfn[u] <= low[v])
             {
 //从一条边往下走，走完后发现自己是割点，则栈中的边一定全是和自己在一个双连通分量里面
 //根节点总是和其下的某些点在同一个双连通分量里面
                 cout << "Block No: " << ++ nBlockNo<< endl;
                 do
                 {
                     tmp = Edges.back();
                     Edges.pop_back ();
                     cout << tmp.u << "," <<
                          tmp.v << endl;
                 }
                 while ( !(tmp.u == u &&
                           tmp.v == v) );
             }
         } // 对应if( ! dfn[v]) {
         else
         {
             if( v != father )  //u连到父节点的回边不考虑
             {
                 low[u] = min(low[u],dfn[v]);
                 if( dfn[u] > dfn[v])
 //连接到祖先的回边要入栈，但是连接到儿子的边，此处肯定已经入过栈了，不能再入栈
                     Edges.push_back(Edge2(u,v));
             }
         }
     } //对应 for( i = 0;i < G[u].size() ;i ++ ) {
 }
 int main()
 {
     int u,v;
     int i;
     nTime = ;
     cin >> n >> m ; //n是点数，m是边数
     nBlockNo = ;
     for( i = ; i <= m; i ++ )
     {
         cin >> u >> v; //点编号从1开始
         G[v].push_back(u);
         G[u].push_back(v);
     }
     memset( dfn,,sizeof(dfn));
     Tarjan(,);
     return ;
 }

例子

　　求无向连通图边双连通分支(不包 含桥的极大连通子图）： 　　

　　只需在求出所有的桥以后，把桥边删除，原图变成了多个连通块，则每个连通块就是一个边双连通分支。桥不属于任何一个边双连通分支，其余的边和每个顶点都属于且只属于 一个边双连通分支。

例题：POJ 3352 Road Construction

题目意思：
    给你一个图，要求你加入最少的边，使得最后得到的图为一个边双连通分支。所谓的边双连通分支，即不存在桥的连通分支。
    可以求出所有的桥，把桥删掉。然后把所有的连通分支求出来，显然这些连通分支就是原图中的双连通分支。把它们缩成点，然后添上刚才删去的桥，就构成了一棵树。在树上添边使得树变成一个双连通分支即可。
    本题只要求输出一共需要添加多少条边，而不需要求具体的方案。其实可以统计度为1的叶子节点（设共有x个），然后直接输出(x+)/2即可

命题：一棵有n(n>=)个叶子结点的树，至少(只需）要添加ceil(n/)条边，才(就)能转变为一个没有桥的图。或者说，使得图中每条边，都至少在一个环上。

证明：
这里只证明n为偶数的情况。n为奇数的证明类似。
先证明添加n/2条边一定可以达成目标。
n=2时，显然只需将这两个叶子间连一条边即可。命题成立。
设n=2k(k>=)时命题成立，即AddNum(2k)=k。下面将推出n=(k+)时命题亦成立
n=2k+2时，选取树中一条迹(无重复点的路径），设其端点为a,b；并设离a最近的度>=3的点为a',同理设b'。（关于a‘和b’的存在性问题：由于a和b的度都为1,因此树中其它的树枝必然从迹<a,b>之间的某些点引出。否则整棵树就是迹<a,b>，n=<2k+，不可能。）

a’ b’不重合时：
在a,b间添一条边，则迹<a,b>上的所有边都已不再是桥。这时，将刚才添加的边，以及aa‘之间，bb’之间的边都删去，得到一棵新的树。因为删去的那些边都已经符合条件了，所以在之后的构造中不需要考虑它们。由于之前a‘和b’的度>=，所以删除操作不会使他们变成叶子。因此新的树必然比原树少了两个叶子a,b，共有2k个叶子。由归纳知需要再加k条边。因此对n=2k+2的树，一共要添加k+1条边。

a’ b’ 重合时：
将a和一个非b的叶子节点x连上，然后将环缩点至 a’。因为叶子节点是偶数，所以必然还存在一个非b非x的叶子节点不在环上， 因此a’不会变成叶子节点，于是新图比原图少2个叶子节点。

再证明n/2是最小的解。
显然，只有一个叶子结点被新加的边覆盖到，才有可能使与它相接的那条边进入一个环中。而一次加边至多覆盖2个叶子。因此n个叶子至少要加n/2条边。
证毕。

讲解

　　其他题目：acm1236，acm3180，acm2762（强连通+拓扑排 序），acm2553，acm3114（强连通 +dijkstra), acm3160(强连通+DP）

　　网络流算法

　　网络流图里，源点流出的量，等于汇点流 入的量，除源汇外的任何点，其流入量之 和等于流出两之和

　　解决最大流的Ford-Fulkerson算法

　　求最大流的过程，就是不断找到一条源到汇的路径，然后构建残余网络，再在残余网络上寻找新的路径，使总流量增加，然后形成新的残余网络，再寻找新路径…..直到某个残余网络上找不到从源到汇的路径为止，最大流就算出来了。

　　每次寻找新流量并构造新残余网络的过程， 就叫做寻找流量的“增广路径”，也叫“增 广”

　　残余网络：在一个网络流图上，找到一条源到汇的路径（即找到了一个流量）后，对路径上所有的边，其容量都减去此次找到的流量，对路径 上所有的边，都添加一条反向边，其容量也 等于此次找到的流量，这样得到的新图，就称为原图的“残余网络”。

　　为什么添加反向边（取消流）是有效的？

　　假设在第一次寻找流的时候，发现在b->a上 可以有流量n来自源，到达b，再流出a后抵达汇点。

　　构建残余网络时添加反向边a->b，容量是n,增 广的时候发现了流量n-k，即新增了n-k的流量。 这n-k的流量，从a进，b出，最终流到汇

　　这2n-k的从流量，在原图上可以从源流到汇

　　现在假设每条边的容量都是整数

　　这个算法每次都能将流至少增加1

　　由于整个网络的流量最多不超过图中所有的边的容量和C，从而算法会结束

　　现在来看复杂度

　　找增广路径的算法可以用dfs， 复杂度为边数m+顶 点数n

　　Dfs 最多运行C次

　　所以时间复杂度为C*(m+n) =C* n²

　

　　为了避免C很大时程序要执行很多次的情况，在每次增广的时候，选择从源到汇的具有最 少边数的增广路径,即不是通过dfs寻找增广路 径，而是通过bfs寻找增广路径。这就是Edmonds-Karp最短增广路算法。已经证明这种算法的复杂度上限为nm²(n是点数，m是边数）。

例题：POJ 1273 Drainage Ditches

 /*
 题目：
 赤裸裸的网络流题目。给定点数，边数，每条
 边的容量，以及源点，汇点，求最大流。
 Sample Input
 5 4
 1 2 40
 1 4 20
 2 4 20
 2 3 30
 3 4 10
 Sample Output
 50
 */

 #include <cstring>
 #include <iostream>
 #include <queue>
 using namespace std;
 int G[][];
 int Prev[]; //路径上每个节点的前驱节点
 bool Visited[];
 int n,m; //m是顶点数目，顶点编号从1开始 1是源，m是汇, n是边数
 unsigned Augment()
 {
     int v;
     int i;
     deque<int> q;
     memset(Prev,,sizeof(Prev));
     memset(Visited,,sizeof(Visited));
     Prev[] = ;
     Visited[] = ;
     q.push_back();
     bool bFindPath = false;
 //用bfs寻找一条源到汇的可行路径
     while( ! q.empty())
     {
         v = q.front();
         q.pop_front();
         for( i = ; i <= m; i ++)
         {
             if( G[v][i] >  && Visited[i] == )
             {
 //必须是依然有容量的边，才可以走
                 Prev[i] = v;
                 Visited[i] = ;
                 if( i == m )
                 {
                     bFindPath = true;
                     q.clear();
                     break;
                 }
                 else
                     q.push_back(i);
             }
         }
     }
     if( ! bFindPath)
         return ;
     int nMinFlow = ;
     v = m;
 //寻找源到汇路径上容量最小的边，其容量就是此次增加的总流量
     while( Prev[v] )
     {
         nMinFlow = min( nMinFlow,G[Prev[v]][v]);
         v = Prev[v];
     }
 //沿此路径添加反向边，同时修改路径上每条边的容量
     v = m;
     while( Prev[v] )
     {
         G[Prev[v]][v] -= nMinFlow;
         G[v][Prev[v]] += nMinFlow;
         v = Prev[v];
     }
     return nMinFlow;
 }
 int main()
 {
     while (cin >> n >> m )
     {
 //m是顶点数目，顶点编号从1开始
         int i,j,k;
         int s,e,c;
         memset( G,,sizeof(G));
         for( i = ; i < n; i ++ )
         {
             cin >> s >> e >> c;
             G[s][e] += c; //两点之间可能有多条边
         }
         unsigned int MaxFlow = ;
         unsigned int aug;
         while( aug = Augment() )
             MaxFlow += aug;
         cout << MaxFlow << endl;
     }
     return ;
 }

题目+代码

　　Dinic 算法

　　Edmonds-Karp的提高余地：需要多次从s到t调用BFS，可以设法减少调用次数。

　　亦即：使用一种代价较小的高效增广方法。

　　考虑：在一次增广的过程中，寻找多条增广路径。

　　DFS

　　先利用 BFS对残余网络分层,分完层后，利用DFS从前一层向后一层反复寻找增广路(即要求DFS的每一步都必须要走到下一层 的节点）。

　　一个节点的“层”数，就是源点到它最少要经过的边数。

　　DFS过程中，要是碰到了汇点，则说明找到了一条增广 路径。此时要增加总流量的值，消减路径上各边的容 量，并添加反向边，即所谓的进行增广。

　　DFS找到一条增广路径后，并不立即结束，而是回溯后 继续DFS寻找下一个增广路径。

　　回溯到的节点u满足以下条件：

　　1) DFS搜索树的树边(u,v)上的容量已经变成0。即刚刚找到的增广路径上所增加的流量，等于(u,v)本次增广前的容量。(DFS的过程中，是从u走到更下层的v的) 　　2)u是满足条件 1)的最上层的节点

　　如果回溯到源点而且无法继续往下走了，DFS结束。

　　因此，一次DFS过程中，可以找到多条增广路径。 DFS结束后，对残余网络再次进行分层，然后再进行DFS

　　当残余网络的分层操作无法算出汇点的层次（即BFS到达不了汇点）时，算法结束，最大流求出。 一般用栈实现DFS,这样就能从栈中提取出增广路径。 Dinic 复杂度是 n*n*m (n是点数，m是边数）

　　要求出最大流中每条边的流量，怎么办？

　　将原图备份，原图上的边的容量减去做完最大 流的残余网络上的边的剩余容量，就是边的流量。

例题：1.POJ 1273 Drainage Ditches

 #include <cstring>
 #include <iostream>
 #include <queue>
 using namespace std;
 #define INFINITE 999999999 //Poj 1273 Drainage Ditches 的 Dinic算法
 int G[][];
 bool Visited[];
 int Layer[];
 int n,m; //1是源点，m是汇点
 bool CountLayer()
 {
     int layer = ;
     deque<int>q;
     memset(Layer,0xff,sizeof(Layer)); //都初始化成-1
     Layer[] = ;
     q.push_back();
     while( ! q.empty())
     {
         int v = q.front();
         q.pop_front();
         for( int j = ; j <= m; j ++ )
         {
             if( G[v][j] >  && Layer[j] == - )
             {
 //Layer[j] == -1 说明j还没有访问过
                 Layer[j] = Layer[v] + ;
                 if( j == m ) //分层到汇点即可
                     return true;
                 else
                     q.push_back(j);
             }
         }
     }
     return false;
 }
 int Dinic()
 {
     int i;
     int s;
     int nMaxFlow = ;
     deque<int> q; //DFS用的栈
     while( CountLayer() )   //只要能分层
     {
         q.push_back(); //源点入栈
         memset(Visited,,sizeof(Visited));
         Visited[] = ;
         while( !q.empty())
         {
             int nd = q.back();
             if( nd == m )   // nd是汇点
             {
 //在栈中找容量最小边
                 int nMinC = INFINITE;
                 int nMinC_vs; //容量最小边的起点
                 for( i = ; i < q.size(); i ++ )
                 {
                     int vs = q[i-];
                     int ve = q[i];
                     if( G[vs][ve] >  )
                     {
                         if( nMinC > G[vs][ve] )
                         {
                             nMinC = G[vs][ve];
                             nMinC_vs = vs;
                         }
                     }
                 }
 //增广，改图
                 nMaxFlow += nMinC;
                 for( i = ; i < q.size(); i ++ )
                 {
                     int vs = q[i-];
                     int ve = q[i];
                     G[vs][ve] -= nMinC; //修改边容量
                     G[ve][vs] += nMinC; //添加反向边
                 }
 //退栈到 nMinC_vs成为栈顶，以便继续dfs
                 while( !q.empty() && q.back() != nMinC_vs )
                 {
                     Visited[q.back()] = ; //没有这个应该也对
                     q.pop_back();
                 }
             }
             else   //nd不是汇点
             {
                 for( i = ; i <= m; i ++ )
                 {
                     if( G[nd][i] >  && Layer[i] == Layer[nd] +  &&
                             ! Visited[i])
                     {
 //只往下一层的没有走过的节点走
                         Visited[i] = ;
                         q.push_back(i);
                         break;
                     }
                 }
                 if( i > m) //找不到下一个点
                     q.pop_back(); //回溯
             }
         }
     }
     return nMaxFlow;
 }
 int main()
 {
     while (cin >> n >> m )
     {
         int i,j,k;
         int s,e,c;
         memset( G,,sizeof(G));
         for( i = ; i < n; i ++ )
         {
             cin >> s >> e >> c;
             G[s][e] += c; //两点之间可能有多条边
         }
         cout << Dinic() << endl;
     }
     return ;
 }

Poj 1273 的 Dinic算法

　　　2.POJ 3436 ACM Computer Factory

题目：
电脑公司生产电脑有N个机器，每个机器单位时间产量为Qi。电脑由P个部件组成，每个机器工作时只能把有某些部件的半成品电脑(或什么都没有的空电脑）变成有另一些部件的半成品电脑或完整电脑(也可能移除某些部件）。求电脑公司的单位时间最大产量，以及哪些机器有协作关系，即一台机器把它的产品交给哪些机器加工。
Sample input

Sample output

输入：电脑由3个部件组成，共有4台机器，1号机器产量15, 能给空电脑加
上2号部件，2号 机器能给空电脑加上2号部件和3号部件, 3号机器能把
有1个2号部件和3号部件有无均可的电脑变成成品（每种部件各有一个）
输出：单位时间最大产量25,有两台机器有协作关系，
1号机器单位时间内要将15个电脑给3号机器加工
2号机器单位时间内要将10个电脑给3号机器加工

建模分析：
每个工厂有三个动作：
)接收原材料
)生产
)将其产出的半成品给其他机器，或产出成品。
这三个过程都对应不同的流量。

网络流模型：
) 添加一个原点S,S提供最初的原料 ...
) 添加一个汇点T, T接受最终的产品 ....
) 将每个机器拆成两个点: 编号为i的接收节点，和编号为i+n的产出节点（n是机器数目），前者用于接收原料，后者用于提供加工后的半成品或成品。这两个点之间要连一条边，容量为单位时间产量Qi
) S 连边到所有接收 "0000..." 或 "若干个0及若干个2"的机器，容量为无穷大
) 产出节点连边到能接受其产品的接收节点，容量无穷大
) 能产出成品的节点，连边到T，容量无穷大。
) 求S到T的最大流

题目+分析

　　  3.poj 2112 Optimal Milking

题目：
有K台挤奶机器和C头牛(统称为物体），每台挤奶机器只能容纳M头牛进行挤奶。现在给出dis[K + C][K + C]的矩阵，dis[i][j]若不为0则表示第i个物体到第j个物体之间有路，dis[i][j]就是该路的长度。（ <= K <= , <=C <= ）
现在问你怎么安排这C头牛到K台机器挤奶，使得需要走最长路程到挤奶机器的奶牛所走的路程最少，求出这个最小值。

Sample Input
   // K C M

Sample Output

分析：
利用Floyd算法求出每个奶牛到每个挤奶机的最短距离。
则题目变为：
已知C头奶牛到K个挤奶机的距离，每个挤奶机只能有M个奶牛，每个奶牛只能去一台挤奶机，求这些奶牛到其要去的挤奶机距离的最大值的最小值。

网络流模型：
每个奶牛最终都只能到达一个挤奶器，每个挤奶器只能有M个奶牛，可把奶牛看做网络流中的流。
每个奶牛和挤奶器都是一个节点，添加一个源，连边到所有奶牛节点，这些边容量都是1。
添加一个汇点，每个挤奶器都连边到它。这些边的容量都是M。

网络流模型：
先假定一个最大距离的的最小值 maxdist, 在上述图中，如果奶牛节点i和挤奶器节点j之间的距离<=maxdist,则从i节点连一条边到j节点，表示奶牛i可以到挤奶器j去挤奶。该边容量为1。该图上的最大流如果是C(奶牛数），那么就说明假设的 maxdist成立，则减小 maxdist再试
总之，要二分 maxdist, 对每个maxdist值，都重新构图，看其最大流是否是C，然后再决定减少或增加maxdist

题目+分析