L1和L2：损失函数和正则化

作为损失函数

L1范数损失函数

　　L1范数损失函数，也被称之为最小绝对值误差。总的来说，它把目标值$Y_i$与估计值$f(x_i)$的绝对差值的总和最小化。

$$S=\sum_{i=1}^n|Y_i-f(x_i)|$$

L2范数损失函数

　　L2范数损失函数，也被称为最小平方误差，总的来说，它把目标值$Y_i$与估计值$f(x_i)$的差值的平方和最小化。

$$S=\sum_{i=1}^n(Y_i-f(x_i))^2$$

L1损失函数	L2损失函数
鲁棒	不是很鲁棒
不稳定性	稳定解
可能多个解	总是一个解

　　总结一下：L2范数loss将误差平均化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大，因此模型会对样本更加敏感，这就需要调整模型来最小化误差。如果有个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其他正常的样本，因为这些正常的样本的误差比这单个的异常值的误差小。

作为正则化

　　我们经常会看见损失函数后面添加一个额外项，一般为L1-norm,L2-norm，中文称作L1正则化和L2正则化，或者L1范数和L2函数。

　　L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。防止模型过拟合而加在损失函数后面的一项。

L1正规化

　　L1范数符合拉普拉斯分布，是不完全可微的。表现在图像上会有很多角出现。这些角和目标函数的接触机会远大于其他部分。就会造成最优值出现在坐标轴上，因此就会导致某一维的权重为0 ，产生稀疏权重矩阵，进而防止过拟合。

最小平方损失函数的L1正则化：

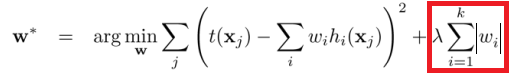
L1正则化是指权值向量$w$中各个元素的绝对值之和

L2正规化

　　L2范数符合高斯分布，是完全可微的。和L1相比，图像上的棱角被圆滑了很多。一般最优值不会在坐标轴上出现。在最小化正则项时，可以是参数不断趋向于0，最后活的很小的参数。

  在机器学习中，正规化是防止过拟合的一种重要技巧。从数学上讲，它会增加一个正则项，防止系数拟合得过好以至于过拟合。L1与L2的区别只在于，L2是权重的平方和，而L1就是权重的和。如下：

最小平方损失函数的L2正则化：

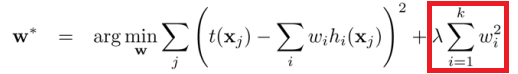
L2正则化是指权值向量$w$中各个元素的平方和然后再求平方根

作用

L1正则化

• 优点：输出具有稀疏性，即产生一个稀疏模型，进而可以用于特征选择；一定程度上，L1也可以防止过拟合
• 缺点：但在非稀疏情况下计算效率低

L2正则化：

• 优点：计算效率高（因为存在解析解）；可以防止模型过拟合（overfitting）
• 缺点：非稀疏输出；无特征选择

稀疏模型和特征选择：稀疏性我在这篇文章有详细讲解，如果特征符合稀疏性，说明特征矩阵很多元素为0，只有少数元素是非零的矩阵，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，或者贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。

文献[1]解释了为什么L1正则化可以产生稀疏模型（L1是怎么样系数等于0的），以及为什么L2正则化可以防止过拟合，由于涉及到很多公式，想要详细了解的同学，请移步。

区别

1、L1正则化是模型各个参数的绝对值之和。

　 L2正则化是模型各个参数的平方和的开方值。

2、L1会趋向于产生少量的特征，而其他的特征都是0，产生稀疏权重矩阵。

　 L2会选择更多的特征，这些特征都会接近于0。

再讨论几个问题

1.为什么参数越小代表模型越简单？

　　越是复杂的模型，越是尝试对所有样本进行拟合，包括异常点。这就会造成在较小的区间中产生较大的波动，这个较大的波动也会反映在这个区间的导数比较大。

　　只有越大的参数才可能产生较大的导数。因此参数越小，模型就越简单。

2.实现参数的稀疏有什么好处？

　　因为参数的稀疏，在一定程度上实现了特征的选择。一般而言，大部分特征对模型是没有贡献的。这些没有用的特征虽然可以减少训练集上的误差，但是对测试集的样本，反而会产生干扰。稀疏参数的引入，可以将那些无用的特征的权重置为0.

3.L1范数和L2范数为什么可以避免过拟合？

　　加入正则化项就是在原来目标函数的基础上加入了约束。当目标函数的等高线和L1，L2范数函数第一次相交时，得到最优解。

参考文献

CSDN博客：机器学习中正则化项L1和L2的直观理解

Differences between L1 and L2 as Loss Function and Regularization