机器学习——Bagging与随机森林算法及其变种

Bagging算法： 

　　凡解：给定M个数据集，有放回的随机抽取M个数据，假设如此抽取3组，3组数据一定是有重复的，所以先去重。去重后得到3组数据，每组数据量分别是s1,s2,s3，然后三组分别训练组合成一个强模型。如下图：

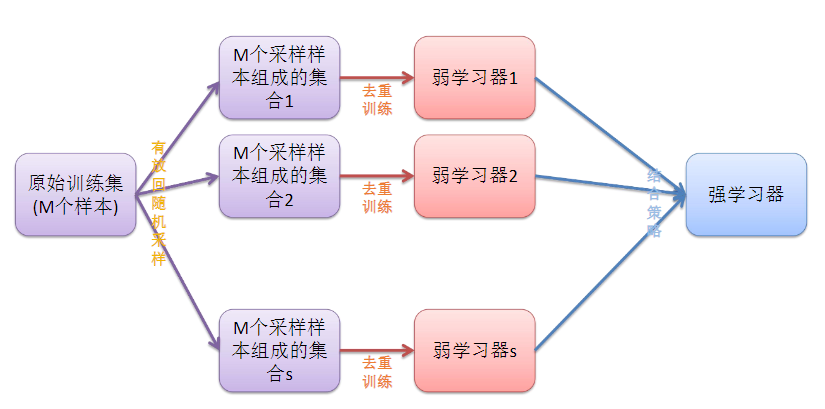
随机森林算法：

　　一般用于大规模数据，百万级以上的。

　　在Bagging算法的基础上，如上面的解释，在去重后得到三组数据，那么再随机抽取三个特征属性，选择最佳分割属性作为节点来创建决策树。可以说是

随机森林=决策树+Bagging

 如下图

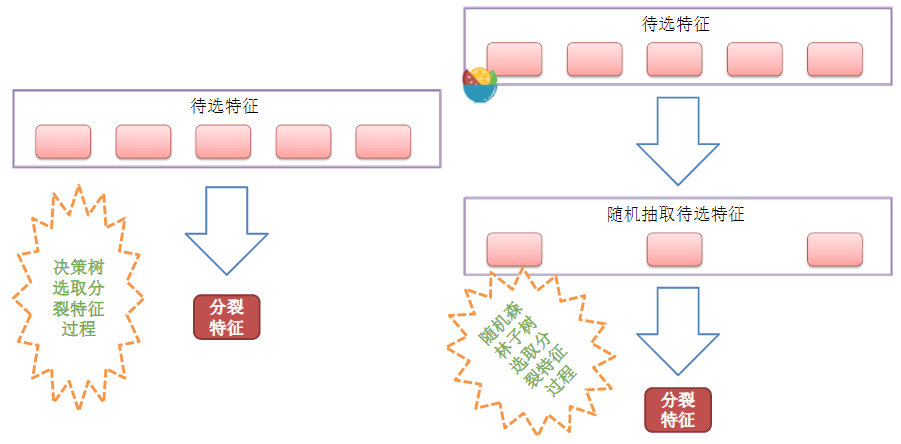
RF(随机森林）的变种：

　　ExtraTree算法

　　凡解：和随机森林的原理基本一样。主要差别点如下

①随机森林是在含有m个数据的原数据集上有放回的抽取m个数据，而ExtraTree算法是直接用原数据集训练。

②随机森林在选择划分特征点的时候会和传统决策树一样，会基于信息增益、信息增益率、基尼系数、均方差等原则来选择最优特征值；而ExtraTree会随机的选择一个特征值来划分决策树。

　　TRTE算法

　　不重要，了解一下即可

　　官解：TRTE是一种非监督的数据转化方式。对特征属性重新编码，将低维的数据集映射到高维，从而让映射到高维的数据更好的应用于分类回归模型。

　　划分标准为方差

　　看例子吧直接：

　　

　　IForest

　　IForest是一种异常点检测算法，使用类似RF的方式来检测异常点

　　此算法比较坑，适应性不强。

　　1.在随机采样的过程中，一般只需要少量数据即可；

　　•2.在进行决策树构建过程中，IForest算法会随机选择一个划分特征，并对划分特征随机选择一个划分阈值；

　　•3.IForest算法构建的决策树一般深度max_depth是比较小的。

　　此算法可以用，但此算法连创作者本人也无法完整的解释原理。

RF（随机森林）的主要优点:

●1.训练可以并行化，对于大规模样本的训练具有速度的优势;

●2.由于进行随机选择决策树划分特征列表，这样在样本维度比较高的时候，仍然具有比较高的训练性能;

●3.可以给出各个特征的重要性列表;
●4.由于存在随机抽样,训练出来的模型方差小，泛化能力强;
●5. RF实现简单;
●6.对于部分特征的缺失不敏感。
RF的主要缺点:
●1.在某些噪音比较大的特征上(数据特别异常情况)，RF模型容易陷入过拟合;
●2.取值比较多的划分特征对RF的决策会产生更大的影响，从而有可能影响模型的
效果。

随机树主要参数，划线部分为主要调整的参数