UVa 1151 买还是建

https://vjudge.net/problem/UVA-1151

题意：

平面上有n个点，你的任务是让所有n个点连通。为此，你可以新建一些边，费用等于两个端点的距离平方和。另外还有q个套餐可以购买，如果你购买了第i个套餐，该套餐中的所有结点都变得相互连通，第i个套餐的花费为Ci。

思路:

这道题比较容易超时。可能需要用到并查集的路径压缩，我下面的代码就是用了路径压缩，不然要超时。也是看了别人的代码才知道还有这种省时间的做法。

先介绍一下路径压缩吧：

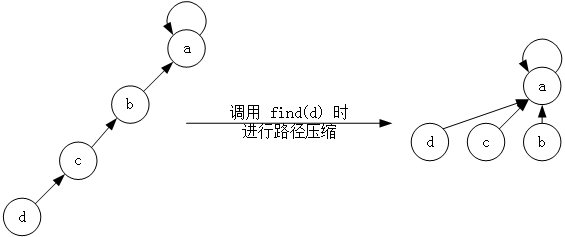
如果并查集像一字长蛇这样排列的话，寻找起来就比较费时间，但如果像图2一样的话，一下子就可以找到根了。压缩的方法也是挺简单的。

     int r = x;
     while (r != p[r])  r = p[r];
     int i = x, j;
     while (p[i] != r)
     {
         j = p[i];
         p[i] = r;
         i = j;
     }

题目的做法就像紫书上说的那样，先不考虑套餐算一遍，然后枚举套餐的方法，这里的话二进制枚举法非常方便。

 #include<iostream>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 using namespace std;
 
 const int maxn =  + ;
 
 int n, m, q, cnt;
 int p[maxn];
 vector<int> g[];  //方案集合
 int c[];          //方案价格
 
 //边
 struct node
 {
     int u;
     int v;
     int dist;
 }edge[maxn*maxn];
 
 //点
 struct node2
 {
     int x, y;
 }a[maxn];
 
 int find(int x)
 {
     //return p[x] == x ? x : find(p[x]);   用这个会超时
     //路径压缩
     int r = x;
     while (r != p[r])  r = p[r];
     int i = x, j;
     while (p[i] != r)
     {
         j = p[i];
         p[i] = r;
         i = j;
     }
     return r;
 }
 
 bool cmp(node a, node b)
 {
     return a.dist < b.dist;
 }
 
 //计算距离平方和
 int cacl_dist(node2 a, node2 b)
 {
     return (a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y);
 }
 
 void init()
 {
     for (int k = ; k <= n; k++)   p[k] = k;
 }
 
 int Kruskal()
 {
     int num = ;
     int ans = ;
     for (int i = ; i < cnt ; i++)
     {
         int x = find(edge[i].u);
         int y = find(edge[i].v);
         if (x != y)
         {
             p[x] = y;
             ans += edge[i].dist;
             num++;
         }
         if (num == n - )  return ans;
     }
     return ans;
 }
 
 void solve()
 {
     init();
     int ans = Kruskal();
     //二进制枚举方案
     for (int i = ; i < ( << q); i++)
     {
         init();
         int cost = ;
         for (int j = ; j < q; j++)
         {
             if (i & ( << j))
             {
                 cost += c[j];
                 int x = find(g[j][]);
                 for (int k = ; k < g[j].size(); k++)
                 {
                     int y = find(g[j][k]);
                     if (x != y)
                         p[y] = x;
                 }
             }
         }
         ans = min(cost + Kruskal(), ans);
     }
     printf("%d\n", ans);
 }
 
 int main()
 {
     //freopen("D:\\txt.txt", "r", stdin);
     int T, t, s, kase=;
     scanf("%d", &T);
     while (T--)
     {
         if (++kase > )    printf("\n");
         scanf("%d%d", &n, &q);
 
         //存储方案
         for (int i = ; i < q; i++)
         {
             g[i].clear();
             scanf("%d", &t);
             scanf("%d", &c[i]);
             for (int j = ; j < t; j++)
             {
                 scanf("%d", &s);
                 g[i].push_back(s);
             }
         }
 
         for (int i = ; i <= n; i++)
             scanf("%d%d", &a[i].x, &a[i].y);
 
         //存储边
         cnt = ;
         for (int i = ; i <= n;i++)
         for (int j = i + ; j <= n; j++)
         {
             edge[cnt].u = i;
             edge[cnt].v = j;
             edge[cnt].dist = cacl_dist(a[i], a[j]);
             cnt++;
         }
         sort(edge, edge + cnt, cmp);
         solve();
     }
     return ;
 }