2017 icpc 沈阳网络赛
cable cable cable
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 278 Accepted Submission(s): 224
Now you have M
display screens and K
different signal sources(K≤M≤232
−1
). Select K
display screens from M
display screens, how many cables are needed at least so that **any** K
display screens you select can show exactly K
different colors.
), for each test case:
there is one line contains two integers M
and K
.
.
20 15
90
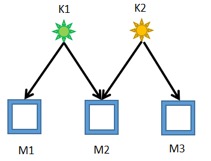
As the picture is shown, when you select M1 and M2, M1 show the color of K1, and M2 show the color of K2.
When you select M3 and M2, M2 show the color of K1 and M3 show the color of K2.
When you select M1 and M3, M1 show the color of K1.
#include<bits/stdc++.h>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long
#define mod 998244353
using namespace std;
const int N=1e5+;
LL n,m,k;
int main()
{
while(scanf("%lld%lld",&n,&k)!=EOF)
{
printf("%lld\n",k*(n-k+));
}
return ;
}
array array array
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 444 Accepted Submission(s): 275
Kiddo: "I have an array A
and a number k
, if you can choose exactly k
elements from A
and erase them, then the remaining array is in non-increasing order or non-decreasing order, we say A
is a magic array. Now I want you to tell me whether A
is a magic array. " Conan: "emmmmm..." Now, Conan seems to be in trouble, can you help him?
and k
in one line, then one line with n
integers: A1
,A
2
…A
n
.
1≤T≤20
1≤n≤105
0≤k≤n
1≤Ai
≤10
5
4 1
1 4 3 7
5 2
4 1 3 1 2
6 1
1 4 3 5 4 6
A is a magic array.
A is not a magic array.
#include<bits/stdc++.h>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long
#define mod 998244353
using namespace std;
const int N=1e5+;
int n,m,k,t;
int a[N],bit[N],maxn;
int maxed(int i)
{
int s=;
while(i>)
{
s=max(bit[i],s);
i-=i&-i;
}
return s;
}
void add(int i,int x)
{
while(i<N)
{
bit[i]=max(bit[i],x);
i+=i&-i;
}
return ; }
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&k);
for(int i=;i<=n;i++)
{
scanf("%d",&a[i]);
}
clr(bit);
maxn=;
for(int i=;i<=n;i++)
{
t=maxed(a[i])+;
if(t>maxn)
maxn=t;
add(a[i],t);
}
clr(bit);
for(int i=n;i>=;i--)
{
t=maxed(a[i])+;
if(t>maxn)
maxn=t;
add(a[i],t);
}
if(n-k<=maxn)
printf("A is a magic array.\n");
else
printf("A is not a magic array.\n");
}
return ;
}
number number number
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 390 Accepted Submission(s): 247
:
⋅
F0
=0,F
1
=1
;
⋅
Fn
=F
n−1
+F
n−2
(n≥2)
.
Give you an integer k
, if a positive number n
can be expressed by
n=Fa
1
+F
a
2
+...+F
a
k
where 0≤a1
≤a
2
≤⋯≤a
k
, this positive number is mjf−good
. Otherwise, this positive number is mjf−bad
.
Now, give you an integer k
, you task is to find the minimal positive mjf−bad
number.
The answer may be too large. Please print the answer modulo 998244353.
Each test case includes an integer k
which is described above. (1≤k≤109
)
number mod 998244353.
#include<bits/stdc++.h>
#define clr(x) memset(x,0,sizeof(x))
#define LL long long
#define mod 998244353
using namespace std;
typedef vector<LL> vec;
typedef vector<vec> mat;
mat ori(,vec()),orip(,vec());
mat mart(,vec()),martp(,vec());
mat mul(const mat &a,const mat &b)
{
int row=a.size();
int col=b[].size();
int mid=b.size();
mat c(row,vec(col));
for(int i=;i<row;i++)
for(int j=;j<col;j++)
for(int k=;k<mid;k++)
c[i][j]=(c[i][j]+a[i][k]*b[k][j]%mod)%mod;
return c;
}
mat quick_pow(mat a,LL n)
{
int len=a.size();
mat res(len,vec(len));
for(int i=;i<len;i++)
res[i][i]=;
while(n)
{
if(n&)
res=mul(res,a);
a=mul(a,a);
n>>=;
}
return res;
}
void init()
{
orip[][]=;
orip[][]=;
orip[][]=;
martp[][]=;
martp[][]=;
martp[][]=;
martp[][]=;
martp[][]=;
martp[][]=;
return ;
}
int main()
{
LL n,m;
init();
while(scanf("%lld",&n)!=EOF)
{
ori=orip;
mart=martp;
mart=quick_pow(mart,n-);
ori=mul(ori,mart);
printf("%lld\n",ori[][]);
}
return ;
}
transaction transaction transaction
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 132768/132768 K (Java/Others)
Total Submission(s): 877 Accepted Submission(s): 431
As we know, the price of this book was different in each city. It is a
yuan
in i
t
city. Kelukin will take taxi, whose price is 1
yuan
per km and this fare cannot be ignored.
There are n−1
roads connecting n
cities. Kelukin can choose any city to start his travel. He want to know the maximum money he can get.
(1≤T≤10
) , the number of test cases.
For each test case:
first line contains an integer n
(2≤n≤100000
) means the number of cities;
second line contains n
numbers, the i
th
number means the prices in i
th
city; (1≤Price≤10000)
then follows n−1
lines, each contains three numbers x
, y
and z
which means there exists a road between x
and y
, the distance is z
km
(1≤z≤1000)
.
4
10 40 15 30
1 2 30
1 3 2
3 4 10
#include<bits/stdc++.h>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define LL long long
#define mod 998244353
using namespace std;
const int N=1e5+;
int T;
int n,m,u,v;
LL a[N],ck,maxn,ans,leftmin[N],allmin[N];
struct edg
{
int next,to;
LL val;
}edge[N*];
int head[N],ecnt,cnt;
void addedge(int u,int v,LL val)
{
edge[++ecnt]=(edg){head[u],v,val};
head[u]=ecnt;
return ;
}
void dfs(int u,int pre,LL val)
{
leftmin[u]=a[u];
for(int i=head[u];i!=-;i=edge[i].next)
{
if(edge[i].to!=pre)
{
dfs(edge[i].to,u,edge[i].val);
leftmin[u]=min(leftmin[edge[i].to]+edge[i].val,leftmin[u]);
}
}
return ;
}
void dfs2(int u,int pre,LL val)
{
allmin[u]=min(allmin[pre]+val,leftmin[u]);
maxn=max(maxn,a[u]-allmin[u]);
for(int i=head[u];i!=-;i=edge[i].next)
{
if(edge[i].to!=pre)
{
dfs2(edge[i].to,u,edge[i].val);
}
}
return ;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
clr_1(head);
ecnt=cnt=;
ans=maxn=;
for(int i=;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=;i<n;i++)
{
scanf("%d%d%lld",&u,&v,&ck);
addedge(u,v,ck);
addedge(v,u,ck);
}
allmin[]=0x3f3f3f3f;
dfs(,,);
dfs2(,,);
printf("%lld\n",maxn);
}
return ;
}
card card card
Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1100 Accepted Submission(s): 487
One day, MJF takes a stack of cards and talks to him: let's play a game and if you win, you can get all these cards. MJF randomly assigns these cards into n
heaps, arranges in a row, and sets a value on each heap, which is called "penalty value".
Before the game starts, WYJ can move the foremost heap to the end any times.
After that, WYJ takes the heap of cards one by one, each time he needs to move all cards of the current heap to his hands and face them up, then he turns over some cards and the number of cards he turned is equal to the penaltyvalue
.
If at one moment, the number of cards he holds which are face-up is less than the penaltyvalue
, then the game ends. And WYJ can get all the cards in his hands (both face-up and face-down).
Your task is to help WYJ maximize the number of cards he can get in the end.So he needs to decide how many heaps that he should move to the end before the game starts. Can you help him find the answer?
MJF also guarantees that the sum of all "penalty value" is exactly equal to the number of all cards.
test cases ending up with EOF.
For each test case:
the first line is an integer n
(1≤n≤106
), denoting n
heaps of cards;
next line contains n
integers, the i
th
integer ai
(0≤ai≤1000
) denoting there are ai
cards in i
th
heap;
then the third line also contains n
integers, the i
th
integer bi
(1≤bi≤1000
) denoting the "penalty value" of i
th
heap is bi
.
4 6 2 8 4
1 5 7 9 2
[pre]
For the sample input:
+ If WYJ doesn't move the cards pile, when the game starts the state of cards is:
4 6 2 8 4
1 5 7 9 2
WYJ can take the first three piles of cards, and during the process, the number of face-up cards is 4-1+6-5+2-7. Then he can't pay the the "penalty value" of the third pile, the game ends. WYJ will get 12 cards.
+ If WYJ move the first four piles of cards to the end, when the game starts the state of cards is:
4 4 6 2 8
2 1 5 7 9
WYJ can take all the five piles of cards, and during the process, the number of face-up cards is 4-2+4-1+6-5+2-7+8-9. Then he takes all cards, the game ends. WYJ will get 24 cards.
It can be improved that the answer is 4.
**huge input, please use fastIO.**
[/pre]
#include<bits/stdc++.h>
#define clr(x) memset(x,0,sizeof(x))
#define clr_1(x) memset(x,-1,sizeof(x))
#define mod 1000000007
using namespace std;
const int N=1e6+;
typedef long long LL;
inline void getInt(LL* p) {
char ch;
do {
ch = getchar();
} while (ch == ' ' || ch == '\n');
if (ch == '-') {
*p = -(getchar() - '');
while ((ch = getchar()) >= '' && ch <= '') {
*p = *p * - ch + '';
}
}
else {
*p = ch - '';
while ((ch = getchar()) >= '' && ch <= '') {
*p = *p * + ch - '';
}
}
}
LL a[N],b[N],ans,maxn,lz,num;
int n,m,T,pos,prepos,rpos;
int main()
{
while(scanf("%d",&n)!=EOF)
{
for(int i=;i<=n;i++)
{
getInt(&a[i]);
}
for(int i=;i<=n;i++)
{
getInt(&b[i]);
}
maxn=;
ans=;
num=;
prepos=;
pos=;
rpos=;
for(int i=;i<=n;i++)
{
ans+=a[i]-b[i];
num+=a[i];
if(ans<)
{
prepos=pos;
pos=i;
if(num>maxn)
{
rpos=prepos;
maxn=num;
}
ans=;
num=;
}
}
for(int i=;i<=n;i++)
{
ans+=a[i]-b[i];
num+=a[i];
if(ans<)
{
prepos=pos;
pos=i;
if(num>maxn)
{
rpos=prepos;
maxn=num;
}
ans=;
num=;
if(prepos<=pos) break;
}
if(pos==i)
{
rpos=pos;
break;
}
}
printf("%d\n",rpos);
}
return ;
}
string string string
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1452 Accepted Submission(s): 416
Given a string s, we define a substring that happens exactly k times as an important string, and you need to find out how many substrings which are important strings.
For each test case, there are two lines:
the first line contains an integer k (k≥1) which is described above;
the second line contain a string s (length(s)≤105).
It's guaranteed that ∑length(s)≤2∗106.
2
abcabc
3
abcabcabcabc
9
这题是不同长度串和长度为k的串的总数的综合体。k=1统计的是该字符串不同的子串的个数，k>1统计的是该字符串出现恰好k次的子串个数。k=1论文题，无需赘言。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#define clr(x) memset(x,0,sizeof(x))
#define clrmax(x) memset)x,0x3f3f3f3f,sizeof(x))
using namespace std;
const int N=1e5+;
int ranked[N],order[N],backet[N],sa[N],key1[N],key2[N],height[N];
char s[N],vis[];
int n,m,ans,k;
int unrep[N];
multiset<int> sum;
multiset<int>::iterator it;
bool cmp(int *r,int a,int b,int len)
{
return r[a]==r[b] && r[a+len]==r[b+len];
}
void da(int *sa,char *r,int n,int m)
{
int i,j,p,*x=key1,*y=key2,*t;
for(i=;i<m;i++) backet[i]=;
for(i=;i<n;i++) backet[x[i]=r[i]]++;
for(i=;i<m;i++) backet[i]+=backet[i-];
for(i=n-;i>=;i--) sa[--backet[x[i]]]=i;
for(j=,p=;p<n;j*=,m=p)
{
for(p=,i=n-j;i<n;i++) y[p++]=i;
for(i=;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=;i<n;i++) order[i]=x[y[i]];
for(i=;i<m;i++) backet[i]=;
for(i=;i<n;i++) backet[order[i]]++;
for(i=;i<m;i++) backet[i]+=backet[i-];
for(i=n-;i>=;i--) sa[--backet[order[i]]]=y[i];
for(t=x,x=y,y=t,p=,x[sa[]]=,i=;i<n;i++)
x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;
}
return ;
}
void calheight(int *sa,char *r,int n)
{
int i,j,k=;
for(i=;i<=n;i++) ranked[sa[i]]=i;
for(i=;i<n;i++)
{
if(k) k--;
j=sa[ranked[i]-];
while(r[i+k]==r[j+k]) k++;
height[ranked[i]]=k;
}
return ;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
ans=;
scanf("%d",&k);
scanf("%s",s);
n=strlen(s);
n++;
da(sa,s,n,);
n--;
calheight(sa,s,n);
if(k==)
{
height[]=height[n+]=;
for(int i=;i<=n;i++)
ans+=n-sa[i]-max(height[i],height[i+]);
printf("%d\n",ans);
continue;
}
sum.clear();
k--;
height[]=;
height[n+]=;
for(int i=;i<=k;i++)
sum.insert(height[i]);
for(int i=k+;i<=n;i++)
{
sum.insert(height[i]);
it=sum.begin();
ans+=max(*it-max(height[i-k],height[i+]),);
sum.erase(sum.find(height[i-k+]));
}
printf("%d\n",ans);
}
return ;
}
2017 icpc 沈阳网络赛的更多相关文章
- 2018 ICPC 沈阳网络赛
2018 ICPC 沈阳网络赛 Call of Accepted 题目描述:求一个算式的最大值与最小值. solution 按普通算式计算方法做,只不过要同时记住最大值和最小值而已. Convex H ...
- 2017 icpc 南宁网络赛
2000年台湾大专题...英语阅读输入输出专场..我只能说很强势.. M. Frequent Subsets Problem The frequent subset problem is define ...
- 2017 icpc 西安网络赛
F. Trig Function 样例输入 2 0 2 1 2 2 样例输出 998244352 0 2 找啊找啊找数列和论文.cosnx可以用切比雪夫多项式弄成(cosx)的多项式,然后去找到了相关 ...
- 2018 ICPC 沈阳网络赛预赛 Supreme Number（找规律）
[传送门]https://nanti.jisuanke.com/t/31452 [题目大意]:给定一个数字(最大可达10100),现在要求不超过它的最大超级质数.超级质数定义:对于一个数,把它看成数字 ...
- 2019 ICPC 沈阳网络赛 J. Ghh Matin
Problem Similar to the strange ability of Martin (the hero of Martin Martin), Ghh will random occurr ...
- 2018 ICPC 徐州网络赛
2018 ICPC 徐州网络赛 A. Hard to prepare 题目描述:\(n\)个数围成一个环,每个数是\(0\)~\(2^k-1\),相邻两个数的同或值不为零,问方案数. solution ...
- hdu6212[区间dp] 2017青岛ACM-ICPC网络赛
原题: BZOJ1032 (原题数据有问题) /*hdu6212[区间dp] 2017青岛ACM-ICPC网络赛*/ #include <bits/stdc++.h> using name ...
- 2019 ICPC 南昌网络赛
2019 ICPC 南昌网络赛 比赛时间:2019.9.8 比赛链接:The 2019 Asia Nanchang First Round Online Programming Contest 总结 ...
- 沈阳网络赛 F - 上下界网络流
"Oh, There is a bipartite graph.""Make it Fantastic." X wants to check whether a ...
随机推荐
- Mac 上真机调试cocos2d-x-3.16的test程序
文章比较长,一个算是新手又不是新手的程序员的解决过程. 一 xcode中打开项目 首先,下载完成cocos2d-x-3.16之后,解压,然后在根目录build目录下双击cocos2d_tests.xc ...
- A Simple Math Problem（矩阵快速幂）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1757 思路:矩阵快速幂模板题,不过因为刚刚入门矩阵快速幂,所以经常把数组f存反,导致本地错误一晚,差点 ...
- js中的apply、call、bind
每个函数都包含两个非继承而来的方法,call()和apply(),可以改变函数内部this的指向 1.apply 用另一个对象替换当前对象,接收两个参数,第一个参数表示需要绑定的this变量,第二个参 ...
- Fiddler-- 安装HTTPs证书
1. 现在很多带有比较重要信息的接口都使用了安全性更高的HTTPS,而Fiddler默认是抓取HTTP类型的接口,要想查看HTTPS类型接口就需要安装fiddler证书. 2.打开Fiddler, ...
- 金融分析二：Matplotlib模板
Matplotlib:绘图和可视化 Matplotlib是一个强大的Python绘图和数据可视化的工具包. 安装方法:pip install matplotlib 引用方法:import matplo ...
- devinet_ioctl
Kernel: 4.12.6 deinet_ioctl:获取或者设置接口的地址,掩码,标记等信息: 注意,使用SIOCSIFFLAGS关闭设备,如果使用了别名,则删除对应ip,如果其为主ip,并且从i ...
- ARM linux的启动部分源代码简略分析【转】
转自:http://www.cnblogs.com/armlinux/archive/2011/11/07/2396784.html ARM linux的启动部分源代码简略分析 以友善之臂的mini2 ...
- 64_l6
lightdm-qt5-devel-1.22.0-1.fc26.i686.rpm 19-May-2017 11:11 22854 lightdm-qt5-devel-1.22.0-1.fc26.x86 ...
- oracle to_char 返回毫秒级
select to_char(systimestamp,'yyyy-mm-dd hh24:mi:ssxff') time1, 关键在 systimestamp
- System.getProperty方法中输出路径的方法
package codegenerator;/** *@author Eilen *@date 2017年9月27日---下午3:15:09 *@描述: *@answer */public class ...