codeforces 711E E. ZS and The Birthday Paradox(数学+概率)

题目链接：

E. ZS and The Birthday Paradox、

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

ZS the Coder has recently found an interesting concept called the Birthday Paradox. It states that given a random set of 23 people, there is around 50% chance that some two of them share the same birthday. ZS the Coder finds this very interesting, and decides to test this with the inhabitants of Udayland.

In Udayland, there are 2n days in a year. ZS the Coder wants to interview k people from Udayland, each of them has birthday in one of2n days (each day with equal probability). He is interested in the probability of at least two of them have the birthday at the same day.

ZS the Coder knows that the answer can be written as an irreducible fraction 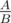. He wants to find the values of A and B (he does not like to deal with floating point numbers). Can you help him?

Input

The first and only line of the input contains two integers n and k (1 ≤ n ≤ 1018, 2 ≤ k ≤ 1018), meaning that there are 2n days in a year and that ZS the Coder wants to interview exactly k people.

Output

If the probability of at least two k people having the same birthday in 2n days long year equals 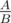 (A ≥ 0, B ≥ 1, 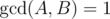), print the A and B in a single line.

Since these numbers may be too large, print them modulo 106 + 3. Note that A and B must be coprime before their remainders modulo106 + 3 are taken.

Examples

input

3 2

output

1 8

input

1 3

output

1 1

input

4 3

output

23 128

题意：

一年有2^n天,现在有k个熊孩子,问至少有两个熊孩子的生日是同一天的概率是多少;

思路：

1-2^n*(2^n-1)*...*(2^n-k+1)/(2^n)^k,然后就是求gcd了,约分后再求逆元,反正这个题涉及的知识点有概率论与组合数学,抽屉原理,勒让德定理,求逆元,快速幂这些,反正我是看别人代码才会的,我好菜啊;

AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <bits/stdc++.h>
#include <stack>
#include <map>

using namespace std;

#define For(i,j,n) for(int i=j;i<=n;i++)
#define mst(ss,b) memset(ss,b,sizeof(ss));

typedef  long long LL;

template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('\n');
}

const LL mod=1e6+3;
const double PI=acos(-1.0);
const int inf=1e9;
const int N=2e5+10;
const int maxn=1e3+520;
const double eps=1e-12;

LL n,k;

int check()
{
    LL s=1;
    for(int i=1;i<=n;i++)
    {
        s=s*2;
        if(s>=k)return 0;
    }
    return 1;
}
LL pow_mod(LL x,LL y)
{
    LL s=1,base=x;
    while(y)
    {
        if(y&1)s=s*base%mod;
        base=base*base%mod;
        y>>=1;
    }
    return s;
}
int main()
{
    read(n);read(k);
    if(check()){cout<<"1 1\n";return 0;}
    LL num=0;
    for(LL i=k-1;i>0;i/=2)num+=i/2;
    LL temp=pow_mod(2,n),ans=1;
    for(LL i=1;i<k;i++)
    {
        ans=ans*(temp-i)%mod;
        if(temp-i==0)break;
    }
    LL ha=pow_mod(2,num);
    ans=ans*pow_mod(ha,mod-2)%mod;
    temp=pow_mod(temp,k-1)*pow_mod(ha,mod-2)%mod;
    cout<<(temp-ans+mod)%mod<<" "<<temp<<endl;

    return 0;
}