<转载> OpenGL Projection Matrix
原文
OpenGL Projection Matrix
Related Topics: OpenGL Transformation
Updates: The MathML version is available here.
Overview
A computer monitor is a 2D surface. A 3D scene rendered by OpenGL must be projected onto the computer screen as a 2D image. GL_PROJECTION matrix is used for this projection transformation. First, it transforms all vertex data from the eye coordinates to the clip coordinates. Then, these clip coordinates are also transformed to the normalized device coordinates (NDC) by dividing with w component of the clip coordinates.
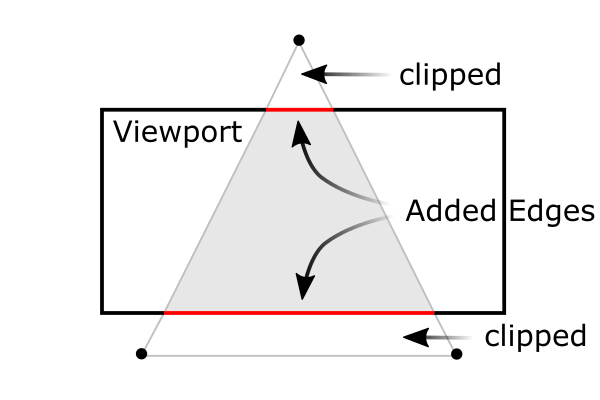
A triangle clipped by frustum
Therefore, we have to keep in mind that both clipping (frustum culling) and NDC transformations are integrated into GL_PROJECTIONmatrix. The following sections describe how to build the projection matrix from 6 parameters; left, right, bottom, top, near and farboundary values.
Note that the frustum culling (clipping) is performed in the clip coordinates, just before dividing by wc. The clip coordinates, xc, ycand zc are tested by comparing with wc. If any clip coordinate is less than -wc, or greater than wc, then the vertex will be discarded. 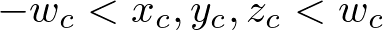
Then, OpenGL will reconstruct the edges of the polygon where clipping occurs.
Perspective Projection
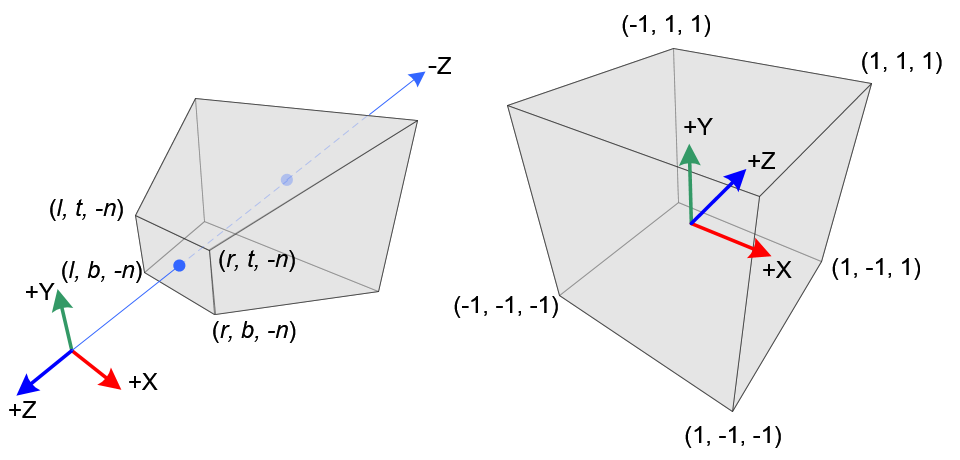
Perspective Frustum and Normalized Device Coordinates (NDC)
In perspective projection, a 3D point in a truncated pyramid frustum (eye coordinates) is mapped to a cube (NDC); the range of x-coordinate from [l, r] to [-1, 1], the y-coordinate from [b, t] to [-1, 1] and the z-coordinate from [n, f] to [-1, 1].
Note that the eye coordinates are defined in the right-handed coordinate system, but NDC uses the left-handed coordinate system. That is, the camera at the origin is looking along -Z axis in eye space, but it is looking along +Z axis in NDC. Since glFrustum() accepts only positive values of near and far distances, we need to negate them during the construction of GL_PROJECTION matrix.
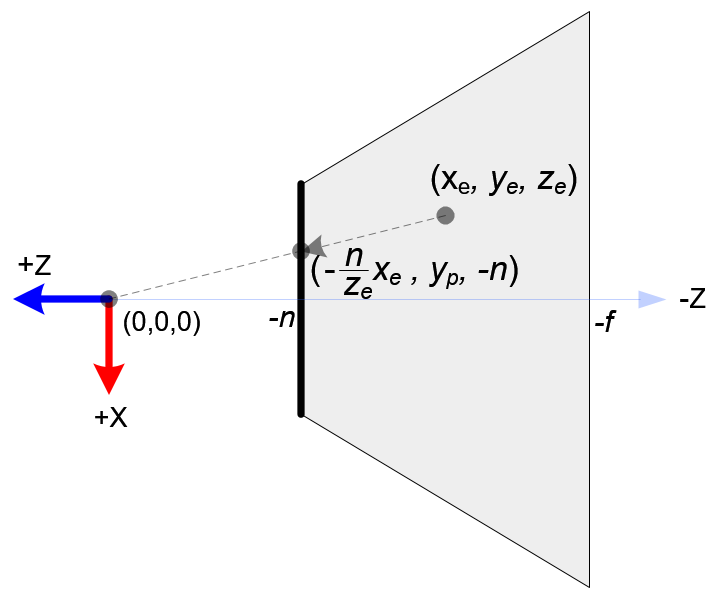
In OpenGL, a 3D point in eye space is projected onto the near plane (projection plane). The following diagrams show how a point (xe, ye, ze) in eye space is projected to (xp, yp, zp) on the near plane.
Top View of Frustum
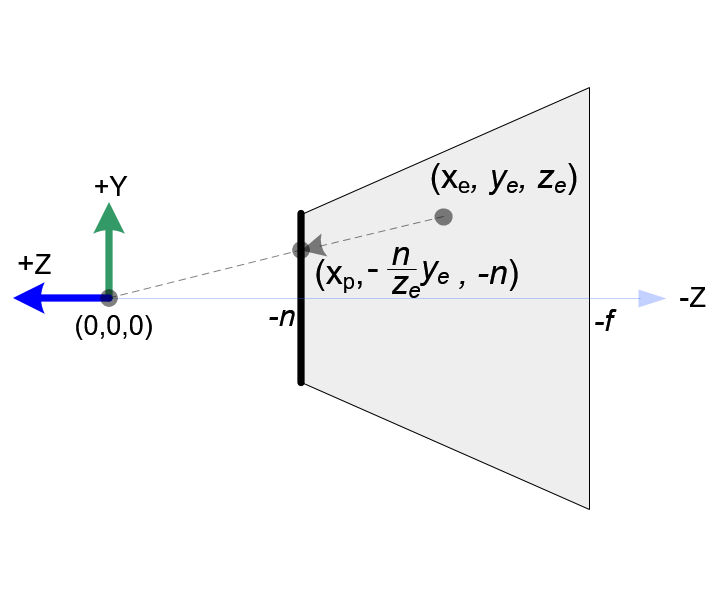
Side View of Frustum
From the top view of the frustum, the x-coordinate of eye space, xe is mapped to xp, which is calculated by using the ratio of similar triangles; 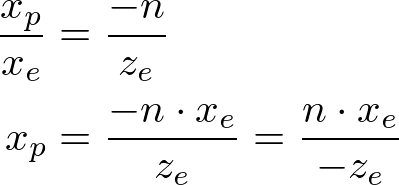
From the side view of the frustum, yp is also calculated in a similar way; 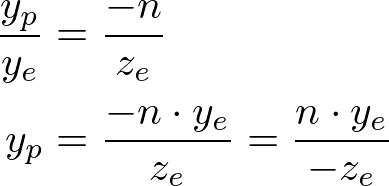
Note that both xp and yp depend on ze; they are inversely propotional to -ze. In other words, they are both divided by -ze. It is a very first clue to construct GL_PROJECTION matrix. After the eye coordinates are transformed by multiplying GL_PROJECTION matrix, the clip coordinates are still a homogeneous coordinates. It finally becomes the normalized device coordinates (NDC) by divided by the w-component of the clip coordinates. (See more details on OpenGL Transformation.)  ,
, 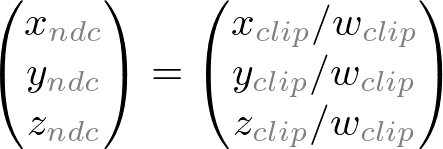
Therefore, we can set the w-component of the clip coordinates as -ze. And, the 4th of GL_PROJECTION matrix becomes (0, 0, -1, 0). 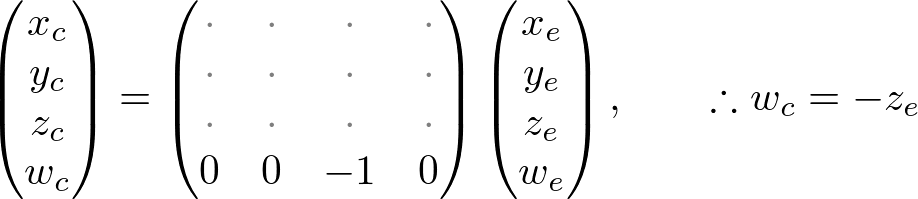
Next, we map xp and yp to xn and yn of NDC with linear relationship; [l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1].
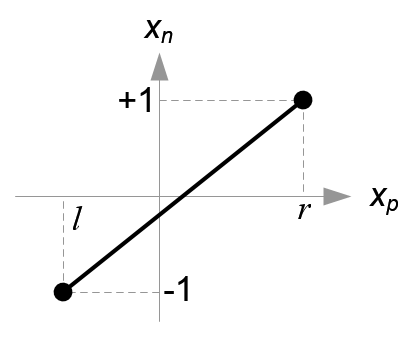
Mapping from xp to xn
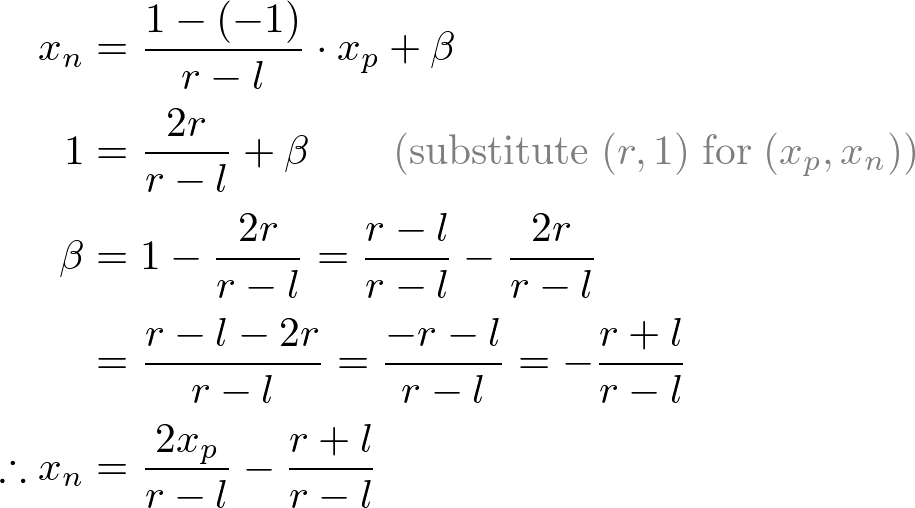
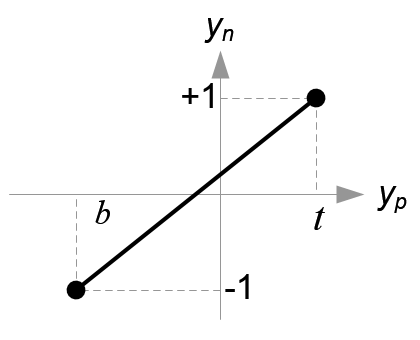
Mapping from yp to yn
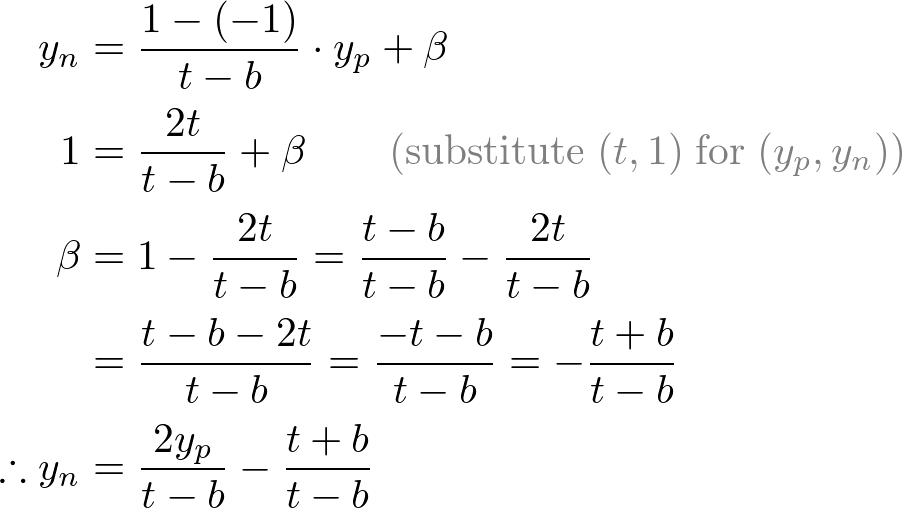
Then, we substitute xp and yp into the above equations.
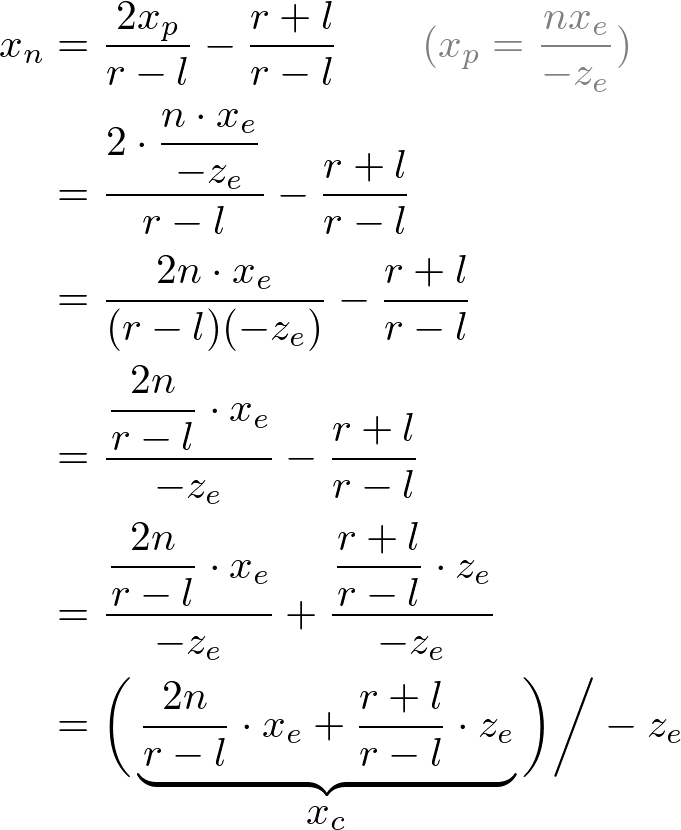
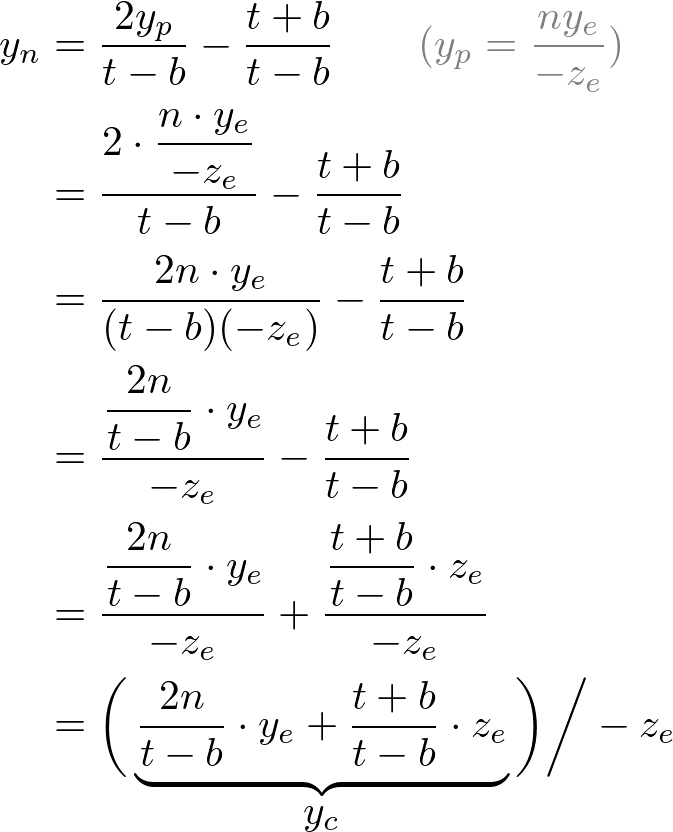
Note that we make both terms of each equation divisible by -ze for perspective division (xc/wc, yc/wc). And we set wc to -ze earlier, and the terms inside parentheses become xc and yc of the clip coordiantes.
From these equations, we can find the 1st and 2nd rows of GL_PROJECTION matrix. 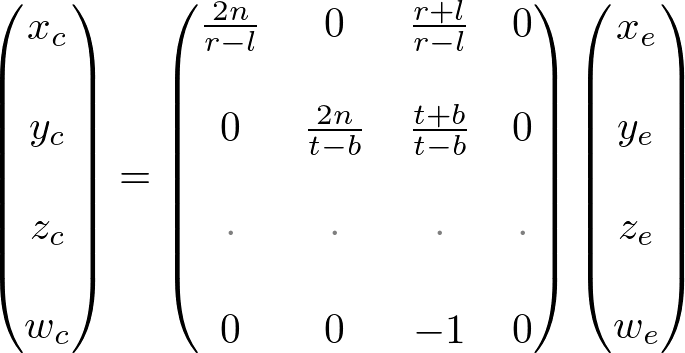
Now, we only have the 3rd row of GL_PROJECTION matrix to solve. Finding zn is a little different from others because ze in eye space is always projected to -n on the near plane. But we need unique z value for the clipping and depth test. Plus, we should be able to unproject (inverse transform) it. Since we know z does not depend on x or y value, we borrow w-component to find the relationship between zn and ze. Therefore, we can specify the 3rd row of GL_PROJECTION matrix like this. 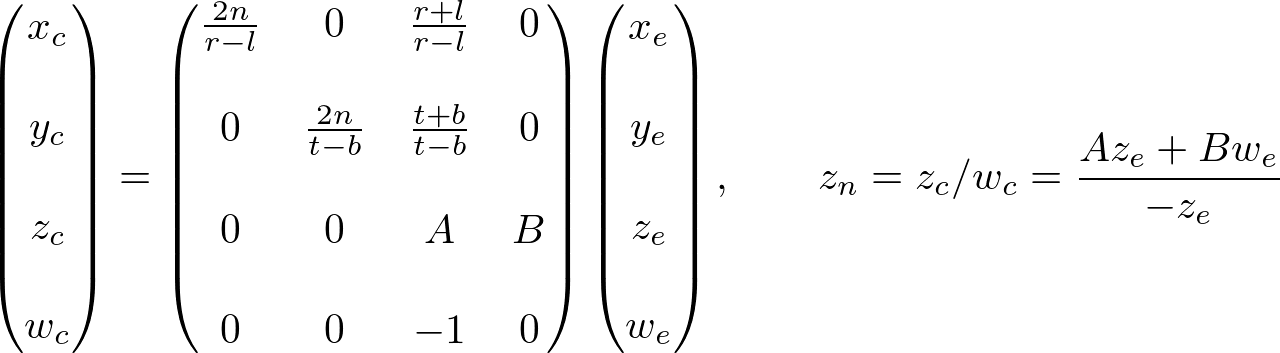
In eye space, we equals to 1. Therefore, the equation becomes; 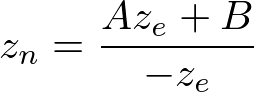
To find the coefficients, A and B, we use the (ze, zn) relation; (-n, -1) and (-f, 1), and put them into the above equation. 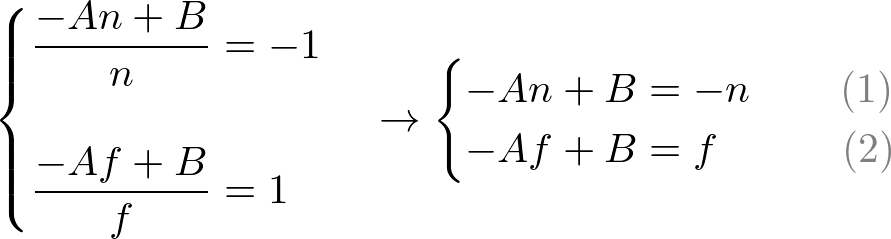
To solve the equations for A and B, rewrite eq.(1) for B; 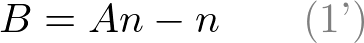
Substitute eq.(1') to B in eq.(2), then solve for A; 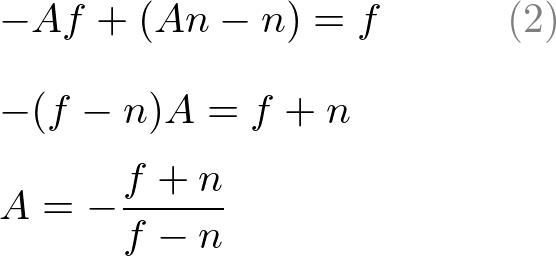
Put A into eq.(1) to find B; 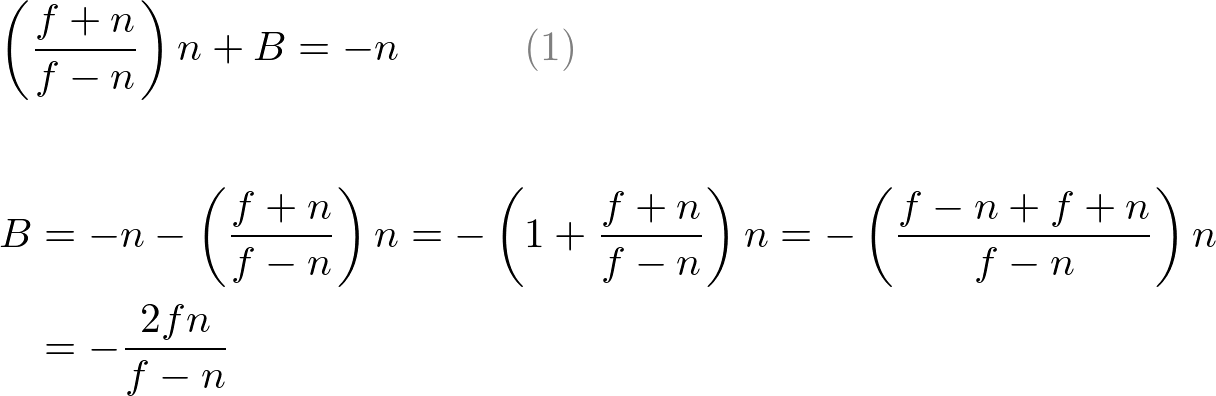
We found A and B. Therefore, the relation between ze and zn becomes; 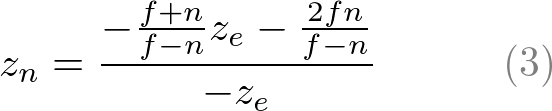
Finally, we found all entries of GL_PROJECTION matrix. The complete projection matrix is; 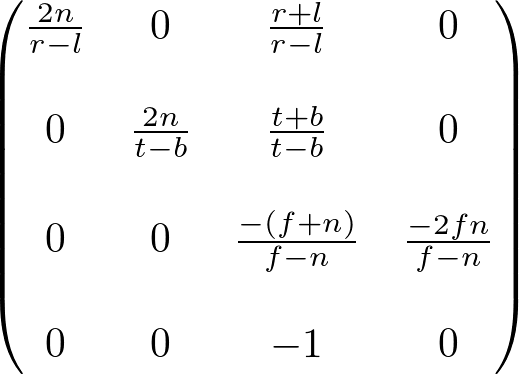
OpenGL Perspective Projection Matrix
This projection matrix is for a general frustum. If the viewing volume is symmetric, which is 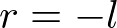 and
and 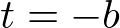 , then it can be simplified as;
, then it can be simplified as; 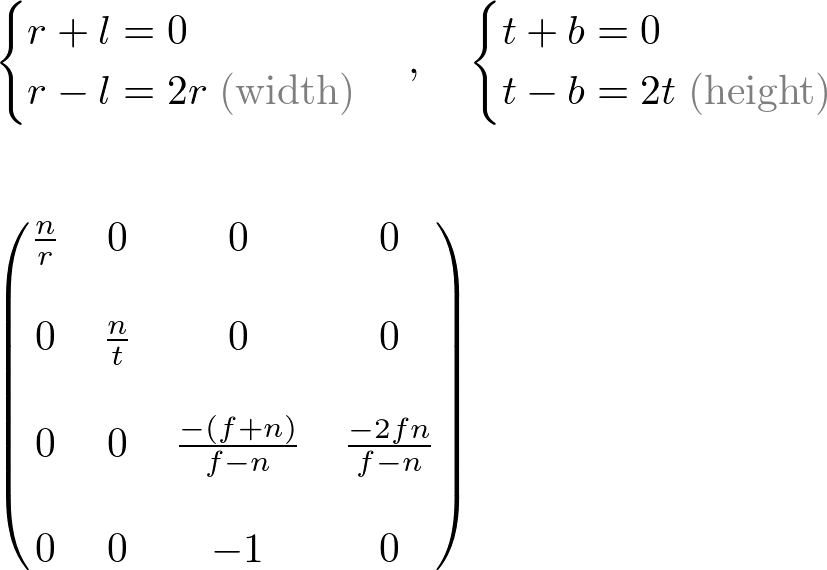
Before we move on, please take a look at the relation between ze and zn, eq.(3) once again. You notice it is a rational function and is non-linear relationship between ze and zn. It means there is very high precision at thenear plane, but very little precision at the far plane. If the range [-n, -f] is getting larger, it causes a depth precision problem (z-fighting); a small change of ze around the far plane does not affect on zn value. The distance between n and f should be short as possible to minimize the depth buffer precision problem.
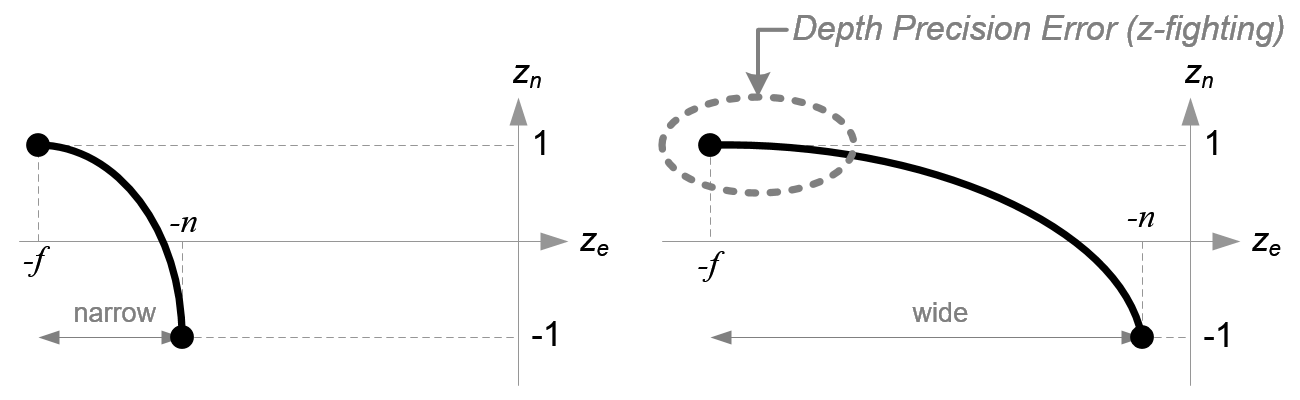
Comparison of Depth Buffer Precisions
Orthographic Projection
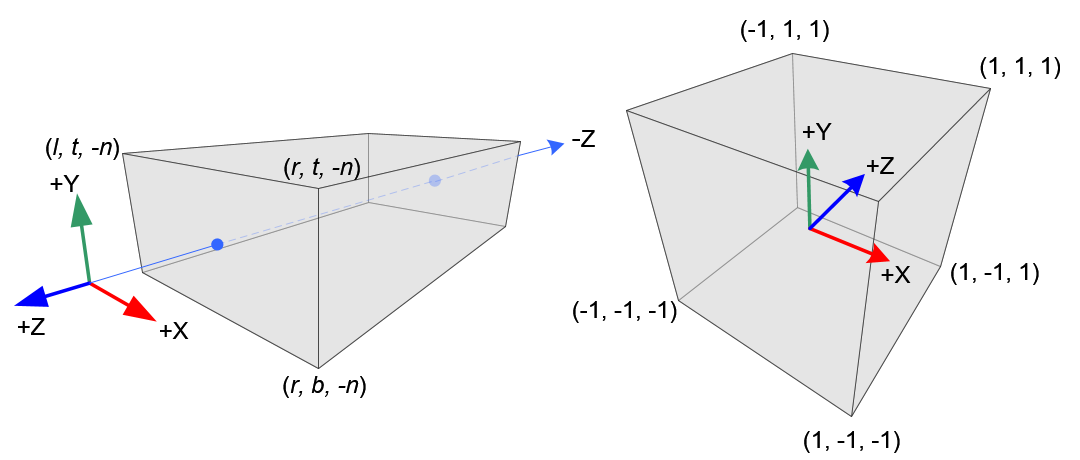
Orthographic Volume and Normalized Device Coordinates (NDC)
Constructing GL_PROJECTION matrix for orthographic projection is much simpler than perspective mode.
All xe, ye and ze components in eye space are linearly mapped to NDC. We just need to scale a rectangular volume to a cube, then move it to the origin. Let's find out the elements of GL_PROJECTION using linear relationship.
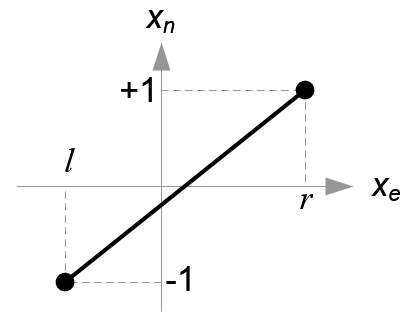
Mapping from xe to xn
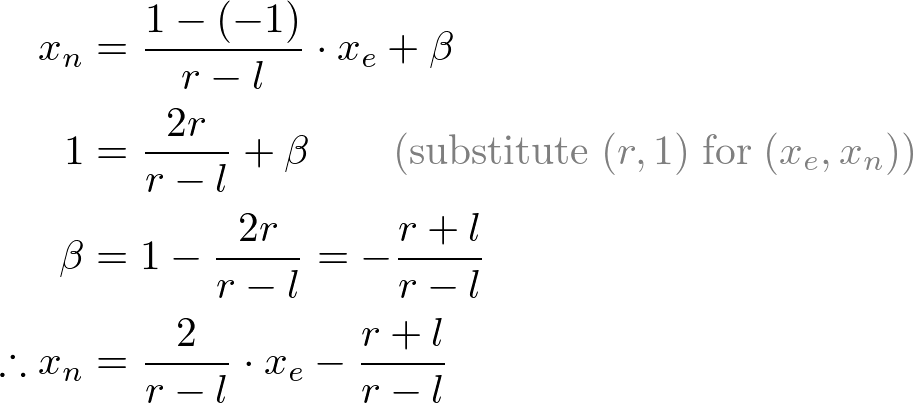
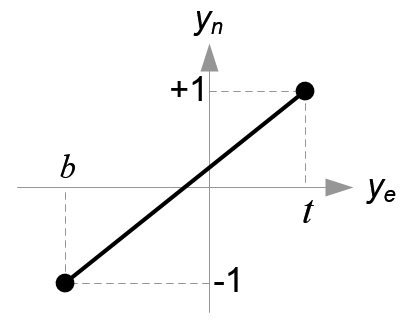
Mapping from ye to yn
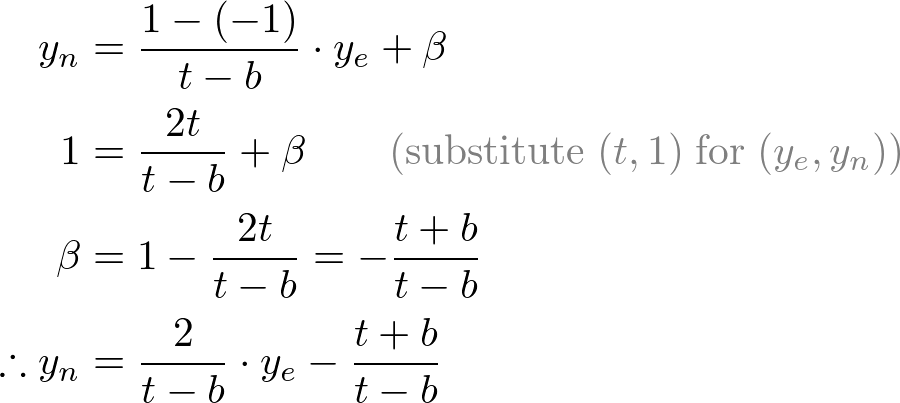
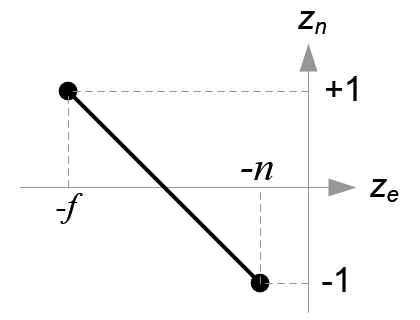
Mapping from ze to zn
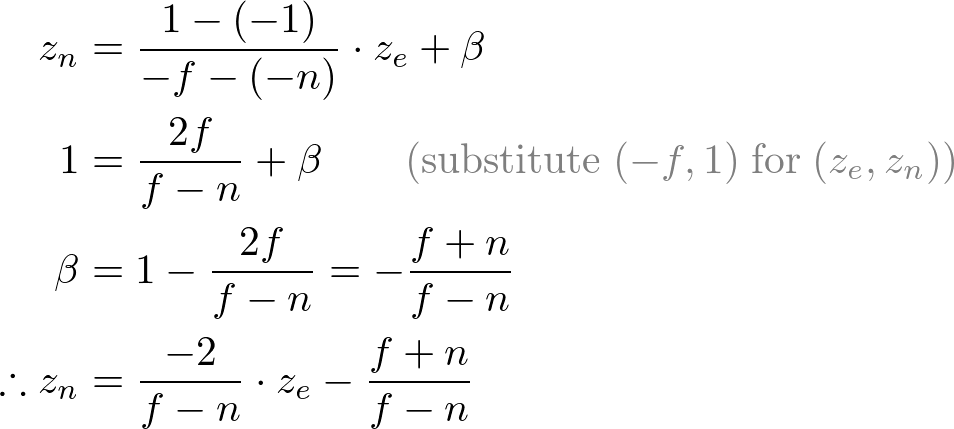
Since w-component is not necessary for orthographic projection, the 4th row of GL_PROJECTION matrix remains as (0, 0, 0, 1). Therefore, the complete GL_PROJECTION matrix for orthographic projection is; 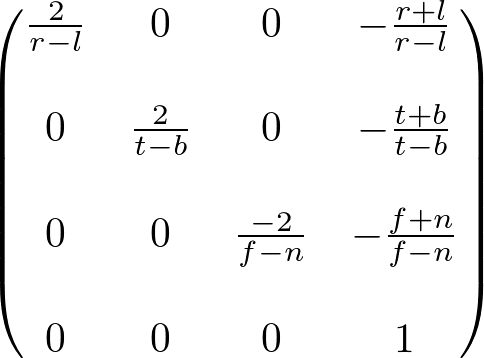
OpenGL Orthographic Projection Matrix
It can be further simplified if the viewing volume is symmetrical, 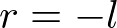 and
and 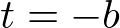 .
. 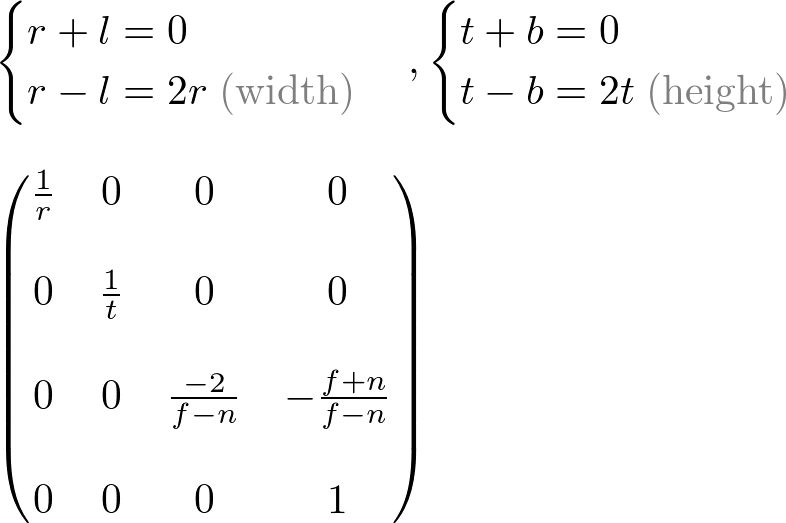
<转载> OpenGL Projection Matrix的更多相关文章
- OpenGL投影矩阵(Projection Matrix)构造方法
(翻译,图片也来自原文) 一.概述 绝大部分计算机的显示器是二维的(a 2D surface).在OpenGL中一个3D场景需要被投影到屏幕上成为一个2D图像(image).这称为投影变换(参见这或这 ...
- 论文阅读笔记(三)【AAAI2017】:Learning Heterogeneous Dictionary Pair with Feature Projection Matrix for Pedestrian Video Retrieval via Single Query Image
Introduction (1)IVPR问题: 根据一张图片从视频中识别出行人的方法称为 image to video person re-id(IVPR) 应用: ① 通过嫌犯照片,从视频中识别出嫌 ...
- OpenGL Column-Major Matrix 使用注意事项
这column major的矩阵是彻底把我搞晕了,以后右乘规则下的矩阵应该这么用 假设我想创建一个2x2的矩阵,数学上我这么写: 1 2 3 4 用代码创建的话这么写 // 按照 row major ...
- Android平台下OpenGL初步
Android OpenGL ES 开发教程 从入门到精通 http://blog.csdn.net/zhoudailiang/article/details/50176143 http://blog ...
- OpenGl从零开始之坐标变换
http://www.tuicool.com/articles/uiayYrI OpenGL学习脚印: 坐标变换过程(vertex transformation) http://blog.csdn.n ...
- OpenGL一些函数详解(二)
OpenGL ES顶点数据绘制技巧 在OpenGL中,绘制一个长方体,需要将每个顶点的坐标放在一个数组中.保存坐标时有一些技巧(由于字母下标不好表示,因此将下标表示为单引号,如A1将在后文中表示为A' ...
- 【GISER && Painter】Chapter00:OpenGL原理学习笔记
说明:简单了解一下OpenGL的工作原理,初步认识计算机对于图形渲染的底层设计与实现,第一次接触,也没学过C艹,欢迎各位批评指正. 一 什么是OpenGL? OpenGL是一个开放标准(specif ...
- OpenGL(6)——坐标系
在掌握基本变换后,学习如何变换coordinate space. 对coordinate space进行变换的目的是将local space中各顶点坐标转换成normalized device coo ...
- GPU相关资料汇总
qemu, quick emulator systemc xilinx qemu nvdla, nvidia deep learning accelerator gpgpu-sim ffgpu ope ...
随机推荐
- study topics
永远不变的东西,原理 study roadmap: 1.user space: tizen power manager => suspend/resume or runtime? android ...
- GLSL语言基础
from http://www.kankanews.com/ICkengine/archives/120870.shtml 变量 GLSL的变量命名方式与C语言类似.变量的名称可以使用字母,数字以及下 ...
- 使用JDBC处理Oracle大数据
一.Oracle中大数据处理 在Oracle中,LOB(Large Object,大型对象)类型的字段现在用得越来越多了.因为这种类型的字段,容量大(最多能容纳4GB的数据),且一个表中可以有多个这种 ...
- 【转】对抗拖库 ―― Web 前端慢加密
0×00 前言 天下武功,唯快不破.但密码加密不同.算法越快,越容易破. 0×01 暴力破解 密码破解,就是把加密后的密码还原成明文密码.似乎有不少方法,但最终都得走一条路:暴力穷举.也许你会说还可以 ...
- VS2008 Windows Form项目安装包生成详解
2008 Windows Form项目的发布对有经验的程序员来说,可能不值一提,但对很多新手来说却不知道如何操作,因为在很多关于Visual Studio的书籍中也没有相关介绍,权威如<C# 2 ...
- XidianOJ 1097 焊板子的xry111
题目描述 我们知道xry111不仅仅代码写的棒,硬件也不是一般人可以比拟的,比如他可以左手右手加上嘴里叼着一个烙铁一起工作,同时焊接三块板子!Orz,现在他的实验室知道他这么厉害了,准备让他焊接N块板 ...
- 问题: ActivityManager: Warning: Activity not started, its current task has been brought to the front
运行程序时看控制台有这样的错误,应用程序没跑起来. 解决办法:project-->Clean
- winform-全局异常捕获作用
using System;using System.Collections.Generic;using System.Linq;using System.Windows.Forms;using Jxs ...
- eval语句(sql)类似asp
执行字符串的SQL语句,相当于asp中的eval ***** declare @sql nvarchar(500) set @sql='select * from sk_hzp_fk_prescri ...
- Python全栈---5.1---装饰器
一.装饰器 执行outer函数,将index作为参数传递, 将outer函数的返回值,重新赋值给index 装饰器可以在函数执行前和执行后执行其他的附加功能,这种在代码运行期间动态增加功能的方式,称之 ...
