基本图像操作和处理(python)

PIL提供了通用的图像处理功能，以及大量的基本图像操作，如图像缩放、裁剪、旋转、颜色转换等。

Matplotlib提供了强大的绘图功能，其下的pylab/pyplot接口包含很多方便用户创建图像的函数。

为了观察和进一步处理图像数据，首先需要加载图像文件，并且为了查看图像数据，我们需要将其绘制出来。

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np

# 加载图像
img = Image.open("tmp.jpg")
# 转为数组
img_data = np.array(img)
# 可视化
plt.imshow(img_data)
plt.show()

对于图像，我们常见的操作有调整图像尺寸，旋转图像以及灰度变换

from PIL import Image
import matplotlib.pyplot as plt

img = Image.open("girl.jpg")

plt.figure()
# 子图
plt.subplot(221)
# 原图
plt.imshow(img)
plt.subplot(222)
# 将图像缩放至 256 * 256
plt.imshow(img.resize((256, 256)))
plt.subplot(223)
# 将图像转为灰度图
plt.imshow(img.convert('L'))
plt.subplot(224)
# 旋转图像
plt.imshow(img.rotate(45))
# 保存图像
plt.savefig("tmp.jpg")
plt.show()

效果演示 ：

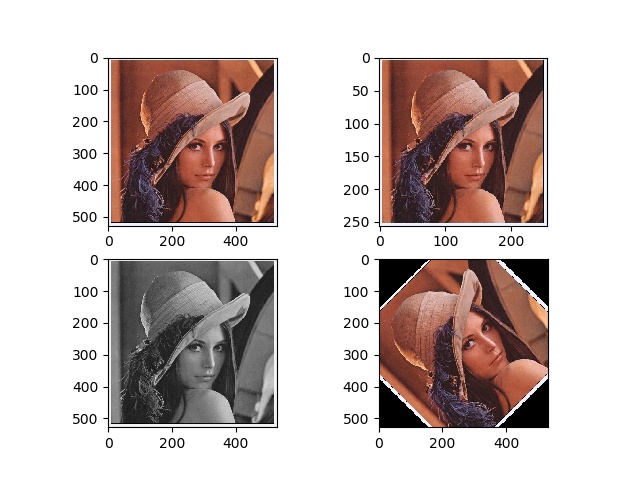
在平常的使用中，绘制图像的轮廓也经常被使用，因为绘制轮廓需要对每个坐标(x, y)的像数值施加同一个阙值，所以需要将图像灰度化

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np

img = Image.open("girl.jpg")

gray_img = np.array(img.convert('L'))
plt.figure()
# 绘制图像灰度化
plt.gray()
# 关闭坐标轴
plt.axis('off')
# 绘制灰度图像
plt.contour(gray_img, origin='image')
plt.figure()
# 绘制直方图,flatten()表示将数组展平
plt.hist(gray_img.flatten(), 128)
plt.show()

轮廓图及直方图：

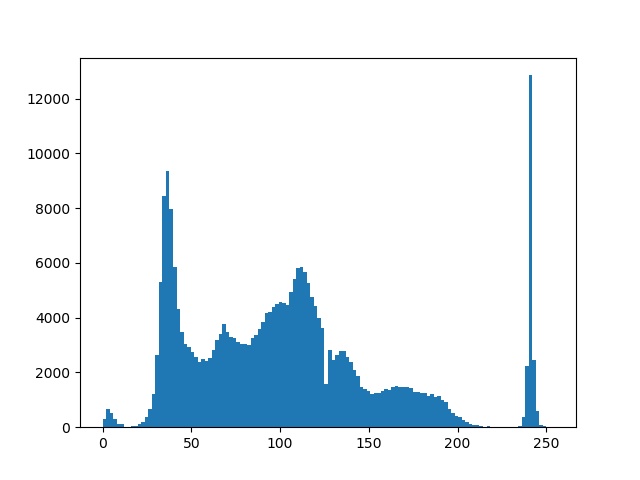
图像的直方图用来表征该图像的像素值的分布情况。用一定数目的小区间来指定表征像素值的范围，每个小区间会得到落入该小区间表示范围的像素数目。hist()函数用于绘制图像的直方图，其只接受一维数组作为第一个参数输入，其第二个参数用于指定小区间的数目。

有时用户需要和应用进行交互，如在一幅图像中标记一些点。Pylab/pyplot库中的ginput()函数就可以实现交互式标注

from PIL import Image
import matplotlib.pyplot as plt

img = Image.open(r"girl.jpg")
plt.imshow(img)
x = plt.ginput(3)
print("clicked point: ", x)

注：该交互在集成编译环境(pyCharm)中如果不能调出交互窗口则无法进行点击，可以在命令窗口下成功执行。

以上我们通过numpy的array()函数将Image对象转换成了数组，以下将展示如何从数组转换成Image对象

from PIL import Image
import numpy as np

img = Image.open(r"girl.jpg")
img_array = np.array(img)
img = Image.fromarray(img_array)

在图像灰度变换中有一个非常有用的例子就是直方图均衡化。直方图均衡化是指将一幅图像的灰度直方图变平，使变换后的图像中每个灰度值的分布概率都相同。直方图均衡化通常是对图像灰度值进行归一化的一个非常好的方法，并且可以增强图像的对比度。

直方图均衡化的变换函数是图像中像素值的累积分布函数(cumulative distribution function，将像素值的范围映射到目标范围的归一化操作)。

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np

def histogram_equalization(img: np, nbr_bins=256):
    imhist, bins = np.histogram(img.flatten())
    cdf = imhist.cumsum() # 累计分布函数
    # 归一化
    cdf = 255 * cdf / cdf[-1]
    # 使用累积分布函数进行线性插值，计算新的像素值
    img2 = np.interp(img.flatten(), bins[:-1], cdf)
    return img2.reshape(img.shape), cdf

img = Image.open(r"girl.jpg").convert('L')
img2, cdf = histogram_equalization(np.array(img))
plt.figure()
plt.gray()
# 绘制子图
plt.subplot(232)
# 变换函数
plt.plot(cdf)
plt.subplot(231)
plt.hist(np.array(img).flatten(), 256)
# 关闭坐标轴，对上一个子图有效
plt.axis('off')
plt.subplot(233)
plt.hist(np.array(img2).flatten(), 256)
plt.axis('off')
plt.subplot(234)
plt.imshow(img)
plt.axis('off')
plt.subplot(236)
plt.imshow(img2)
plt.axis('off')
# 保存绘制图像
plt.savefig("tmp.jpg")
plt.show()

处理结果

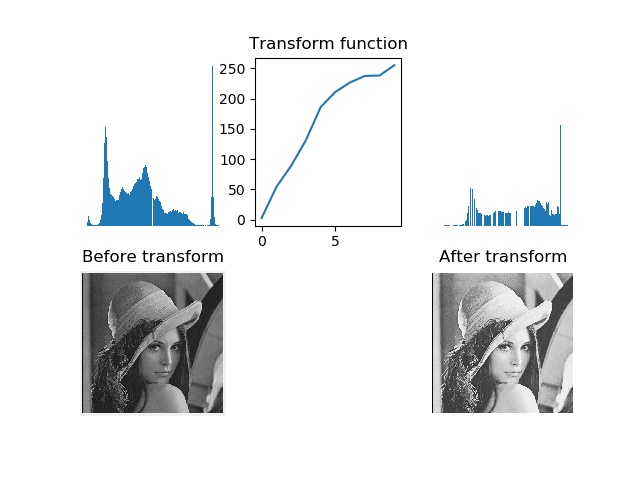
可见，直方图均衡化的图像的对比度增强了，原先图像灰色区域的斜街变得清晰。

PCA(Principal Component Analysis, 主成分分析)是一个非常有用的降维技巧，它可以在使用尽可能少的维数的前提下，尽可能多地保持训练数据的信息。详细介绍及使用见我的另一篇文章：PCA降维

SciPy是建立在Numpy基础上，用于数值运算的开源工具包。Scipy提供很多高效的操作，可以实现数值积分、优化、统计、信号处理，以及对我们来说最为重要的图像处理功能。

图像的高斯模糊是非常经典的图像卷积例子。本质上，图像模糊就是将(灰度)图像 \(I\) 和一个高斯核进行卷积操作：

\[I_\sigma = I * G_\sigma
\]

其中， \(*\) 表示卷积操作；\(G\) 表示标准差为 \(\sigma\) 的二维高斯核，定义为：

\[G_\sigma = \frac{1}{2\pi \sigma^2} e^{-(x^2+y^2) / 2 \sigma^2}
\]

高斯模糊通常是其他图像处理操作的一部分，比如图像插值操作、兴趣点计算以及其他应用。

Scipy有用来做滤波操作的scipy.ndimage.filters模块。该模块使用快速一维分离的方式来计算卷积。使用方式：

from PIL import Image
import numpy as np
from scipy.ndimage import filters

img = Image.open(r"girl.jpg").convert('L')
img = np.array(img)
img2 = filters.gaussian_filter(img, 2)
img3 = filters.gaussian_filter(img, 5)
img4 = filters.gaussian_filter(img, 10)

绘制结果

上面使用的gaussian_filter()函数中的后一个参数表示标准差 \(\sigma\) ，可见随着 \(\sigma\) 的增加，图像变得越来越模糊。 \(\sigma\) 越大，处理后图像细节丢失越多。如果是打算模糊一幅彩色图像，只需要简单地对每一个颜色通道进行高斯模糊：

from PIL import Image
import numpy as np
from scipy.ndimage import filters

img = Image.open(r"girl.jpg")
img = np.array(img)
img2 = np.zeros(img.shape)
for i in range(img2.shape[2]):
    img2[:, :, i] = filters.gaussian_filter(img[:, :, i], 5)
# 将像素值用八位表示
img2 = np.array(img2, 'uint8')

模糊结果：

在很多应用中，图像强度的变化情况是非常重要的，强度的变化可以使用灰度图像的 \(x\) 和 \(y\) 方向导数 \(I_x\) 和 \(I_y\)进行描述

图像的梯度向量为 \(\bigtriangledown I = [I_x, I_y]^T\)。梯度有两个重要属性，一是梯度的大小：

\[| \bigtriangledown I | = \sqrt{I_x^2 + I_y^2}
\]

它描述了图像强度变化的强弱，另一个是图像的角度：

\[\alpha = arctan2(I_x, I_y)
\]

它描述了图像在每个点上强度变化最大的方向。Numpy中的arctan2()函数返回弧度表示的有符号角度，角度的变化区间为 \((-\pi, \pi)\)

可以使用离散近似的方式来计算图像的导数。图像倒数大多数可以通过卷积简单地实现：

\[I_x = I*D_x 和 I_y = I*D_y
\]

对于 \(D_x\) 和 \(D_y\)，通常选择Prewitt滤波器：

\[D_x = \left[
\begin{matrix}
-1 & 0 & 1 \\
-1 & 0 & 1 \\
-1 & 0 & 1
\end{matrix}
\right]
\]

和

\[D_y = \left[
\begin{matrix}
-1 & -1 & -1 \\
0 & 0 & 0 \\
1 & 1 & 1
\end{matrix}
\right]
\]

或者Sobel滤波器

\[D_x = \left[
\begin{matrix}
-1 & 0 & 1 \\
-2 & 0 & 2 \\
-1 & 0 & 1
\end{matrix}
\right]
\]

和

\[D_y = \left[
\begin{matrix}
-1 & -2 & -1 \\
0 & 0 & 0 \\
1 & 2 & 1
\end{matrix}
\right]
\]

这些导数滤波器可以使用scipy.ndimage.filters模块地标准卷积操作来简单地实现

from PIL import Image
import numpy as np
from scipy.ndimage import filters

img = Image.open(r"girl.jpg").convert('L')
img = np.array(img)
imgx = np.zeros(img.shape)
# Sobel导数滤波器
filters.sobel(img, 1, imgx)

imgy = np.zeros(img.shape)
filters.sobel(img, 0, imgy)

magnitude = np.sqrt(imgx**2+imgy**2)

sobel()函数的第二个参数选择 \(x\) 或 \(y\) 方向的导数，第三个参数保存输出变量。在图像中，正导数显示为亮的像素，负导数显示为暗的像素，灰色区域表示导数的值接近零。

上面计算图像导数的方法存在缺陷：在该方法中，滤波器的尺度需要随着图像分辨率的变化而变化(?)。为了在图像噪声方面更稳健，以及在任意尺度上计算导数，我们可以使用高斯导数滤波器：

\[I_x = I * G_{\sigma x} 和 I_y = I*G_{\sigma y}
\]

其中，\(G_{\sigma x}\) 和\(G_{\sigma y}\)表示\(G_\sigma\) 在 \(x\) 和 \(y\) 方向上的导数，\(G_\sigma\) 表示标准差为 \(\sigma\) 的高斯函数。以下给出使用样例：

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
from scipy.ndimage import filters

img = Image.open(r"girl.jpg").convert('L')
img = np.array(img)

sigma = 2
imgx = np.zeros(img.shape)
imgy = np.zeros(img.shape)
filters.gaussian_filter(img, (sigma, sigma), (0, 1), imgx)
filters.gaussian_filter(img, (sigma, sigma), (1, 0), imgy)

magnitude = np.sqrt(imgx**2+imgy**2)

结果演示：

在对图像进行处理时，去噪也是很重要的一环。图像去噪是在去除图像噪声的同时，尽可能地保留图像细节和结构地处理技术，以下给出使用ROF去噪模型地Demo:

from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
from scipy.ndimage import filters

def de_noise(img, U_init, tolerance=0.1, tau=0.125, tv_weight=100):
    U = U_init
    Px = Py = img
    error = 1
    while error > tolerance:
        Uold = U
        # 变量U梯度的x分量
        gradUx = np.roll(U, -1, axis=1)-U
        # 变量U梯度的y分量
        gradUy = np.roll(U, -1, axis=0)-U

        # 更新对偶变量
        PxNew = Px + (tau/tv_weight)*gradUx
        PyNew = Py + (tau/tv_weight)*gradUy
        NormNew = np.maximum(1, np.sqrt(PxNew**2+PyNew**2))

        # 更新x,y分量
        Px = PxNew / NormNew
        Py = PyNew / NormNew

        # 更新原始变量
        RxPx = np.roll(Px, 1, axis=1)  # 将x分量向x轴正方向平移
        RyPy = np.roll(Py, 1, axis=0)  # 将y分量向y轴正方向平移

        DivP = (Px - RxPx) + (Py - RyPy)  # 对偶域散度
        U = img + tv_weight * DivP

        error = np.linalg.norm(U - Uold)/np.sqrt(img.shape[0] * img.shape[1])

        return U, img-U

if __name__ == '__main__':
    im = np.zeros((500, 500))
    im[100:400,100:400] = 128
    im[200:300, 200:300] = 255
    im = im + 30 * np.random.standard_normal((500, 500))

    U, T = de_noise(im, im)
    G = filters.gaussian_filter(im, 10)
    plt.figure()
    plt.gray()
    plt.subplot(221).set_title("Original image")
    plt.axis('off')
    plt.imshow(im)
    plt.subplot(222).set_title("Gauss blurred image")
    plt.axis('off')
    plt.imshow(G)
    plt.subplot(223).set_title("ROF")
    plt.axis('off')
    plt.imshow(U)
    plt.savefig('tmp.jpg')
    plt.show()

结果演示

ROF去噪后的图像保留了边缘和图像的结构信息，同时模糊了“噪声”。

np.roll()函数可以循环滚动元素，np.linalg.norm()用于衡量两个数组间的差异。

之后有空将补充图像去噪

参考书籍

Python计算机视觉