leadcode的Hot100系列--17. 电话号码的字母组合--回溯的另一种想法的应用

提交leetcode的时候遇到了问题，一直说访问越界，但仔仔细细检查n多遍，就是检查不出来。

因为我用到了count全局变量，自加一来表明当前数组访问的位置，

后来突然想到，是不是在leetcode在运行测试用例的时候，是连续测试的，用的同一个上下文，这样的话，就没有对这个全局变量清零……

果然，清零之后就可以了……已经3:47了，这里先上代码，明天再详细说吧……

---

今天更新一下这道题的思路。

可以先参考一下之前的两篇文章，循序渐进，好理解一些：

leadcode的Hot100系列--78. 子集--位运算

leadcode的Hot100系列--78. 子集--回溯

在 子集--回溯 的文章里面，介绍了一下数字的排列组合，用01来表示对应的数字是否存在。

如果我们还是按照这个思路，但是换一个想法呢？

0、1是不是本身就可以代表着字符串？

对应排列出来的000\001\010 ... 是不是就是相当于：

我需要一个数字组合，组合需要三位数，每一位的数字要么是0，要么是1。

这么一想，是不是就与题目一致了：

我需要一个字母组合，组合的位数就是输入的字符串长度，每一位的字母是对应的几个字母中的某一个。

对，就是这么想的，比如，输入“89”，就说明，字母组合的位数是两位，第一位字母是'tuv'里面的一个，第二位字母是'wxyz'里面的一个。

这里再看下之前上一篇中回溯的代码：

void backtrack (int t)
{
    if (t == level)
        show();
    else
        for (int i=0;i<=1;i++)
        {
            y[t]=i;
            backtrack(t+1);
        }
}

重点来了！！！！

• 第三行的level表示层数，也就是遍历的深度，也就是组合所需要的位数，当需要两位字母的时候，就只要两层。
• 第六行的for循环，表示了每一层的选项，之前因为只需要表示存在和不存在，所以只需要用0和1就够了，但在这里，是由数字对应的字符串的某一个，例如如果数字是8，则对应的选项就是't'和'u'和'v'。

所以，当输入为“89”的时候，就可以生成这样一种树：

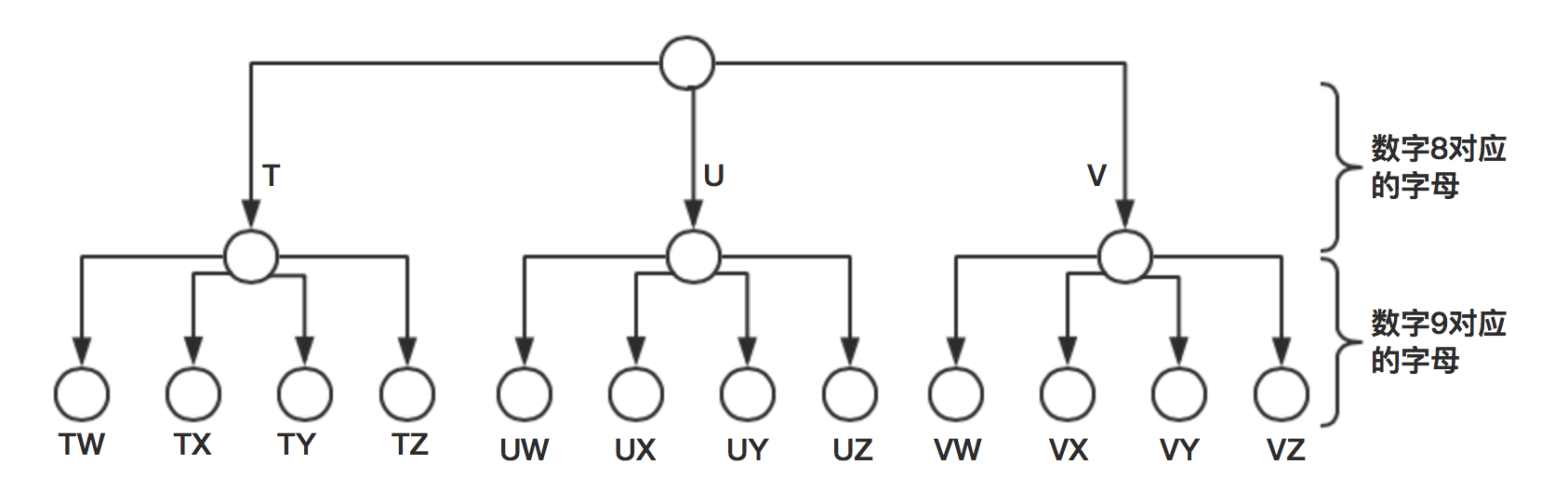
控制了树的层数和树的分支（分支就是可选项）之后，就可以完成所有组合。

char table[][5] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
char level = 0;
char *p[8];   // 指向数字对应的字符串，例如，当输入数字为"89"时,p[0]为"tuv",p[1]为"wxyz"。
char len[8];  // 对应上面p存储的字符串的长度，例如，当输入数字为"89"是，len[0]=3,len[1]=4。
char **out; //二维数组，是最终输出
int count = 0; // 用来记录当前已经生成了几个组合，对应着out数组的行坐标
char y[8] = {0}; // 记录每一次的组合结果

void backtrack(int level_now)
{
    if (level_now == level)
    {
        memcpy(out[count], y, level);  // 把这次组合结果拷贝到out数组中。这里为什么需要用一个y数组来记录组合结果，然后拷贝到out中呢？大家可以自己想一想
        count ++;   // 完成一个字符串
        return;
    }
    for (int i=0; i<len[level_now]; i++)
    {
        y[level_now] = p[level_now][i];
        backtrack(level_now+1);
    }
    return;
}

char ** letterCombinations(char * digits, int* returnSize){
    level = strlen(digits);  // 遍历的层数
    *returnSize = 0;
    if (0 == level) return NULL;

    *returnSize = 1;

    for(int i=0; i<level; i++)
    {
        p[i] = table[digits[i]-'0'];  // 对p数组进行赋值
        len[i] = strlen(p[i]);
        if (len[i] == 0)
        {
            *returnSize = 0;
            return NULL;
        }
        *returnSize *= len[i];    // 计算总共有多少个组合
    }
    out = (char **)calloc(*returnSize, sizeof(char *));  // 先分配行指针
    if (NULL == out) return NULL;
    for (int i=0; i<*returnSize; i++)
    {
        out[i] = (char *)calloc(1, sizeof(char) * (level+1));  // 再分配每个行指针的内容，因为字符串后面需要一个结束符'\0'，所以这里需要level+1
        if (NULL == out[i]) return NULL;
    }
    backtrack(0);
    count = 0;   // 这里很重要！很重要！！很重要！！！
    return out;
}