算法详解之最近公共祖先(LCA)

若图片出锅请转至here

概念

首先是最近公共祖先的概念(什么是最近公共祖先？)：

在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。

换句话说，就是两个点在这棵树上距离最近的公共祖先节点。

所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。

有人可能会问：那他本身或者其父亲节点是否可以作为祖先节点呢？

答案是肯定的，很简单，按照人的亲戚观念来说，你的父亲也是你的祖先，而LCA还可以将自己视为祖先节点。

举个例子吧，如下图所示4和5的最近公共祖先是2，5和3的最近公共祖先是1，2和1的最近公共祖先是1。　

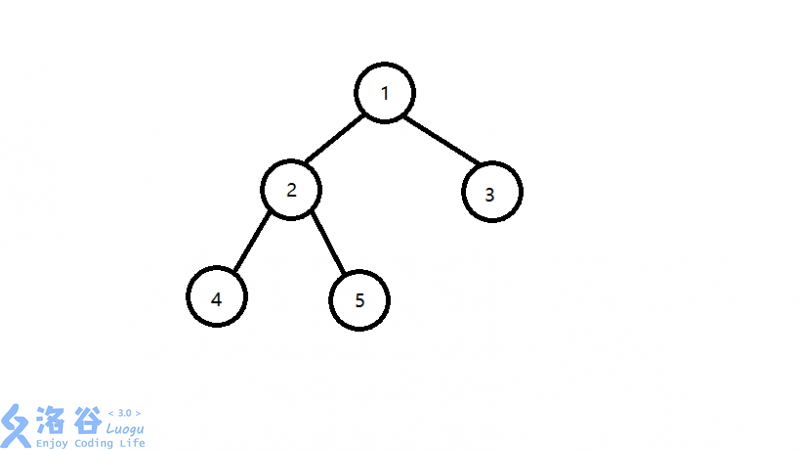
这就是最近公共祖先的基本概念了，那么我们该如何去求这个最近公共祖先呢？

通常初学者都会想到最简单粗暴的一个办法：对于每个询问，遍历所有的点，时间复杂度为\(O(n*q)\) ，很明显，n和q一般不会很小。

怎么办办？

LCA其实有很多种解法，这里介绍几个

一、Tarjan大法好！

什么是Tarjan(离线)算法呢？顾名思义，就是在一次遍历中把所有询问一次性解决，所以其时间复杂度是\(O(n+q)\)。

Tarjan算法的优点在于相对稳定，时间复杂度也比较居中，也很容易理解。

下面详细介绍一下Tarjan算法的基本思路：

1. 任选一个点为根节点，从根节点开始。

2. 遍历该点u所有子节点v，并标记这些子节点v已被访问过。

3. 若是v还有子节点，返回2，否则下一步。

4. 合并v到u上。

5. 寻找与当前点u有询问关系的点v。

6. 若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

遍历的话需要用到dfs来遍历(相信来看的人都懂吧...)，至于合并，最优化的方式就是利用并查集来合并两个节点。

• 伪代码

Tarjan(u)//marge和find为并查集合并函数和查找函数
{
    for each(u,v)    //访问所有u子节点v
    {
        Tarjan(v);        //继续往下遍历
        marge(u,v);    //合并v到u上
        标记v被访问过;
    }
    for each(u,e)    //访问所有和u有询问关系的e
    {
        如果e被访问过;
        u,e的最近公共祖先为find(e);
    }
}

个人感觉这样还是有很多人不太理解，所以打算模拟一遍给大家看。

假设我们有一组数据 9个节点 8条边 联通情况如下：

1--2，1--3，2--4，2--5，3--6，5--7，5--8，7--9 即下图所示的树

设我们要查找最近公共祖先的点为9--8，4--6，7--5，5--3；

设f[]数组为并查集的父亲节点数组，初始化f[i]=i，vis[]数组为是否访问过的数组，初始为0;　

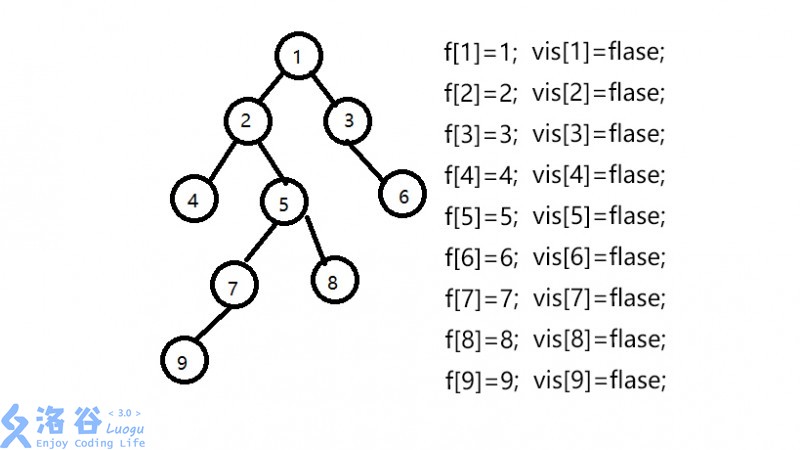
下面开始模拟过程：

取1为根节点，往下搜索发现有两个儿子2和3；

先搜2，发现2有两个儿子4和5，先搜索4，发现4没有子节点，则寻找与其有关系的点；

发现6与4有关系，但是vis[6]=0，即6还没被搜过，所以不操作；

发现没有和4有询问关系的点了，返回此前一次搜索，更新vis[4]=1；

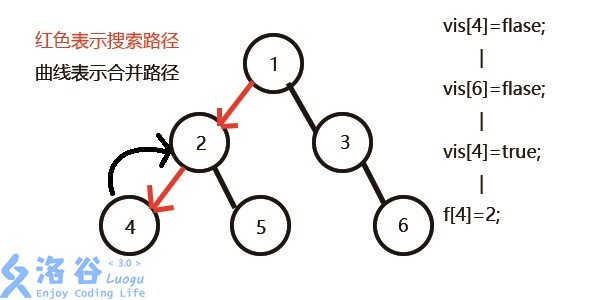
表示4已经被搜完，更新f[4]=2，继续搜5，发现5有两个儿子7和8;

先搜7，发现7有一个子节点9，搜索9，发现没有子节点，寻找与其有关系的点；

发现8和9有关系，但是vis[8]=0,即8没被搜到过，所以不操作；

发现没有和9有询问关系的点了，返回此前一次搜索，更新vis[9]=1；

表示9已经被搜完，更新f[9]=7，发现7没有没被搜过的子节点了，寻找与其有关系的点；

发现5和7有关系，但是vis[5]=0，所以不操作；

发现没有和7有关系的点了，返回此前一次搜索，更新vis[7]=1；

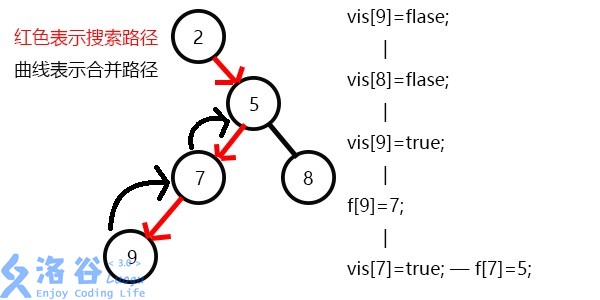
表示7已经被搜完，更新f[7]=5，继续搜8，发现8没有子节点，则寻找与其有关系的点；

发现9与8有关系，此时vis[9]=1，则他们的最近公共祖先为find(9)=5；

(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)

发现没有与8有关系的点了，返回此前一次搜索，更新vis[8]=1；

表示8已经被搜完，更新f[8]=5，发现5没有没搜过的子节点了，寻找与其有关系的点；

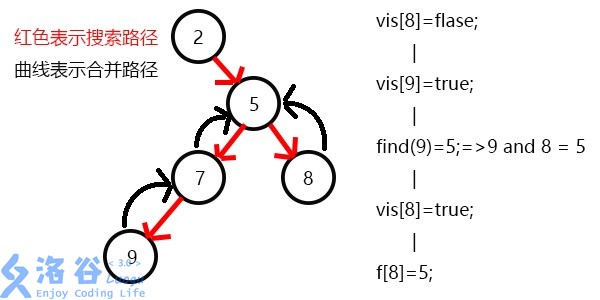
发现7和5有关系，此时vis[7]=1，所以他们的最近公共祖先为find(7)=5；

(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)

又发现5和3有关系，但是vis[3]=0，所以不操作，此时5的子节点全部搜完了；

返回此前一次搜索，更新vis[5]=1，表示5已经被搜完，更新f[5]=2；

发现2没有未被搜完的子节点，寻找与其有关系的点；

又发现没有和2有关系的点，则此前一次搜索，更新vis[2]=1；

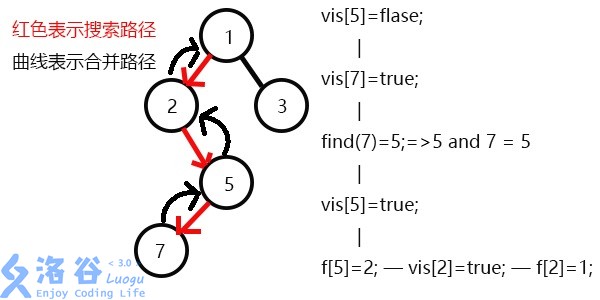
表示2已经被搜完，更新f[2]=1，继续搜3，发现3有一个子节点6；

搜索6，发现6没有子节点，则寻找与6有关系的点，发现4和6有关系；

此时vis[4]=1，所以它们的最近公共祖先为find(4)=1;

(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)

发现没有与6有关系的点了，返回此前一次搜索，更新vis[6]=1，表示6已经被搜完了；

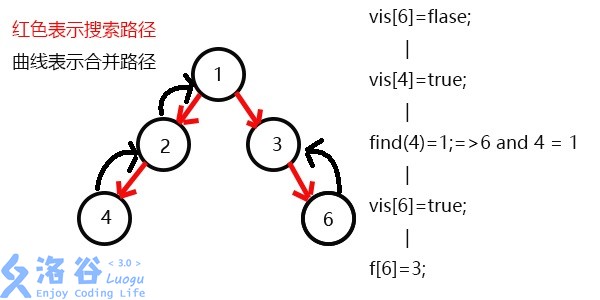
更新f[6]=3，发现3没有没被搜过的子节点了，则寻找与3有关系的点；

发现5和3有关系，此时vis[5]=1，则它们的最近公共祖先为find(5)=1；

(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)

发现没有和3有关系的点了，返回此前一次搜索，更新vis[3]=；

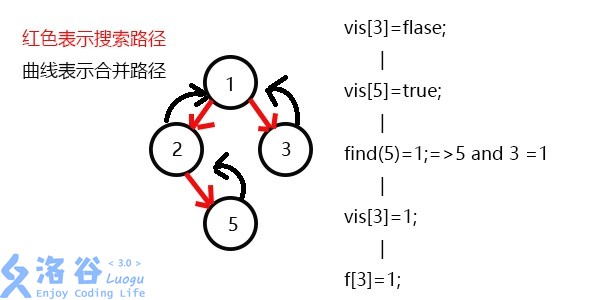
更新f[3]=1，发现1没有被搜过的子节点也没有有关系的点，此时可以退出整个dfs了。

经过这次dfs我们得出了所有的答案，有没有觉得很神奇呢？是否对Tarjan算法有更深层次的理解了呢？

二、倍增LCA

何为倍增？

所谓倍增，就是按\(2\)的倍数来增大，也就是跳 \(1,2,4,8,16,32……\) 不过在这我们不是按从小到大跳，而是从大向小跳，即按\(……32,16,8,4,2,1\)来跳，如果大的跳不过去，再把它调小。这是因为从小开始跳，可能会出现“悔棋”的现象。拿 55 为例，从小向大跳，\(5≠1+2+4\),所以我们还要回溯一步，然后才能得出\(5=1+4\)；而从大向小跳，直接可以得出\(5=4+1\)。这也可以拿二进制为例，\(5(101)\)，从高位向低位填很简单，如果填了这位之后比原数大了，那我就不填，这个过程是很好操作的。

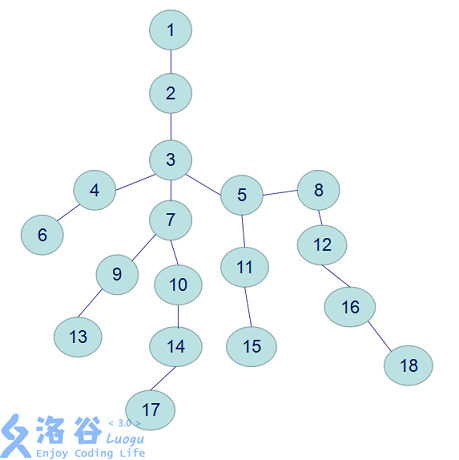
这里以编号为17和18结点为例

\(17->3\)

\(18->5->3\)

可以看出向上跳的次数大大减小。这个算法的时间复杂度为\(O(nlogn)\),已经可以满足大部分的需求。

想要实现这个算法，首先我们要记录各个点的深度和他们\(2^i\)级的的祖先，用数组\(\rm{deep}\)表示每个节点的深度，\(fa[i][j]\)表示节点\(i\)的\(2^j\)级祖先。 代码如下：

inline void getdeep(int now,int father)//now表示当前节点，father表示它的父亲节点
{
	deep[now]=deep[father]+1;
	fa[now][0]=father;
	for(int i=1;(1<<i)<=deep[now];i++)
		fa[now][i]=fa[fa[now][i-1]][i-1];//这个转移可以说是算法的核心之一
						//意思是f的2^i祖先等于f的2^(i-1)祖先的2^(i-1)祖先
						//2^i=2^(i-1)+2^(i-1)
	for(int i=head[now];i;i=edge[i].next)//注意：尽量用链式前向星来存边，速度会大大提升
	{
		if(edge[i].to==father)continue;
		getdeep(edge[i].to,now);
	}
}

然后我们要算出log2n

log2n=log(n)/log(2)+0.5;

接下来就是倍增LCA了，我们先把两个点提到同一高度，再统一开始跳。

但我们在跳的时候不能直接跳到它们的LCA，因为这可能会误判，比如\(4\)和\(8\)，在跳的时候，我们可能会认为\(1\)是它们的LCA，但\(1\)只是它们的祖先，它们的LCA其实是\(3\)。所以我们要跳到它们LCA的下面一层，比如\(4\)和\(8\)，我们就跳到\(4\)和\(5\)，然后输出它们的父节点，这样就不会误判了。

inline int lca(int u,int v)
{
	int deepu=deep[u],deepv=deep[v];
	if(deepu!=deepv)//先跳到同一深度
	{
		if(deep[u]<deep[v])
		{
			swap(u,v);
			swap(deepu,deepv);
		}
		int d=deepu-deepv;
		for(int i=0;i<=log2n;i++)
			if((1<<i)&d)u=fa[u][i];
	}
	if(u==v)return u;
	for(int i=log2n;i>=0;i--)
	{
		if(deep[fa[u][i]]<=0)continue;
		if(fa[u][i]==fa[v][i])continue;
		else u=fa[u][i],v=fa[v][i];//因为我们要跳到它们LCA的下面一层，所以它们肯定不相等，如果不相等就跳过去。
	}
	return fa[u][0];
}

完整的求17和18的LCA的路径：

\(17->10->7->3\)

\(18->16->8->5->3\)

解释：首先，\(18\)要跳到和\(17\)深度相同，然后\(18\)和\(17\)一起向上跳，一直跳到LCA的下一层(\(17\)是\(7\)，\(18\)是\(5\))，此时LCA就是它们的父亲

总体来说就是这样了;

参考博文:https://www.cnblogs.com/jvxie/p/4854719.html

参考博文:https://www.luogu.org/blog/morslin/solution-p3379