Dijkstra算法详细(单源最短路径算法)

介绍

对于dijkstra算法，很多人可能感觉熟悉而又陌生，可能大部分人比较了解bfs和dfs，而对dijkstra和floyd算法可能知道大概是图论中的某个算法，但是可能不清楚其中的作用和原理，又或许，你曾经感觉它很难，那么，这个时候正适合你重新认识它。

Dijkstra能是干啥的？

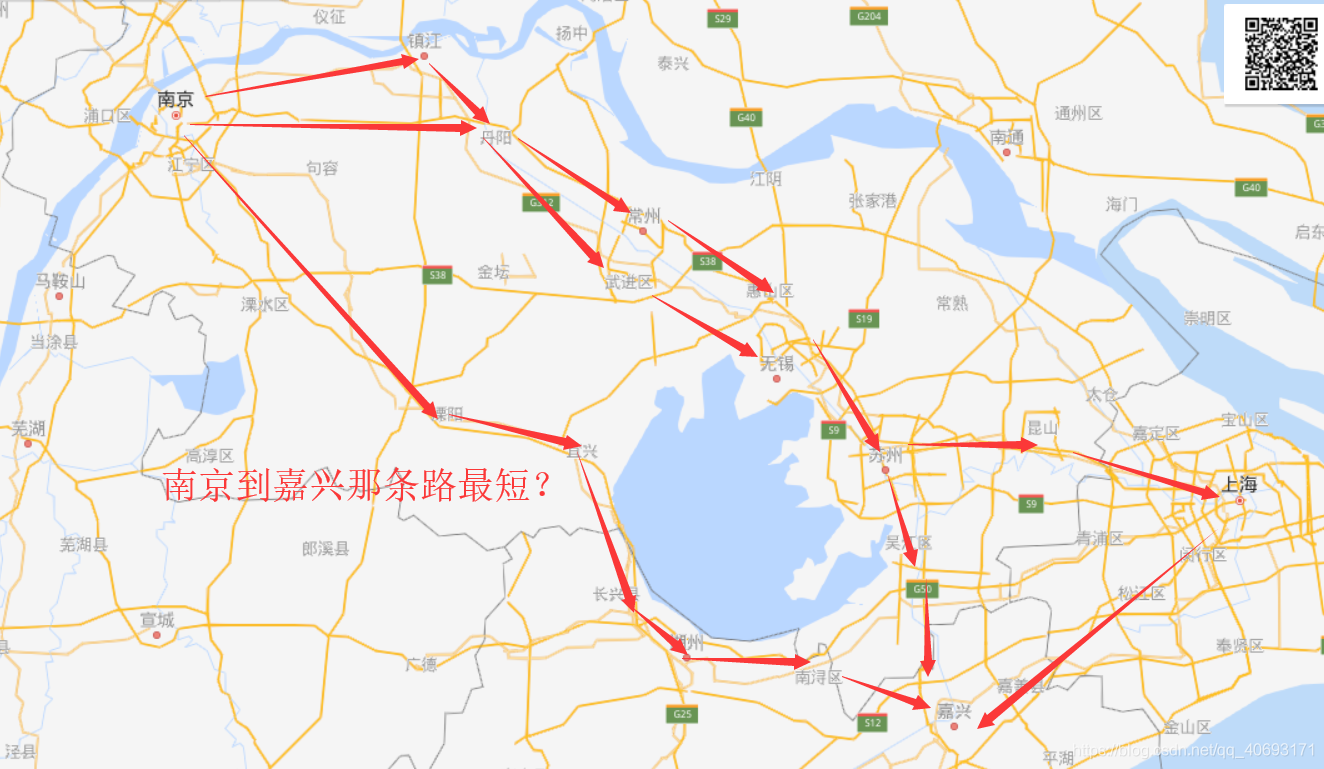
Dijkstra是用来求单源最短路径的

就拿上图来说，假如直到的路径和长度已知，那么可以使用dijkstra算法计算南京到图中所有节点的最短距离。

单源什么意思？

• 从一个顶点出发，Dijkstra算法只能求一个顶点到其他点的最短距离而不能任意两点。

和bfs求的最短路径有什么区别？

• bfs求的与其说是路径，不如说是次数。因为bfs他是按照队列一次一次进行加入相邻的点，而两点之间没有权值或者权值相等(代价相同)。处理的更多是偏向迷宫类的这种都是只能走邻居(不排除特例)。

Dijkstra在处理具体实例的应用还是很多的，因为具体的问题其实带权更多一些。

比如一个城市有多个乡镇，乡镇可能有道路，也可能没有，整个乡镇联通，如果想计算每个乡镇到ａ镇的最短路径，那么Dijkstra就派上了用场。

算法分析

对于一个算法，首先要理解它的运行流程。

对于一个Dijkstra算法而言，前提是它的前提条件和环境：

• 一个连通图，若干节点，节点可能有数值，但是路径一定有权值。并且路径不能为负。否则Dijkstra就不适用。

Dijkstra的核心思想是贪心算法的思想。不懂贪心？

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

对于贪心算法，在很多情况都能用到。下面举几个不恰当的例子！

打个比方，吃自助餐，目标是吃回本，那么胃有限那么每次都仅最贵的吃。

上学时，麻麻说只能带5个苹果，你想带最多，那么选五个苹果你每次都选最大的那个五次下来你就选的最重的那个。

不难发现上面的策略虽然没有很强的理论数学依据，或者不太好说明。但是事实规律就是那样，并且对于贪心问题大部分都需要排序,还可能会遇到类排序。并且一个物体可能有多个属性，不同问题需要按照不同属性进行排序，操作。

那么我们的Dijkstra是如何贪心的呢？对于一个点，求图中所有点的最短路径，如果没有正确的方法胡乱想确实很难算出来，并且如果暴力匹配复杂度呈指数级上升不适合解决实际问题。

那么我们该怎么想呢？

Dijkstra算法的前提：

1. 首先，Dijkstra处理的是带正权值的有权图，那么，就需要一个二维数组（如果空间大用list数组）存储各个点到达(边)的权值大小。(邻接矩阵或者邻接表存储)
2. 其次，还需要一个boolean数组判断那些点已经确定最短长度，那些点没有确定。int数组记录距离(在算法执行过程可能被多次更新)。
3. 需要优先队列加入已经确定点的周围点。每次抛出确定最短路径的那个并且确定最短，直到所有点路径确定最短为止。

简单的概括流程为：

• 一般从选定点开始抛入优先队列。（路径一般为0），boolean数组标记0的位置(最短为0) , 然后0周围连通的点抛入优先队列中（可能是node类），并把各个点的距离记录到对应数组内(如果小于就更新，大于就不动，初始第一次是无穷肯定会更新)，第一次就结束了
• 从队列中抛出距离最近的那个点B（第一次就是0周围邻居）。这个点距离一定是最近的（所有权值都是正的，点的距离只能越来越长。）标记这个点为true，并且将这个点的邻居加入队列(下一次确定的最短点在前面未确定和这个点邻居中产生),并更新通过B点计算各个位置的长度，如果小于则更新！
  
  
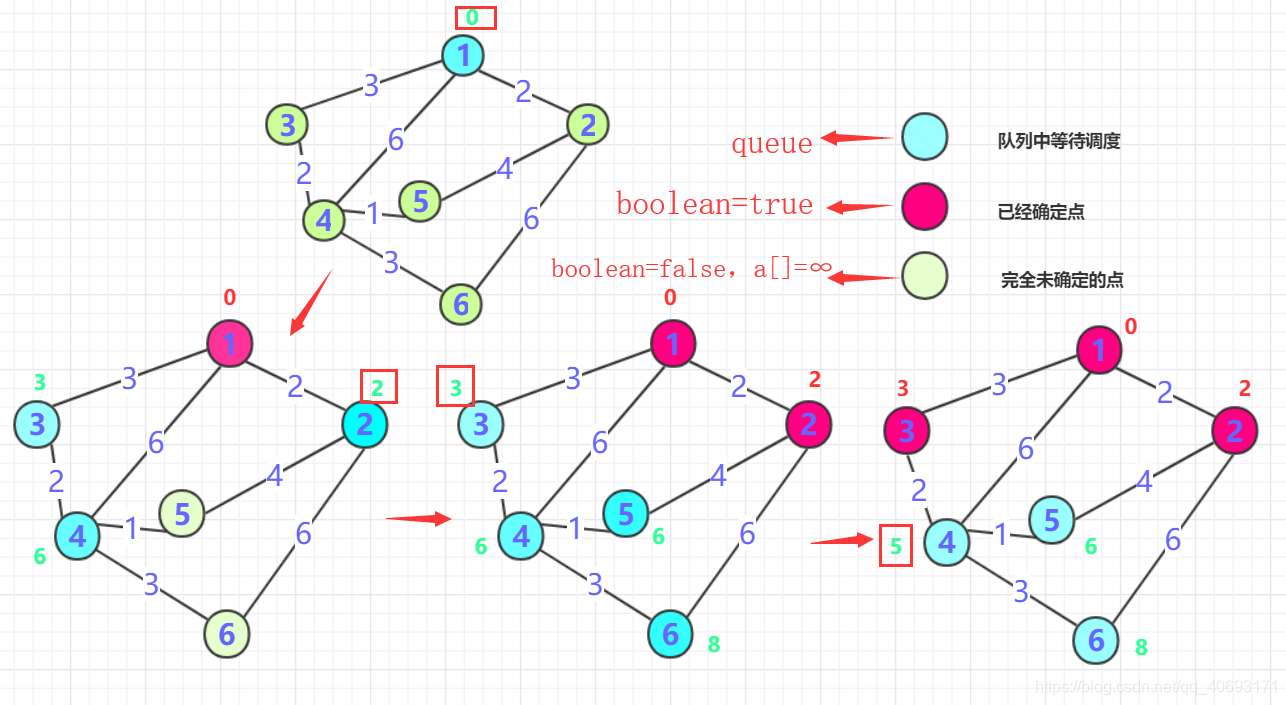
• 重复二的操作，直到所有点都确定。
  
  

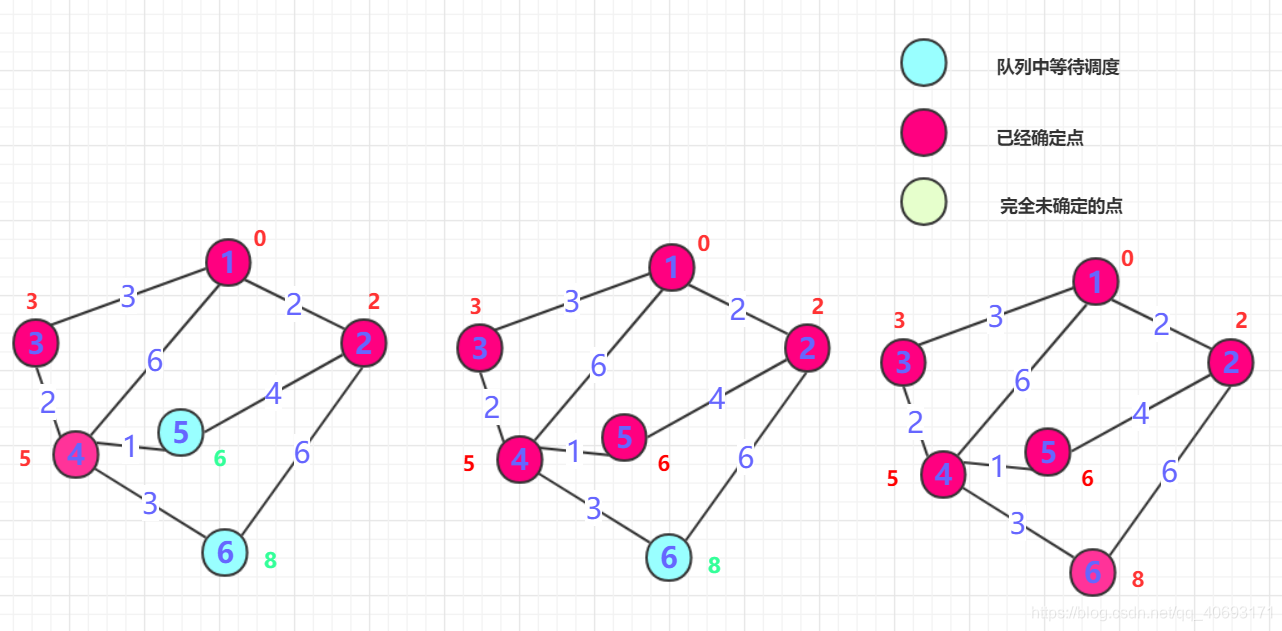
算法实现

package 图论;

import java.util.ArrayDeque;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;

public class dijkstra {
	static class node
	{
		int x; //节点编号
		int lenth;//长度
		public node(int x,int lenth) {
			this.x=x;
			this.lenth=lenth;
		}
	}

	public static void main(String[] args) {

		int[][] map = new int[6][6];//记录权值，顺便记录链接情况，可以考虑附加邻接表
		initmap(map);//初始化
		boolean bool[]=new boolean[6];//判断是否已经确定
		int len[]=new int[6];//长度
		for(int i=0;i<6;i++)
		{
			len[i]=Integer.MAX_VALUE;
		}
		Queue<node>q1=new PriorityQueue<node>(com);
		len[0]=0;//从0这个点开始
		q1.add(new node(0, 0));
		int count=0;//计算执行了几次dijkstra
		while (!q1.isEmpty()) {
			node t1=q1.poll();
			int index=t1.x;//节点编号
			int length=t1.lenth;//节点当前点距离
			bool[index]=true;//抛出的点确定
			count++;//其实执行了6次就可以确定就不需要继续执行了  这句可有可无，有了减少计算次数
			for(int i=0;i<map[index].length;i++)
			{
				if(map[index][i]>0&&!bool[i])
				{
					node node=new node(i, length+map[index][i]);
					if(len[i]>node.lenth)//需要更新节点的时候更新节点并加入队列
					{
						len[i]=node.lenth;
						q1.add(node);
					}
				}
			}
		}
		for(int i=0;i<6;i++)
		{
			System.out.println(len[i]);
		}
	}
	static Comparator<node>com=new Comparator<node>() {

		public int compare(node o1, node o2) {
			return o1.lenth-o2.lenth;
		}
	};

	private static void initmap(int[][] map) {
		map[0][1]=2;map[0][2]=3;map[0][3]=6;
		map[1][0]=2;map[1][4]=4;map[1][5]=6;
		map[2][0]=3;map[2][3]=2;
		map[3][0]=6;map[3][2]=2;map[3][4]=1;map[3][5]=3;
		map[4][1]=4;map[4][3]=1;
		map[5][1]=6;map[5][3]=3;
	}
}

执行结果：



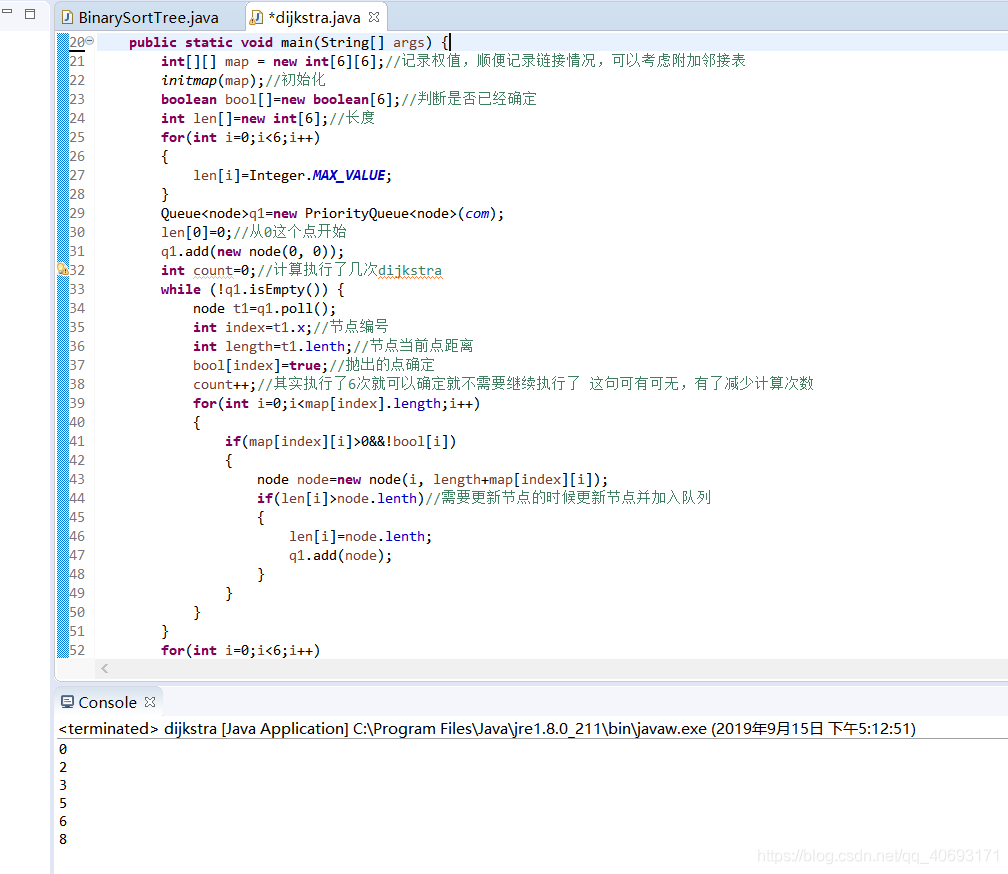
当然，dijkstra算法比较灵活，实现方式也可能有点区别，但是思想是不变的：一个贪心思路。dijkstra执行一次就能够确定一个点，所以只需要执行点的总和次数即可完成整个算法。

欢迎感谢小伙伴点赞、关注，赠人玫瑰，手有余香！蟹蟹！