「面试高频」二叉搜索树&双指针&贪心 算法题指北

---

本文将覆盖 「字符串处理」 + 「动态规划」 方面的面试算法题，文中我将给出：

1. 面试中的题目
2. 解题的思路
3. 特定问题的技巧和注意事项
4. 考察的知识点及其概念
5. 详细的代码和解析

开始之前，我们先看下会有哪些重点案例：

为了方便大家跟进学习，我在 GitHub 建立了一个仓库

仓库地址：超级干货！精心归纳视频、归类、总结，各位路过的老铁支持一下！给个 Star ！

现在就让我们开始吧！

---

二叉搜索树

二叉搜索树（Binary Search Tree），它或者是一棵空树，或者是具有下列性质的二叉树：

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 它的左、右子树也分别为二叉搜索树。

---

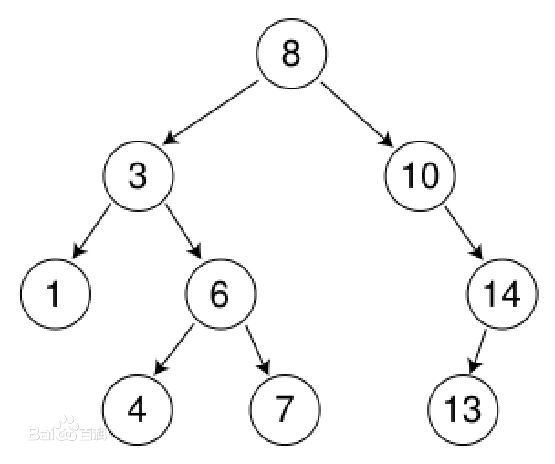
验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

1. 节点的左子树只包含小于当前节点的数。
2. 节点的右子树只包含大于当前节点的数。
3. 所有左子树和右子树自身必须也是二叉搜索树。

示例 :

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

解题思路

乍一看，这是一道很简单的题。只需要遍历整棵树，检查 node.right.val > node.val 和

node.left.val < node.val 对每个结点是否成立。

问题是，这种方法并不总是正确。不仅右子结点要大于该节点，整个右子树的元素都应该大于该节点。例如:这意味着我们需要在遍历树的同时保留结点的上界与下界，在比较时不仅比较子结点的值，也要与上下界比较。

上述思路可以用递归法实现:

• 首先将结点的值与上界和下界（如果有）比较。然后，对左子树和右子树递归进行该过程。

视频

视频讲解和源码-验证二叉搜索树

public boolean isValidBST(TreeNode root) {
    return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}

private boolean isValidBST(TreeNode root, long min, long max){
    if (root == null) {
        return true;
    }

    if (root.val <= min || root.val >= max){
        return false;
    }

    return isValidBST(root.left, min, root.val) && isValidBST(root.right, root.val, max);
}

---

二叉搜索树中第K小的元素

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：

你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 :

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 3

解题思路

1. 增加 getCount 方法来获取传入节点的子节点数（包括自己）
2. 从 root 节点开始判断k值和子节点数的大小决定递归路径是往左还是往右。

public int kthSmallest(TreeNode root, int k) {
    if (root == null) {
        return 0;
    }

    int leftCount = getCount(root.left);
    if (leftCount >= k) {
        return kthSmallest(root.left, k);
    } else if (leftCount + 1 == k) {
        return root.val;
    } else {
    	//注（1）
        return kthSmallest(root.right, k - leftCount - 1);
    }
}

private int getCount(TreeNode root) {
    if (root == null) {
        return 0;
    }

    return getCount(root.left) + getCount(root.right) + 1;
}

注：

（1）为什么是 k - leftCount - 1 而不是 k ，我们可以把当前的二叉树看成左右两部分。在执行到这个条件的时候，很明显，左边 leftCount 个数，加上根节点，都小于所要求的元素。接着，现在要从右子树搜索，很明显，搜索是往下的，不可能往上（原根节点的方向）搜索，故，之前 leftCount + 1 个数作废，所以所传入 k - leftCount - 1

---

数组 / 双指针

所谓双指针

指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个相同方向或者相反方向的指针进行扫描，从而达到相应的目的。

换言之，双指针法充分使用了数组有序这一特征，从而在某些情况下能够简化一些运算。

加一

给定一个非负数，表示一个数字数组，在该数的基础上+1，返回一个新的数组。该数字按照数位高低进行排列，最高位的数在列表的最前面。

示例 :

输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

解题思路

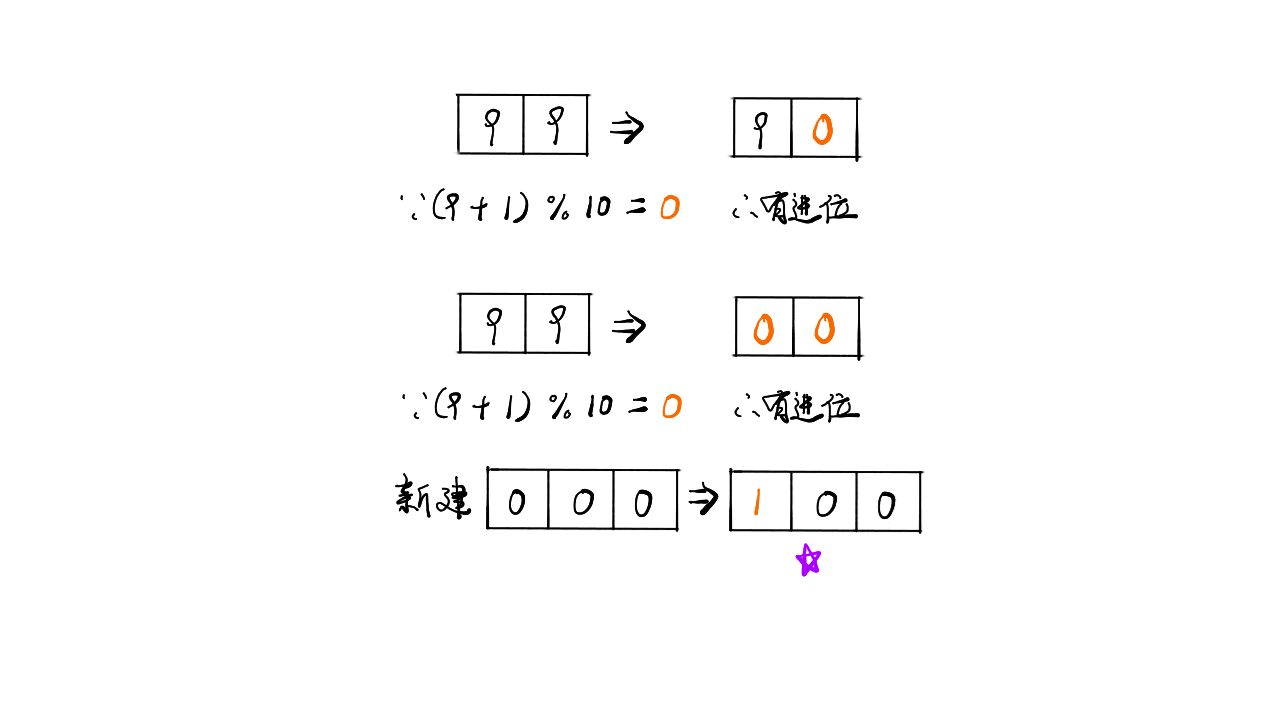
只需要判断有没有进位并模拟出它的进位方式，如十位数加 11 个位数置为 00，如此循环直到判断没有再进位就退出循环返回结果。

然后还有一些特殊情况就是当出现 9999、999999 之类的数字时，循环到最后也需要进位，出现这种情况时需要手动将它进一位。

视频

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一

    public int[] plusOne(int[] digits) {
        for (int i = digits.length - 1; i >= 0; i--) {
            digits[i]++;
            digits[i] = digits[i] % 10;
            if (digits[i] != 0) return digits;
        }
        digits = new int[digits.length + 1];
        digits[0] = 1;
        return digits;
    }

---

删除元素

给定一个数组和一个值，在原地删除与值相同的数字，返回新数组的长度。

解题思路

1. 定义一个 index 用于记录新数组下标，遍历数组
2. 如果与传入值不同，则其应存在于新数组中 index++ 并存入
3. 如果与传入值相同，说明重复，则直接跳过该数
4. 最后返回 index 即可

public int removeElement(int[] A, int elem) {
    if (A == null || A.length == 0) {
        return 0;
    }

    int index = 0;
    for (int i = 0; i < A.length; i++) {
        if (A[i] != elem) {
            A[index++] = A[i];
        }
    }

    return index;
}

---

删除排序数组中的重复数字

在原数组中“删除”重复出现的数字，使得每个元素只出现一次，并且返回“新”数组的长度。

示例 :

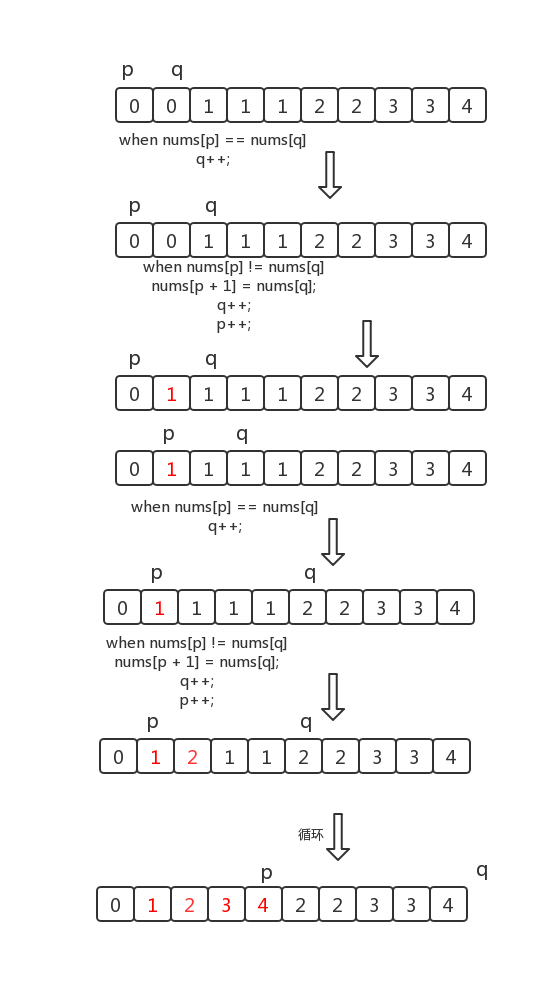
给定 nums = [0,0,1,1,1,2,2,3,3,4],

函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。

你不需要考虑数组中超出新长度后面的元素。

解题步骤

1. 数组完成排序后，我们可以放置两个指针 size 和 i，其中 size 是慢指针，而 i 是快指针。
2. 只要 nums[size] = nums[i] ，我们就增加 i 以跳过重复项。
3. 当我们遇到 nums[i] =nums[size] 时，跳过重复项的运行已经结束
4. 因此我们必须把它（nums[i]）的值复制到 nums[size+1]。
5. 然后递增 i 接着我们将再次重复相同的过程，直到 size 到达数组的末尾为止。

public int removeDuplicates(int[] A) {
    if (A == null || A.length == 0) {
        return 0;
    }

    int size = 0;
    for (int i = 0; i < A.length; i++) {
        if (A[i] != A[size]) {
            A[++size] = A[i];
        }
    }
    // (1)
    return size + 1;
}

注：因为 size 为下标，所以返回长度要加一

---

我的日程安排表 I

实现MyCalendar类来存储活动。如果新添加的活动没有重复，则可以添加。类将有方法book(int start，int end)。这代表左闭右开的间隔[start，end)有了预定，范围内的实数x，都满足start <= x < end，返回true。 否则，返回false，并且事件不会添加到日历中。

示例 :

MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(15, 25); // returns false
MyCalendar.book(20, 30); // returns true
解释:
第一个日程安排可以添加到日历中.  第二个日程安排不能添加到日历中，因为时间 15 已经被第一个日程安排预定了。
第三个日程安排可以添加到日历中，因为第一个日程安排并不包含时间 20 。

解题步骤

1. TreeMap 是一个有序的key-value集合，它通过 红黑树 实现，继承于AbstractMap，所以它是一个Map，即一个key-value集合。
2. TreeMap可以查询小于等于某个值的最大的key，也可查询大于等于某个值的最小的key。
3. 元素的顺序可以改变，并且对新的数组不会有影响。

• floorKey(K key) 方法用于返回小于或等于给定的键的所有键中，的最大键，或null，如果不存在这样的键

• ceilingKey(K key) 方法用于返回大于或等于返回到给定的键中，的最小键，或null，如果不存在这样的键

class MyCalendar {
    TreeMap<Integer, Integer> calendar;

    MyCalendar() {
        calendar = new TreeMap();
    }

    public boolean book(int start, int end) {
        Integer previous = calendar.floorKey(start), next = calendar.ceilingKey(start);
        if ((previous == null || calendar.get(previous) <= start) && (next == null || end <= next)) {
            calendar.put(start, end);
            return true;
        }
        return false;
    }
}

---

合并两个有序数组

合并两个排序的整数数组A和B变成一个新的数组。可以假设A具有足够的空间去添加B中的元素。

说明:

初始化 A 和 B 的元素数量分别为 m 和 n。

你可以假设 A 有足够的空间（空间大小大于或等于 m + n）来保存 B 中的元素。

示例:

输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

解题思路

• 双指针 / 从后往前
• 这里的指针 p 用于追踪添加元素的位置。

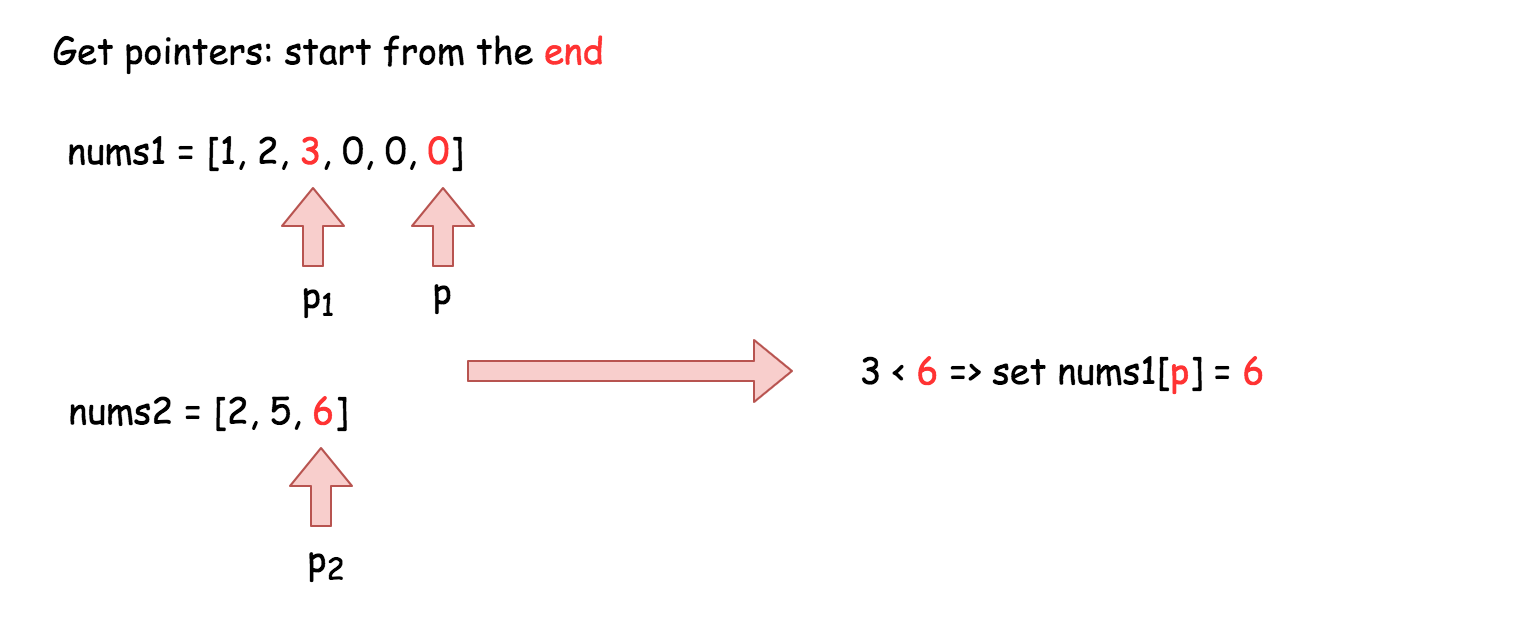
public void mergeSortedArray(int[] A, int m, int[] B, int n) {
    int i = m - 1, j = n - 1, index = m + n - 1;
    while (i >= 0 && j >= 0) {
        if (A[i] > B[j]) {
            A[index--] = A[i--];
        } else {
            A[index--] = B[j--];
        }
    }
    while (i >= 0) {
        A[index--] = A[i--];
    }
    while (j >= 0) {
        A[index--] = B[j--];
    }
}

---

贪心

顾名思义，贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

视频

贪心算法 - 2 理论基础

买卖股票的最佳时机

假设有一个数组，它的第i个元素是一支给定的股票在第i天的价格。如果你最多只允许完成一次交易(例如，一次买卖股票)，设计一个算法来找出最大利润。

注意:

• 你不能在买入股票前卖出股票。

示例 :

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要早于买入价格。

如果将测试范例 [7, 1, 5, 3, 6, 4]

绘制成图，我们发现：

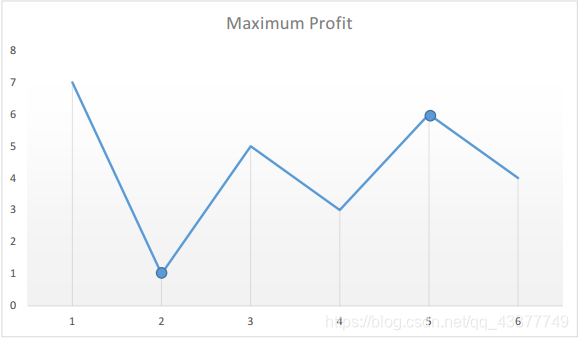
1. 我们需要找到最小的谷之后的最大的峰。
2. 我们可以维持两个变量 —— min 和 profit，它们分别对应迄今为止所得到的最小的谷值和最大的利润（卖出价格与最低价格之间的最大差值）。

public int maxProfit(int[] prices) {
    if (prices == null || prices.length == 0) {
        return 0;
    }

    int min = Integer.MAX_VALUE;  //记录最低的价格
    int profit = 0;
    for (int price : prices) {
        min = Math.min(price, min);
        profit = Math.max(price - min, profit);
    }

    return profit;
}

---

买卖股票的最佳时机 II

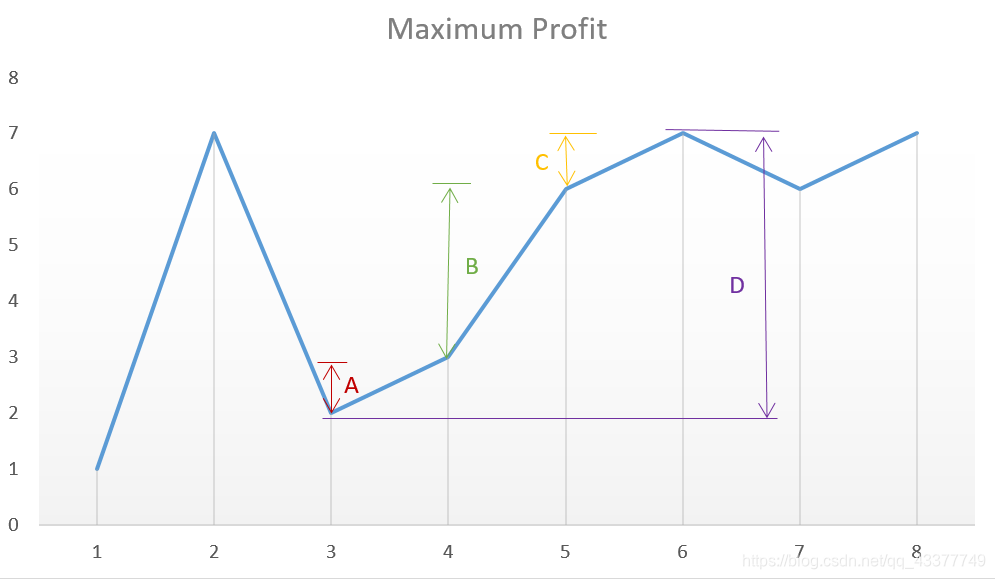
给定一个数组 prices 表示一支股票每天的价格。可以完成任意次数的交易, 不过不能同时参与多个交易，设计一个算法求出最大的利润。

解题思路

贪心：

1. 只要相邻的两天股票的价格是上升的,
2. 我们就进行一次交易, 获得一定利润。

视频

买卖股票的最佳时机 II by 代码会说话

    public int maxProfit(int[] prices) {
        int profit = 0;
        for(int i = 0 ; i < prices.length -1; i++) {
            if(prices[i + 1] > prices[i]) {
                profit += prices[i + 1] - prices[i];
            }
        }
        return profit;
    }

---

最大子数组

给定一个整数数组，找到一个具有最大和的子数组，返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

解题思路

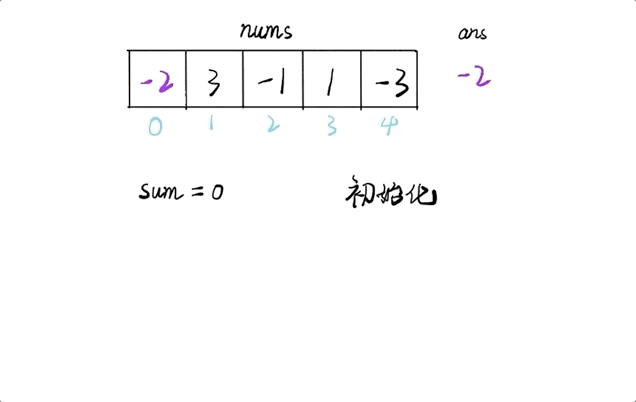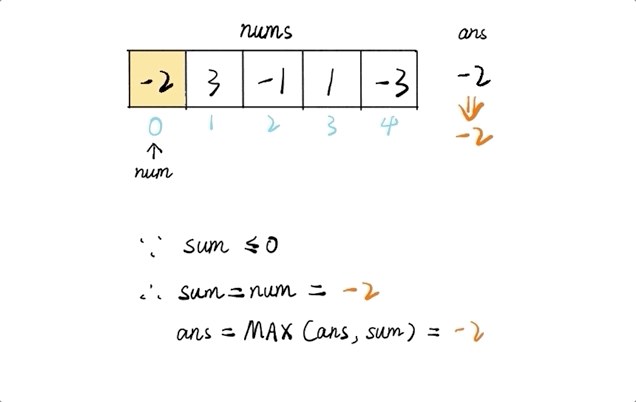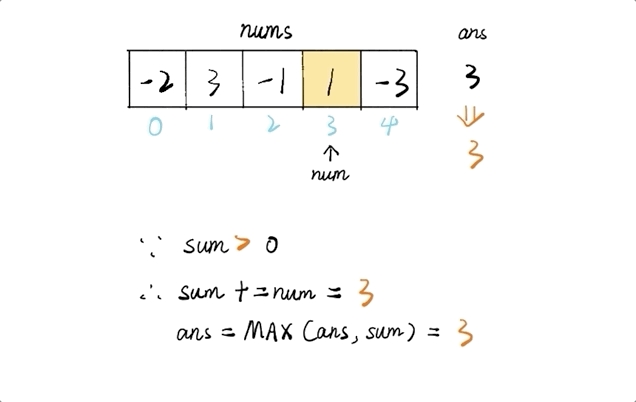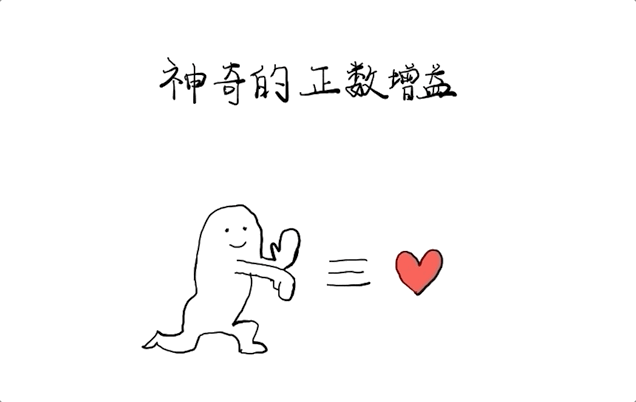
    public int maxSubArray(int[] nums) {
        if(nums == null || nums.length == 0) {
            return 0;
        }
        int max = Integer.MIN_VALUE;
        int sum = 0;
        for (int num : nums) {
            sum += num;
            max = Math.max(sum, max);
            sum = Math.max(sum, 0);
        }
        return max;
    }

---

主元素

给定一个整型数组，找出主元素，它在数组中的出现次数严格大于数组元素个数的二分之一(可以假设数组非空，且数组中总是存在主元素)。

解题思路

1. 重点在于：主元素数量大于数组所有元素的二分之一
2. 所以我们要做的是，选出一个出现次数大于其他所有数，出现次数和的数即可
3. 设一个计数器 currentMajor 候选数 和 一个 count 用于记录次数
4. 每当当前数和 currentMajor 值相同时， count 值 +1
5. 每当当前数和 currentMajor 值不同时， count 值 -1
6. 每次 count 等于 0 时，说明在之前访问的数组里 currentMajor 的数量小于或等于一半
7. 则将 currentMajor 赋值为当前数，继续寻找。

public int majorityNumber(List<Integer> nums) {
    int currentMajor = 0;
    int count = 0;

    for(Integer num : nums) {
        if(count == 0) {
            currentMajor = num;
        }

        if(num == currentMajor) {
            count++;
        } else {
            count--;
        }
    }
    return currentMajor;
}

---

Attention

• 为了提高文章质量，防止冗长乏味

下一部分算法题

• 本片文章篇幅总结越长。我一直觉得，一片过长的文章，就像一堂超长的 会议/课堂，体验很不好，所以我打算再开一篇文章

• 在后续文章中，我将继续针对链表 栈 队列 堆 动态规划 矩阵 位运算 等近百种，面试高频算法题，及其图文解析 + 教学视频 + 范例代码，进行深入剖析有兴趣可以继续关注 _yuanhao 的编程世界

• 不求快，只求优质，每篇文章将以 2 ～ 3 天的周期进行更新，力求保持高质量输出

相关文章

---

面试高频算法题汇总「图文解析 + 教学视频 + 范例代码」之 二分 + 哈希表 + 堆 + 优先队列 合集