ACM数论之旅13---容斥原理（一切都是命运石之门的选择(=ﾟωﾟ)ﾉ）

容斥原理我初中就听老师说过了，不知道你们有没有听过(/≧▽≦)/

百度百科说：

在计数时，必须注意没有重复，没有遗漏。

为了使重叠部分不被重复计算，人们研究出一种新的计数方法。

这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复。

这种计数的方法称为容斥原理。

好标准的说法（#－.－）

那我举个简单的例子

两个集合的容斥原理: 设A, B是两个有限集合

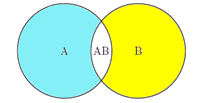
那么

|A + B| = |A| + |B| - |AB|

|A|表示A集合中的元素个数

三个集合的容斥原理: 设A, B, C是三个有限集合

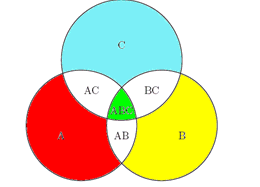
那么

|A + B + C| = |A| + |B| + |C| - |AB| - |AC| - |BC| + |ABC|

这就叫容斥原理

接下来直接做例题了

全错排（装错信封问题）

hdu 1465

http://acm.hdu.edu.cn/showproblem.php?pid=1465

n封信对应n个信封

求恰好全部装错了信封的方案数

本来全错排是有自己的一个公式的，叫全错排公式（跟容斥没关系）

那我顺便来讲讲全错排( ＞ω＜)

要装第i封信的时候，先把前i-1个信全装错信封，然后随便选其中一个与第i封信交换，有i-1种选法

那么dp[i] = (i-1) * dp[i-1]

但是还有一种情况

要装第i封信的时候，先从i-1封信中任选i-2个信把他们全装错信封，然后把剩下的那个信与第i个交换，从i-1封信中任选i-2个信有i-1种选法

那么dp[i] = (i-1) * dp[i-2]

两个式子联合起来

就是那么dp[i] = (i-1) * (dp[i-1] + dp[i-2])

这就是全错排公式，递推，递归都可以做

全错排递推AC代码：

 #include<cstdio>
 typedef long long LL;
 int n;
 LL dp[];
 void init(){
     dp[] = ;
     dp[] = ;
     for(int i = ; i <= ; i ++){
         dp[i] = (i-) * (dp[i-] + dp[i-]);
     }
 }
 int main(){
     init();
     while(~scanf("%d", &n)){
         printf("%I64d\n", dp[n]);
     }
 }

那么这题容斥怎么做呢？

首先，所有装信的总数是n!

（在n中任选一个信封放进一封信，然后在剩下的n-1中任选一个信封放进一封信，以此类推，所以是n*(n-1)*(n-2)... = n!）

假设

A1表示1封信装对信封，数量是(n-1)! （只有n-1个位置可以乱放）

A2表示2封信装对信封，数量是(n-2)! （只有n-2个位置可以乱放）

...

An表示n封信装对信封，数量是1

那么这题的答案就是

n! - C(n, 1)*|A1| + C(n, 2)*|A2| - C(n, 3)*|A3| + ... + (-1)^n * C(n, n)*|A4|

把C(n, m)用

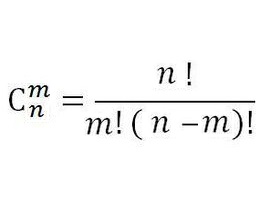代入式子

化简

n! - n! / 1! + n! / 2! - n! / 3! + ... + (-1)^n * n! / n!

提取n!

n!(1 - 1/1! + 1/2! - 1/3! + ... + (-1)^n * 1/n!)

附上容斥AC代码：

 #include<cstdio>
 typedef long long LL;
 int n, flag;
 LL fac[];
 LL ans;
 void init(){
     fac[] = ;
     for(int i = ; i <= ; i ++) fac[i] = fac[i-] * i;
 }
 int main(){
     init();
     while(~scanf("%d", &n)){
         ans = fac[n];
         flag = -;//容斥的符号变化
         for(int i = ; i <= n; i ++){
             ans += flag * fac[n] / fac[i];
             flag = -flag;
         }
         printf("%I64d\n", ans);
     }
 }

第二例题：

UVALive 7040

https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=5052

题意：给n盆花涂色，从m种颜色中选取k种颜色涂，保证正好用上k种颜色，你必须用上这k种颜色去涂满n个相邻的花，并且要求相邻花的颜色不同，求方案数。

(1 ≤ n, m ≤ 1e9 , 1 ≤ k ≤ 1e6 , k ≤ n, m)

首先，用k种颜色涂花，假如不考虑全部用上，那么总的方案数是多少

第一盆花有k种颜色选择，之后的花因为不能跟前一盆花的颜色相同，所以有k-1种选择

于是总方案数为k*(k-1)^(n-1)

因为题目问必须用上k种颜色

这里面包含了只用k-1种颜色的情况，应该减掉所有用k-1种的情况

减掉的东西里面，这里面包含了只用k-2种颜色的情况，应该加回来

...

反反复复，最后就得出答案了（这算是解释吗。。。）

最后答案就是

C(m,k) * ( k * (k-1)^(n-1) + [∑((-1)^i * C(k, k - i) * (k-i) * (k-i-1)^(n-1)) ] )    (1 <= i <= k-1)    红色表示容斥部分

（这里m有1e9，C(m, k)直接用for循环算，直接for循环从m*(m-1)*...*(m-k+1)再乘k的阶乘的逆元）

AC代码：

 #include<cstdio>
 typedef long long LL;
 const int N =  + ;
 const int MOD = (int)1e9 + ;
 int F[N], Finv[N], inv[N];
 LL pow_mod(LL a, LL b, LL p){
     LL ret = ;
     while(b){
         if(b & ) ret = (ret * a) % p;
         a = (a * a) % p;
         b >>= ;
     }
     return ret;
 }
 void init(){
     inv[] = ;
     for(int i = ; i < N; i ++){
         inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
     }
     F[] = Finv[] = ;
     for(int i = ; i < N; i ++){
         F[i] = F[i-] * 1ll * i % MOD;
         Finv[i] = Finv[i-] * 1ll * inv[i] % MOD;
     }
 }
 int comb(int n, int m){
     if(m <  || m > n) return ;
     return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
 }
 int main(){
     init();
     int T, n, m, k, ans, flag, temp;
     scanf("%d", &T);
     for(int cas = ; cas <= T; cas ++){
         scanf("%d%d%d", &n, &m, &k);
         ans = k * pow_mod(k-, n-, MOD) % MOD;
         flag = -;
         //计算容斥
         for(int i = ; i <= k-; i ++){
             ans = (ans + 1ll * flag * comb(k, k-i) * (k-i) % MOD * pow_mod((k-i-), n-, MOD) % MOD) % MOD;
             flag = -flag;
         }
         //接下来计算C(m, k)
         temp = Finv[k];
         for(int i = ; i <= k; i ++){
             temp = 1ll * temp * (m-k+i) % MOD;
         }
         ans = ((1ll * ans * temp) % MOD + MOD) % MOD;
         printf("Case #%d: %d\n", cas, ans);
     }
 }

第三例题：（容斥这章的例题我可能会写很多(o^∇^o)ﾉ预祝玩的开心have fun）

hdu 4135

http://acm.hdu.edu.cn/showproblem.php?pid=4135

题意：就是让你求(a,b)区间与n互质的数的个数.

我们可以先求(1~b)区间的答案，然后减去(1~a-1)区间的答案

这样问题就转换为(1~m)区间与n互质的数的个数

互质的不好求，我们可以求不互质的个数，然后减一下

所有我们先求出n的所有质因数，然后用容斥做

AC代码：

 #include<cstdio>
 #include<vector>
 using namespace std;
 typedef long long LL;
 vector <LL > prime_factor;
 vector <LL > vec;
 void init(LL x){
     //预处理质因子
     prime_factor.clear();
     for(LL i = ; i*i <= x; i++){
         if(x % i == ){
             prime_factor.push_back(i);
             while(x % i == ) x /= i;
         }
     }
     if(x > ) prime_factor.push_back(x);
     //预处理容斥中的倍数项，符号正好是一个减一个加
     int vec_size;
     vec.clear();
     for(int i = ; i < prime_factor.size(); i ++){
         vec_size = vec.size();//因为vec.size()在接下来的运算中会改变
         for(int j = ; j < vec_size; j ++){
             vec.push_back(vec[j] * prime_factor[i]);
         }
         vec.push_back(prime_factor[i]);
     }
 }
 LL work(LL x){
     //接下来容斥
     LL ans = x, flag = -;
     for(int i = ; i < vec.size(); i ++){
         ans += flag * x / vec[i];
         flag = -flag;
     }
     return ans;
 }
 int main(){
     int T;
     LL l, r, n;
     scanf("%d", &T);
     for(int cas = ; cas <= T; cas ++){
         scanf("%I64d%I64d%I64d", &l, &r, &n);
         init(n);
         printf("Case #%d: %I64d\n", cas, work(r) - work(l-));
     }
 }

容斥中的那些倍数我是这么处理的

比如30 = 2 * 3 * 5

一开始数组里面什么都没有

然后变成

2

然后把3挨个乘过去的值放在数组后面，同时将自己也放进数组

2 6 3

然后5也是一样

2 6 3 10 30 15 5

最后答案n就是等于

n - n / 2 + n / 6 - n / 3 + n / 10 - n / 30 + n / 15 - n / 5

当然，除了数组形式，还可以用位运算来实现容斥

AC代码：

 #include<cstdio>
 #include<vector>
 using namespace std;
 typedef long long LL;
 vector <LL > prime_factor;
 void init(LL x){
     //预处理质因子
     prime_factor.clear();
     for(LL i = ; i*i <= x; i++){
         if(x % i == ){
             prime_factor.push_back(i);
             while(x % i == ) x /= i;
         }
     }
     if(x > ) prime_factor.push_back(x);
 }
 LL work(LL x){
     //接下来容斥
     LL ans = x, cnt, temp;
     for(int i = ; i < ( << prime_factor.size()); i ++){
         cnt = ;
         temp = ;
         for(int j = ; j < prime_factor.size(); j ++){
             if(i & ( << j)){
                 temp *= prime_factor[j];
                 cnt ++;
             }
         }
         if(cnt & ) ans -= x / temp;
         else ans += x / temp;
     }
     return ans;
 }
 int main(){
     int T;
     LL l, r, n;
     scanf("%d", &T);
     for(int cas = ; cas <= T; cas ++){
         scanf("%I64d%I64d%I64d", &l, &r, &n);
         init(n);
         printf("Case #%d: %I64d\n", cas, work(r) - work(l-));
     }
 }

第四例题：

hdu 1695

http://acm.hdu.edu.cn/showproblem.php?pid=1695

题意:给你5个数a，b，c，d，k

在a~b中选一个x, c~d中选一个y，满足gcd(x,y) = k , 求(x,y) 的对数

a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000

在题目描述的最后一行有一句话，多组里面所有的a和c都是1（这题目不是坑爹吗(╯‵□′)╯︵┻━┻那输入a和c有什么用）

然后题目变成

在1~b中选一个x, 1~d中选一个y，满足gcd(x,y) = k , 求(x,y) 的对数 。。。（无语中。。。）

gcd(x, y) == k 说明x,y都能被k整除, 但是能被k整除的未必gcd=k  , 必须还要满足互质关系

那么问题就转化为

求1~b/k 和 1~d/k间，gcd(x,y) = 1对数的问题

假设b/k小于d/k

那么当y <= b/k时，就是求1到b/k的欧拉函数的和

y > b/k时，只好枚举y从b/k到d/k，用第3例题的求法

这样问题就解决了（注意：k可以等于0，要特判）

AC代码：

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 using namespace std;
 typedef long long LL;
 const int N = 1e5+ ;
 vector <LL > prime_factor;
 int phi[N], prime[N];
 int tot;//tot计数，表示prime[N]中有多少质数
 void Euler(){
     phi[] = ;
     for(int i = ; i < N; i ++){
         if(!phi[i]){
             phi[i] = i-;
             prime[tot ++] = i;
         }
         for(int j = ; j < tot && 1ll*i*prime[j] < N; j ++){
             if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-);
             else{
                 phi[i * prime[j] ] = phi[i] * prime[j];
                 break;
             }
         }
     }
 }
 void getFactors(int x){
     prime_factor.clear();
     for(int i = ; prime[i] <= x / prime[i]; i ++){
         if(x % prime[i] == ){
             prime_factor.push_back(prime[i]);
             while(x % prime[i] == ) x /= prime[i];
         }
     }
     if(x > ) prime_factor.push_back(x);
 }
 LL work(int n, int m){
     LL ans = n, cnt, temp;
     getFactors(m);
     for(int i = ; i < ( << prime_factor.size()); i ++){
         cnt = ;
         temp = ;
         for(int j = ; j < prime_factor.size(); j ++){
             if(i & ( << j)){
                 temp *= prime_factor[j];
                 cnt ++;
             }
         }
         if(cnt & ) ans -= n / temp;
         else ans += n / temp;
     }
     return ans;
 }
 int main(){
     Euler();
     int T, a, b, c, d, k;
     LL ans;
     scanf("%d", &T);
     for(int cas = ; cas <= T; cas ++){
         scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
         if(k == ){
             printf("Case %d: 0\n", cas);
             continue;
         }
         if(b > d) swap(b, d);//假设b<=d
         b /= k; d /= k;
         ans = ;
         for(int i = ; i <= b; i ++) ans += phi[i];
         for(int i = b + ; i <= d; i ++) ans += work(b, i);
         printf("Case %d: %I64d\n", cas, ans);
     }
 }

这题时间只能算卡过去的，因为正常计算下来，这样的代码会超时，只是数据水

这题正确的做法应该是莫比乌斯反演，我们以后会讲到

容来容去，脑子都乱了。。。。

＞﹏＜