Codeforces Good Bye 2018

咕bye 2018，因为我这场又咕咕咕了

无谓地感慨一句：时间过得真快啊(有毒

A.New Year and the Christmas Ornament

分类讨论后等差数列求和

又在凑字数了

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int a,b,c;
 int main()
 {
     scanf("%d%d%d",&a,&b,&c);
     printf("%d",min(min((a+)*,b*),(c-)*));
     return ;
 }

B.New Year and the Treasure Geolocation

坐标分别加起来除个$n$，没了

凑字数++

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 long long n,a,b,t1,t2;
 int main()
 {
     scanf("%lld",&n);
     for(int i=;i<=n;i++) scanf("%lld%lld",&t1,&t2),a+=t1,b+=t2;
     for(int i=;i<=n;i++) scanf("%lld%lld",&t1,&t2),a+=t1,b+=t2;
     printf("%lld %lld",a/n,b/n);
     return ;
 }

C.New Year and the Sphere Transmission

分解因数后变成了等差数列求和

凑字数停不下来了？

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N=;
 int n,cnt,facs[N];
 long long ans[N];
 int gcd(int a,int b)
 {
     return b?gcd(b,a%b):a;
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i*i<=n;i++)
         if(n%i==)
         {
             facs[++cnt]=i;
             if(i*i!=n)
                 facs[++cnt]=n/i;
         }
     for(int i=;i<=cnt;i++)
     {
         int g=gcd(facs[i],n),tot=n/g;
         ans[i]=1ll*(n-g+)*tot/;
     }
     sort(ans+,ans++cnt);
     for(int i=;i<=cnt;i++)
         printf("%lld ",ans[i]);
     return ;
 }

D.New Year and the Permutation Concatenation

不错的题 终于不在凑字数了

考虑容斥，计算不合法的方案数，这里我们要讲一讲如何实现next_permutation，是这样的：

以 1 3 5 4 2 为例

1.从序列末尾向前扫，直到一个位置pos序列开始下降 1 3 5 4 2

2.从后面这段递减的序列里找到第一个大于*pos的数，将pos位置的数与它交换 1 4 5 3 2

3.排序— —即翻转后面这段原来递减的序列 1 4 2 3 5

这样我们发现后面原来长度为n-pos的这段递减的序列被破坏了，而它原来是可以跟后面的一个排列配对的

那么显然对每个长度$len$统计有长度为$len$的递减序列的排列去掉即可(除了一种情况— —len==n，这时候没有排列能和它配对)

这样一来对每个$len$前$n-len$个可以随便排，后面$len$个又有$C_n^{len}$种选法，所以总方案数就是$\sum\limits_{len=1}^{n-1}\frac{n!}{len!}$，然后从总数里把这个容斥掉即可

 #include<cstdio>
 const int N=,mod=;
 int n,x,y,ans,fac[N],inv[N];
 void exGCD(int &x,int &y,int a,int b)
 {
     if(!b) x=,y=;
     else exGCD(y,x,b,a%b),y-=a/b*x;
 }
 int Inv(int nm,int md)
 {
     exGCD(x,y,nm,md);
     return (x%md+md)%md;
 }
 int main()
 {
     scanf("%d",&n),fac[]=inv[]=;
     for(int i=;i<=n;i++) fac[i]=1ll*fac[i-]*i%mod;
     inv[n]=Inv(fac[n],mod),ans=1ll*n*fac[n]%mod;
     for(int i=n-;i;i--) inv[i]=1ll*inv[i+]*(i+)%mod;
     for(int i=;i<=n-;i++) ans-=1ll*fac[n]*inv[i]%mod,ans=(ans+mod)%mod;
     printf("%d",ans);
     return ;
 }

E.New Year and the Acquaintance Estimation

观察样例/仔细分析/动手推理可以发现答案是一段隔2连续的区间！(我是第一种

所以只要求上下界就好了，怎么求呢？二分

怎么想到二分的呢？没想到，但是题目贴心地给了一个wiki的链接，里面有这样一个东西

这个定理可以在图的度数降序排好序的情况下检查图是否可行，这明摆着是告诉我们二分啊=。=

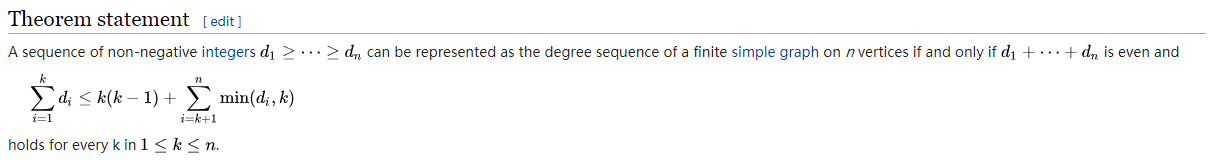
我们发现这个式子别的都好说，就是这个

$\sum\limits_{i=k+1}^{n}min(d_i,k)$

很麻烦啊，好像需要什么主席树/multiset？

并不需要，边扫边维护还未出现过的度数小于当前的$k$的点数的和sum即可，说白了就是前缀和，然后每次用$n-i-sum$更新。为什么？因为这就是后面那个式子里$k$的的贡献的增加量(未出现过的大于等于$k$的数)

注意二分+检查之后偏移的方向

 #include<cstdio>
 #include<vector>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N=;
 int mem[N],tmp[N],bkt[N];
 int n,l,r,rd,ld,hd,sum,odd;
 bool cmp(int a,int b)
 {
     return a>b;
 }
 int check(int x)
 {
     int p=,pos=;
     memset(bkt,,sizeof bkt);
     for(int i=;i<=n;i++)
     {
         if(mem[i]<x&&p<i)
             pos=++p,tmp[pos]=x;
         tmp[++p]=mem[i];
     }
     if(!pos) pos=++p,tmp[pos]=x;
     for(int i=;i<=p;i++) bkt[tmp[i]]++;
     long long lsum=,rsum=,fsum=;
     for(int i=;i<=p;i++)
     {
         lsum+=tmp[i],bkt[tmp[i]]--;
         rsum+=*(i-),rsum-=min(tmp[i],i-);
         fsum+=bkt[i-],rsum+=n-i+-fsum;
         if(lsum>rsum) return i>=pos?:-;
     }
     return ;
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
         scanf("%d",&mem[i]),sum+=mem[i];
     odd=sum%,sort(mem+,mem++n,cmp);
     l=,r=(n-odd)/,ld=rd=-;
     while(l<=r)
     {
         int mid=(l+r)/;
         if(check(*mid+odd)<) l=mid+;
         else ld=mid,r=mid-;
     }
     l=ld,r=(n-odd)/;
     while(l<=r)
     {
         int mid=(l+r)/;
         if(check(*mid+odd)>) r=mid-;
         else rd=mid,l=mid+;
     }
     if(ld==-||rd==-) printf("-1");
     else for(int i=ld;i<=rd;i++) printf("%d ",*i+odd);
     return ;
 }

F.New Year and the Mallard Expedition

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N=;
 char mapp[N]; long long len[N];
 long long n,wat,spa,ans,sta;
 int main()
 {
     scanf("%lld",&n);
     for(int i=;i<=n;i++)
         scanf("%lld",&len[i]);
     scanf("%s",mapp+);
     for(int i=;i<=n;i++)
     {
         if(mapp[i]=='G')
         {
             ans+=len[i]*;
             spa+=len[i]*;
             sta+=len[i];
         }
         else if(mapp[i]=='W')
         {
             wat=true;
             ans+=len[i]*;
             sta+=len[i];
         }
         else if(mapp[i]=='L')
         {
             if(sta<len[i])
             {
                 ans+=(wat?:)*(len[i]-sta);
                 sta=len[i];
             }
             ans+=len[i];
             sta-=len[i];
         }
         spa=min(spa,sta);
     }
     if(sta)    ans-=sta+spa;//ans-=(5-1)*spa/2,ans-=(3-1)*(sta-spa)/2;
     printf("%lld",ans);
     return ;
 }

首先模拟，草地先走路，水里游泳，岩浆飞过去。在这个过程中我们记录一下是否遇到了水，因为如果遇到岩浆飞不过去的情况，需要在之间走来走去/游来游去积攒体力。模拟的同时记录一个“可以用飞行代替行走”的路程的消耗，这个东西步步和你的耐力取min，最后如果它小于耐力就把它代表的行走换成飞行，如果还剩下一些就把一些游泳也换成飞行