最邻近规则分类KNN算法

例子：

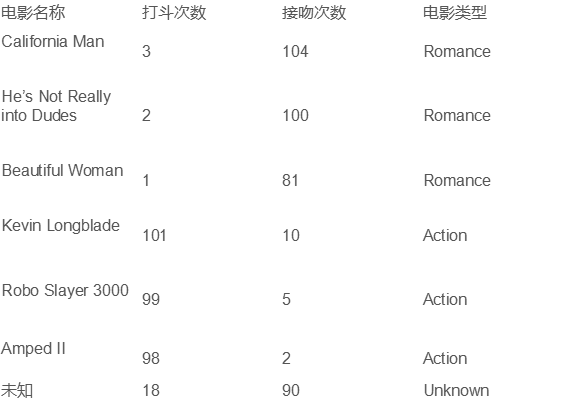
求未知电影属于什么类型：

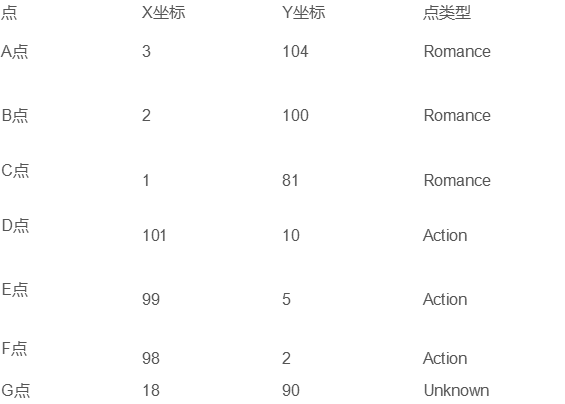
算法介绍：

步骤：

　 为了判断未知实例的类别，以所有已知类别的实例作为参照
选择参数K
计算未知实例与所有已知实例的距离
选择最近K个已知实例
根据少数服从多数的投票法则(majority-voting)，让未知实例归类为K个最邻近样本中最多数的类别

细节：

关于K的选择
关于距离的衡量方法：

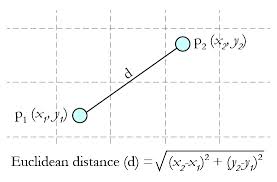
其他距离衡量：余弦值（cos）, 相关度（correlation）, 曼哈顿距离（Manhattan distance）

算法优点:

　　简单。
易于理解。
容易实现。
通过对K的选择可具备丢噪音数据的健壮性。

算法缺点：

　　需要大量空间储存所有已知实例。
算法复杂度高（需要比较所有已知实例与要分类的实例）。
当其样本分布不平衡时，比如其中一类样本过大（实例数量过多）占主导的时候，新的未知实例容易被归类为这个主导样本，因为这类样本实例的数量过大，但这个新的未知实例实际并木接近目标样本。

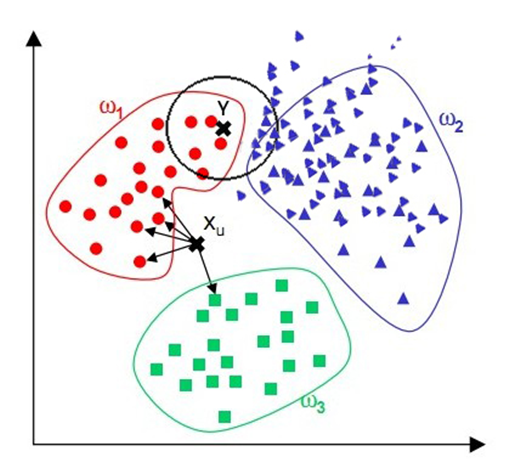
KNN代码（Python实现）：

 import csv

 import random

 import math

 import operator

 def loadDataset(filename, split, trainingSet=[], testSet=[]):

     with open(filename, 'r') as csvfile:

         lines = csv.reader(csvfile)

         dataset = list(lines) #得到文件中的数据

         for x in range(len(dataset) - 1):

             for y in range(4):

                 dataset[x][y] = float(dataset[x][y])

             if random.random() < split:   #以split为界限把数据集分为两部分

                 trainingSet.append(dataset[x])

             else:

                 testSet.append(dataset[x])

 def euclideanDistance(instance1, instance2, length):  #计算距离(传入两个实例和维度)

     distance = 0

     for x in range(length):

         distance += pow((instance1[x] - instance2[x]), 2)   #计算所有维度的平方和

     return math.sqrt(distance)

 def getNeighbors(trainingSet, testInstance, k):   #返回最近的几个邻域

     distances = [] #所有计算得出的距离的容器

     length = len(testInstance) - 1  #测试实例的维度

     for x in range(len(trainingSet)):

         dist = euclideanDistance(testInstance, trainingSet[x], length)

         distances.append((trainingSet[x], dist))

     distances.sort(key=operator.itemgetter(1)) #key=operator.itemgetter(1)根据第一个值域进行排序

     #print(distances)

     neighbors = []

     for x in range(k):

         neighbors.append(distances[x][0])

     return neighbors

 def getResponse(neighbors):

     classVotes = {}

     for x in range(len(neighbors)):

         response = neighbors[x][-1]

         if response in classVotes:

             classVotes[response] += 1

         else:

             classVotes[response] = 1

     sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)

     return sortedVotes[0][0]

 def getAccuracy(testSet, predictions):  #计算正确度

     correct = 0

     for x in range(len(testSet)):

         if testSet[x][-1] == predictions[x]:

             correct += 1

     return (correct / float(len(testSet))) * 100.0

 def main():

     # prepare data

     trainingSet = []

     testSet = []

     split = 0.67 #以split为界限把数据集分为两部分

     loadDataset(r'iris.data.txt', split, trainingSet, testSet)

     print('Train set: ' + repr(len(trainingSet)))

     print('Test set: ' + repr(len(testSet)))

     # generate predictions

     predictions = []

     k = 3

     for x in range(len(testSet)):

         neighbors = getNeighbors(trainingSet, testSet[x], k)

         result = getResponse(neighbors)

         predictions.append(result)

         print('> predicted=' + repr(result) + ', actual=' + repr(testSet[x][-1]))

     accuracy = getAccuracy(testSet, predictions)

     print('Accuracy: ' + repr(accuracy) + '%')

 if __name__ == '__main__':

     main()

虹膜数据：

5.1,3.5,1.4,0.2,Iris-setosa

4.9,3.0,1.4,0.2,Iris-setosa

4.7,3.2,1.3,0.2,Iris-setosa

4.6,3.1,1.5,0.2,Iris-setosa

5.0,3.6,1.4,0.2,Iris-setosa

5.4,3.9,1.7,0.4,Iris-setosa

4.6,3.4,1.4,0.3,Iris-setosa

5.0,3.4,1.5,0.2,Iris-setosa

4.4,2.9,1.4,0.2,Iris-setosa

4.9,3.1,1.5,0.1,Iris-setosa

5.4,3.7,1.5,0.2,Iris-setosa

4.8,3.4,1.6,0.2,Iris-setosa

4.8,3.0,1.4,0.1,Iris-setosa

4.3,3.0,1.1,0.1,Iris-setosa

5.8,4.0,1.2,0.2,Iris-setosa

5.7,4.4,1.5,0.4,Iris-setosa

5.4,3.9,1.3,0.4,Iris-setosa

5.1,3.5,1.4,0.3,Iris-setosa

5.7,3.8,1.7,0.3,Iris-setosa

5.1,3.8,1.5,0.3,Iris-setosa

5.4,3.4,1.7,0.2,Iris-setosa

5.1,3.7,1.5,0.4,Iris-setosa

4.6,3.6,1.0,0.2,Iris-setosa

5.1,3.3,1.7,0.5,Iris-setosa

4.8,3.4,1.9,0.2,Iris-setosa

5.0,3.0,1.6,0.2,Iris-setosa

5.0,3.4,1.6,0.4,Iris-setosa

5.2,3.5,1.5,0.2,Iris-setosa

5.2,3.4,1.4,0.2,Iris-setosa

4.7,3.2,1.6,0.2,Iris-setosa

4.8,3.1,1.6,0.2,Iris-setosa

5.4,3.4,1.5,0.4,Iris-setosa

5.2,4.1,1.5,0.1,Iris-setosa

5.5,4.2,1.4,0.2,Iris-setosa

4.9,3.1,1.5,0.2,Iris-setosa

5.0,3.2,1.2,0.2,Iris-setosa

5.5,3.5,1.3,0.2,Iris-setosa

4.9,3.6,1.4,0.1,Iris-setosa

4.4,3.0,1.3,0.2,Iris-setosa

5.1,3.4,1.5,0.2,Iris-setosa

5.0,3.5,1.3,0.3,Iris-setosa

4.5,2.3,1.3,0.3,Iris-setosa

4.4,3.2,1.3,0.2,Iris-setosa

5.0,3.5,1.6,0.6,Iris-setosa

5.1,3.8,1.9,0.4,Iris-setosa

4.8,3.0,1.4,0.3,Iris-setosa

5.1,3.8,1.6,0.2,Iris-setosa

4.6,3.2,1.4,0.2,Iris-setosa

5.3,3.7,1.5,0.2,Iris-setosa

5.0,3.3,1.4,0.2,Iris-setosa

7.0,3.2,4.7,1.4,Iris-versicolor

6.4,3.2,4.5,1.5,Iris-versicolor

6.9,3.1,4.9,1.5,Iris-versicolor

5.5,2.3,4.0,1.3,Iris-versicolor

6.5,2.8,4.6,1.5,Iris-versicolor

5.7,2.8,4.5,1.3,Iris-versicolor

6.3,3.3,4.7,1.6,Iris-versicolor

4.9,2.4,3.3,1.0,Iris-versicolor

6.6,2.9,4.6,1.3,Iris-versicolor

5.2,2.7,3.9,1.4,Iris-versicolor

5.0,2.0,3.5,1.0,Iris-versicolor

5.9,3.0,4.2,1.5,Iris-versicolor

6.0,2.2,4.0,1.0,Iris-versicolor

6.1,2.9,4.7,1.4,Iris-versicolor

5.6,2.9,3.6,1.3,Iris-versicolor

6.7,3.1,4.4,1.4,Iris-versicolor

5.6,3.0,4.5,1.5,Iris-versicolor

5.8,2.7,4.1,1.0,Iris-versicolor

6.2,2.2,4.5,1.5,Iris-versicolor

5.6,2.5,3.9,1.1,Iris-versicolor

5.9,3.2,4.8,1.8,Iris-versicolor

6.1,2.8,4.0,1.3,Iris-versicolor

6.3,2.5,4.9,1.5,Iris-versicolor

6.1,2.8,4.7,1.2,Iris-versicolor

6.4,2.9,4.3,1.3,Iris-versicolor

6.6,3.0,4.4,1.4,Iris-versicolor

6.8,2.8,4.8,1.4,Iris-versicolor

6.7,3.0,5.0,1.7,Iris-versicolor

6.0,2.9,4.5,1.5,Iris-versicolor

5.7,2.6,3.5,1.0,Iris-versicolor

5.5,2.4,3.8,1.1,Iris-versicolor

5.5,2.4,3.7,1.0,Iris-versicolor

5.8,2.7,3.9,1.2,Iris-versicolor

6.0,2.7,5.1,1.6,Iris-versicolor

5.4,3.0,4.5,1.5,Iris-versicolor

6.0,3.4,4.5,1.6,Iris-versicolor

6.7,3.1,4.7,1.5,Iris-versicolor

6.3,2.3,4.4,1.3,Iris-versicolor

5.6,3.0,4.1,1.3,Iris-versicolor

5.5,2.5,4.0,1.3,Iris-versicolor

5.5,2.6,4.4,1.2,Iris-versicolor

6.1,3.0,4.6,1.4,Iris-versicolor

5.8,2.6,4.0,1.2,Iris-versicolor

5.0,2.3,3.3,1.0,Iris-versicolor

5.6,2.7,4.2,1.3,Iris-versicolor

5.7,3.0,4.2,1.2,Iris-versicolor

5.7,2.9,4.2,1.3,Iris-versicolor

6.2,2.9,4.3,1.3,Iris-versicolor

5.1,2.5,3.0,1.1,Iris-versicolor

5.7,2.8,4.1,1.3,Iris-versicolor

6.3,3.3,6.0,2.5,Iris-virginica

5.8,2.7,5.1,1.9,Iris-virginica

7.1,3.0,5.9,2.1,Iris-virginica

6.3,2.9,5.6,1.8,Iris-virginica

6.5,3.0,5.8,2.2,Iris-virginica

7.6,3.0,6.6,2.1,Iris-virginica

4.9,2.5,4.5,1.7,Iris-virginica

7.3,2.9,6.3,1.8,Iris-virginica

6.7,2.5,5.8,1.8,Iris-virginica

7.2,3.6,6.1,2.5,Iris-virginica

6.5,3.2,5.1,2.0,Iris-virginica

6.4,2.7,5.3,1.9,Iris-virginica

6.8,3.0,5.5,2.1,Iris-virginica

5.7,2.5,5.0,2.0,Iris-virginica

5.8,2.8,5.1,2.4,Iris-virginica

6.4,3.2,5.3,2.3,Iris-virginica

6.5,3.0,5.5,1.8,Iris-virginica

7.7,3.8,6.7,2.2,Iris-virginica

7.7,2.6,6.9,2.3,Iris-virginica

6.0,2.2,5.0,1.5,Iris-virginica

6.9,3.2,5.7,2.3,Iris-virginica

5.6,2.8,4.9,2.0,Iris-virginica

7.7,2.8,6.7,2.0,Iris-virginica

6.3,2.7,4.9,1.8,Iris-virginica

6.7,3.3,5.7,2.1,Iris-virginica

7.2,3.2,6.0,1.8,Iris-virginica

6.2,2.8,4.8,1.8,Iris-virginica

6.1,3.0,4.9,1.8,Iris-virginica

6.4,2.8,5.6,2.1,Iris-virginica

7.2,3.0,5.8,1.6,Iris-virginica

7.4,2.8,6.1,1.9,Iris-virginica

7.9,3.8,6.4,2.0,Iris-virginica

6.4,2.8,5.6,2.2,Iris-virginica

6.3,2.8,5.1,1.5,Iris-virginica

6.1,2.6,5.6,1.4,Iris-virginica

7.7,3.0,6.1,2.3,Iris-virginica

6.3,3.4,5.6,2.4,Iris-virginica

6.4,3.1,5.5,1.8,Iris-virginica

6.0,3.0,4.8,1.8,Iris-virginica

6.9,3.1,5.4,2.1,Iris-virginica

6.7,3.1,5.6,2.4,Iris-virginica

6.9,3.1,5.1,2.3,Iris-virginica

5.8,2.7,5.1,1.9,Iris-virginica

6.8,3.2,5.9,2.3,Iris-virginica

6.7,3.3,5.7,2.5,Iris-virginica

6.7,3.0,5.2,2.3,Iris-virginica

6.3,2.5,5.0,1.9,Iris-virginica

6.5,3.0,5.2,2.0,Iris-virginica

6.2,3.4,5.4,2.3,Iris-virginica

5.9,3.0,5.1,1.8,Iris-virginica

最邻近规则分类KNN算法的更多相关文章

机器学习--最邻近规则分类KNN算法
理论学习: 3. 算法详述 3.1 步骤: 为了判断未知实例的类别,以所有已知类别的实例作为参照选择参数K 计算未知实例与所有已知实例的距离选 ...
机器学习算法 - 最近邻规则分类KNN
上节介绍了机器学习的决策树算法,它属于分类算法,本节我们介绍机器学习的另外一种分类算法:最近邻规则分类KNN,书名为k-近邻算法. 它的工作原理是:将预测的目标数据分别跟样本进行比较,得到一组距离的数 ...
kNN(K-Nearest Neighbor)最邻近规则分类
KNN最邻近规则,主要应用领域是对未知事物的识别,即推断未知事物属于哪一类,推断思想是,基于欧几里得定理,推断未知事物的特征和哪一类已知事物的的特征最接近: K近期邻(k-Nearest Neighb ...
kNN(K-Nearest Neighbor)最邻近规则分类（转）
KNN最邻近规则,主要应用领域是对未知事物的识别,即判断未知事物属于哪一类,判断思想是,基于欧几里得定理,判断未知事物的特征和哪一类已知事物的的特征最接近: K最近邻(k-Nearest Neighb ...
最邻近规则分类(K-Nearest Neighbor)KNN算法
自写代码: # Author Chenglong Qian from numpy import * #科学计算模块 import operator #运算符模块 def createDaraSet( ...
4.2 最邻近规则分类(K-Nearest Neighbor)KNN算法应用
1 数据集介绍: 虹膜 150个实例萼片长度,萼片宽度,花瓣长度,花瓣宽度 (sepal length, sepal width, petal length and petal wi ...
python实现简单分类knn算法
原理:计算当前点(无label,一般为测试集)和其他每个点(有label,一般为训练集)的距离并升序排序,选取k个最小距离的点,根据这k个点对应的类别进行投票,票数最多的类别的即为该点所对应的类别.代 ...
机器学习KNN算法
KNN(最邻近规则分类K-Nearest-Neighibor)KNN算法 1. 综述 1.1 Cover和Hart在1968年提出了最初的邻近算法 1.2 分类(classific ...

随机推荐

a标签--超链接
一.链接到其他网站 <body> <a href="https://www.baidu.com" target="_blank">百度& ...
my-innodb-heavy-4G.cnf配置文件注解
[client] ####客户端 port = 3306 ####mysql客户端连接时的默认端口号 socket = /application/mysql-5.5.32/tmp/mysql.sock ...
Kubernetes 1.5 配置dashboard
配置kubernetes的dashboard相对简单.同样的,只需要从源码中获取到dashboard-controller.yaml及dashboard-service.yaml文件,稍加修改即可: ...
P1022 计算器的改良
P1022 计算器的改良题目背景 NCL 是一家专门从事计算器改良与升级的实验室,最近该实验室收到了某公司所委托的一个任务:需要在该公司某型号的计算器上加上解一元一次方程的功能.实验室将这个任务交给 ...
Git和Github入门
推文:官方手册,十分详细推文:git和github快速入门一.git使用 1.git安装 (1)windows 网站:https://git-scm.com/download/win下载安装即可 ...
如何在Mongodb中实现数据超时自动删除功能？
在工作过程中,我们难免会遇到这样的问题,我们想保存一些数据,但是我们对这些数据的要求并不高,有时候往往只是想要某个时间范围内的数据,比如我们如果永远只关心从当前时间往前推半年内的数据特性,那么我们就不 ...
Typora 自定义主题修改左右间距
打开偏好设置,打开主题文件夹比如要修改night主题中的间距,编辑night.css文件,修改#write样式即可. 修改其他样式类试.
bzoj千题计划172：bzoj1192: [HNOI2006]鬼谷子的钱袋
http://www.lydsy.com/JudgeOnline/problem.php?id=1192 1,2,4,8,…… n-2^k 可以表示n以内的任意数若n-2^k 和之前的数相等,一个 ...
jdk源码
Java 8 之默认方法(Default Methods) public interface Player { String getName(); default boolean isMale() { ...
[整理]内存重叠之memcpy、memmove
函数原型: void *memcpy( void *dest, const void *src, size_t count ); void *memmove( void* dest, const vo ...

最邻近规则分类KNN算法

最邻近规则分类KNN算法的更多相关文章

随机推荐

热门专题