Viterbi algorithm

HMM（隐马尔可夫模型）是用来描述隐含未知参数的统计模型，是一个关于时序的概率模型，它描述了一个由隐藏的马尔可夫链生成状态序列，再由状态序列生成观测序列的过程。其中，状态之间的转换以及观测序列和状态序列之间都存在一定的概率关系。

任何一个HMM都可以通过下列五元组来描述：

:param obs:观测序列

:param states:隐状态

:param start_p:初始概率（隐状态）

:param trans_p:转移概率（隐状态）

:param emit_p: 发射概率 （隐状态表现为显状态的概率）

而Viterbi算法是解决隐马第三问题（求观察序列的最可能标注序列）。 
算法通过已知的可以观察到的序列，和一些已知的状态转换之间的概率情况，通过综合状态之间的转移概率和前一个状态的情况计算出概率最大的状态转换路径，从而推断出隐含状态的序列的情况。

维基百科动态图表示Viterbi算法过程

---

一个简单问题

问题描述

隐含的身体状态 = { 健康 , 发烧 }

可观察的感觉状态 = { 正常 , 冷 , 头晕 }

月儿预判的阿驴身体状态的概率分布 = { 健康：0.6 , 发烧： 0.4 }

月儿认为的阿驴身体健康状态的转换概率分布 = {健康->健康： 0.7 ,健康->发烧： 0.3 ,发烧->健康：0.4 ,发烧->发烧： 0.6}

月儿认为的在相应健康状况条件下，阿驴的感觉的概率分布 = {健康，正常：0.5 ，冷 ：0.4 ，头晕： 0.1 ；发烧，正常：0.1 ，冷 ：0.3 ，头晕： 0.6 }

阿驴连续三天的身体感觉依次是： 正常、冷、头晕 。

利用五元组来描述问题

 states = ('Health', 'Fever')
 observations = ('normal', 'cold', 'dizzy')
 start_probability = {'Health': 0.6, 'Fever': 0.4}
 transition_probability = {
         'Health' : {'Health': 0.7, 'Fever': 0.3},
         'Fever' : {'Health': 0.4, 'Fever': 0.6},
         }
 emission_probability = {
         'Health' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
         'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
         }

代码实现Viterbi 算法

 import numpy
 def Viterbi () :
     #已知条件
     states = ('Health', 'Fever')
     observations = ('normal', 'cold', 'dizzy')
     start_probability = {'Health': 0.6, 'Fever': 0.4}
     transition_probability = {
         'Health' : {'Health': 0.7, 'Fever': 0.3},
         'Fever' : {'Health': 0.4, 'Fever': 0.6},
         }
     emission_probability = {
         'Health' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
         'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
     }
     day = 3
     s = len(states)
     V = []      

     Wether = []
     Temp = []
     #求解初始状态可能
     for j in list(range(s)):
         Temp.append(start_probability.get(states[j]) * emission_probability.get(states[j])[observations[0]])
     V.append(Temp)
     #根据初始状态求解
     Wether.append(states[V[0].index(max(V[0]))]);

     #求解第2 - day 状态转换概率
     prob = []
     for d in [i + 1 for i in list(range( day - 1))]:
         prob = []
         pp = -1
         for j in list(range(s)):
             Temp = []
             for k in list(range(s)):
                 np = V[d-1][j] * transition_probability.get(states[j])[states[k]] * emission_probability.get(states[k])[observations[d]]
                 Temp.append(np)
                 #记录路径
                 if np > pp:
                     m1 = j
                     m2 = k
                     pp = np
             prob.append(Temp)

         print('Compute_Probability:')
         print(prob)
         Wether.append(states[m2])
         V.append(prob[m1])
         print('Large_One:')
         print(prob[m1])

     print(V)
     print(Wether)

 if __name__ == '__main__':
     Viterbi()

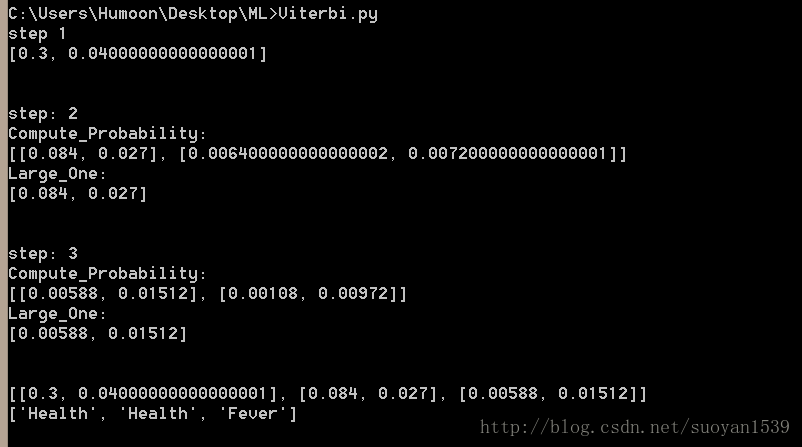
结果截图