C++ 生成洛伦兹的蝴蝶
这里使用 C++ 计算轨迹,生成 Python 文件,使用 matplotlib 绘图。
// simulator.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
// #include "pch.h" //预编译头,自行添加相关头文件 struct vec
{
double x;
double y;
double z;
}; vec operator*(vec v, double n)
{
return { v.x * n , v.y * n , v.z * n};
} vec operator+(vec &x, vec &y)
{
return {x.x + y.x, x.y + y.y, x.z + y.z};
} //参数
double a = ;
double b = ;
double c = ; vec velocity(vec &pos)
{
vec velocity;
velocity.x = a * (pos.y - pos.x);
velocity.y = pos.x * (b - pos.z) - pos.y;
velocity.z = pos.x * pos.y - c * pos.z; return velocity;
} //时间微元
double dt = 0.001; int main()
{
std::vector<vec> state; //初始条件
vec init_state = { 5.0, 5.0 , 5.0}; vec p = init_state; int ii = ;
for (int i = ; i < ii; ++i)
{
vec v = velocity(p);
vec dp = v * dt;
p = p + dp;
state.push_back(p);
printf("\r[%2.1lf%%|%5d] p -> (%lf,%lf,%lf)", (double)i / ii * , i, p.x, p.y, p.z);
} printf("\n\nsaving..."); //输出python文件 std::ostringstream ox;
std::ostringstream oy;
std::ostringstream oz; ox << "[";
oy << "[";
oz << "["; for (size_t i = ; i < state.size(); ++i)
{
ox << state[i].x;
oy << state[i].y;
oz << state[i].z; ox << ",";
oy << ",";
oz << ","; if ((i + ) % == )
{
ox << std::endl;
oy << std::endl;
oz << std::endl;
}
} ox << "]";
oy << "]";
oz << "]"; std::ofstream f;
f.open("output.py"); f << "import numpy as np" << std::endl;
f << "import matplotlib.pyplot as plt" << std::endl;
f << "from mpl_toolkits.mplot3d import Axes3D" << std::endl; f << "x = " << ox.str();
f << std::endl;
f << "y = " << oy.str();
f << std::endl;
f << "z = " << oz.str();
f << std::endl; f << "X = np.array(x)" << std::endl;
f << "Y = np.array(y)" << std::endl;
f << "Z = np.array(z)" << std::endl; f << std::endl; // f << "" << std::endl;
f << "fig = plt.figure()" << std::endl;
f << "ax = Axes3D(fig)" << std::endl;
f << "ax.plot(X, Y, Z)" << std::endl;
f << "plt.show()" << std::endl;
f << "" << std::endl; f.close();
}
然后会输出 output.py
依赖的包有:numpy, matplotlib
然后直接执行 >python output.py即可
结果:
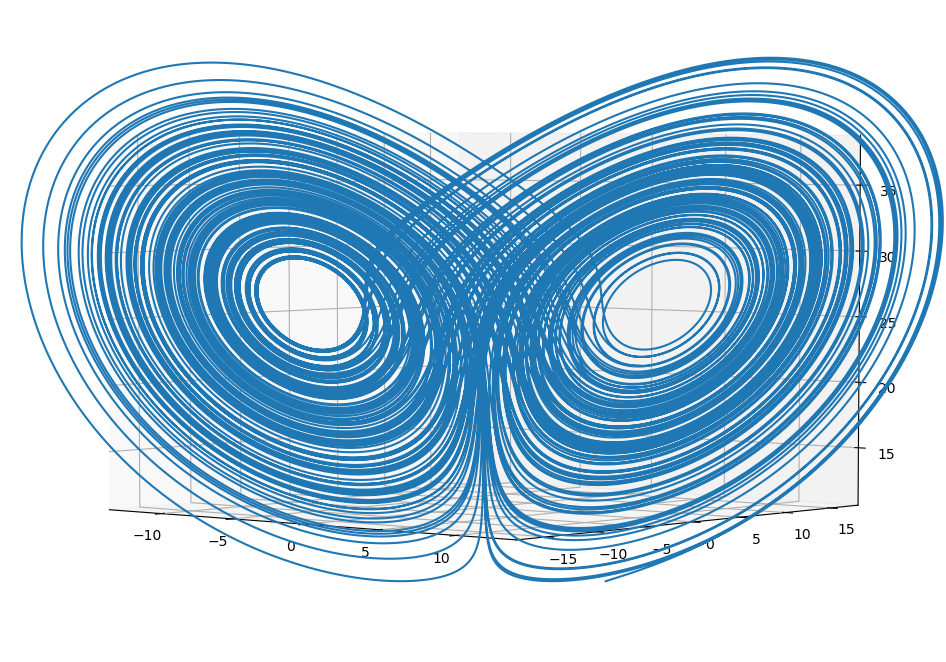
C++ 生成洛伦兹的蝴蝶的更多相关文章
- 洛伦兹曲线(Lorenz curve)提升指数、提升表和提升图
sklearn实战-乳腺癌细胞数据挖掘 https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campai ...
- 基尼系数(Gini coefficient),洛伦茨系数
20世纪初意大利经济学家基尼,于1922年提出的定量测定收入分配差异程度的指标.它是根据洛伦茨曲线找出了判断分配平等程度的指标(如下图). 设实际收入分配曲线和收入分配绝对平等曲线之间的面积为A,实际 ...
- 混沌理论(Chaos theory)和非线性系统
混沌理论(Chaos theory)是关于非线性系统在一定参数条件下展现分岔(bifurcation).周期运动与非周期运动相互纠缠,以至于通向某种非周期有序运动的理论.在耗散系统和保守系统中,混沌运 ...
- 用R做逻辑回归之汽车贷款违约模型
数据说明 本数据是一份汽车贷款违约数据 application_id 申请者ID account_number 账户号 bad_ind 是否违约 vehicle_year ...
- Windows phone应用开发[19]-RSA数据加密
在这个系列的第十六章节中Windows phone应用开发[16]-数据加密 中曾详细讲解过windows phone 常用的MD5,HMAC_MD5,DES,TripleDES[3DES] 数据加密 ...
- snort-2.9.7.0源码安装过程
2015/02/15,centos6.5-64-minimal,初始205个包 [root@localhost snort]# yum install wget[root@localhost snor ...
- 信用评分卡Credit Scorecards (1-7)
欢迎关注博主主页,学习python视频资源,还有大量免费python经典文章 python风控评分卡建模和风控常识 https://study.163.com/course/introductio ...
- boost 随机数发生器
Random 随机数 在很多应用中都需要使用随机数.本库力求提供一个高效的,通用的随机数库.boost库有多种随机数生成方式.先熟悉一下各种随机数生成器的概念. 数字生成器(Number Ge ...
- 统计随机数及临界值Web Service接口
(2017-02-04 银河统计) 统计函数API概念 API(Application Programming Interface,应用程序编程接口)是一些预先定义的函数,目的是提供应用程序与开发 ...
随机推荐
- pre的内容自动转行
使pre的内容自动换行(转) <pre> 元素可定义预格式化的文本.被包围在 pre 元素中的文本通常会保留空格和换行符.而文本也会呈现为等宽字体. <pre> 标签的一个常见 ...
- Axure之动态面板:登录面板切换
无论是谁,在刚开始接触一门不太熟悉的东西时都有一种恐惧感,但是慢慢多练习几遍,再多琢磨琢磨,形成自己的见解和认识,就掌握的差不多了.我说的是题外话,现在转入正题. 面板切换,也就是我们通常所有的tab ...
- android studio 报红解决
/Users/houzhibin/gradle/wrapper/dists/gradle-4.1-all/bzyivzo6n839fup2jbap0tjew/gradle-4.1-all.zip
- gzy的摄影梦
好像当身高180的摄影师啊. 记录一下素材,等自己有相机了,就一一实现. 竟然有人在看哎. 一袭红衣的女子,将手伸出窗外,开心的看这漫天大雪. 今天的晚霞,近处是蓝色,颜色逐渐变淡,一直延伸到远处.( ...
- Apache的安装与配置
apahe官网 http://www.apache.org/ 安装及配置https://blog.csdn.net/liyang4534/article/details/78036591 常见问题的处 ...
- Python的优势及应用领域
Python的优势 Python是一门解释型语言,是比较容易入门. Python的程序代码更接近英语,更好好理解. Python的扩展库非常丰富. Python与C的粘合性非常好. Python的缺点 ...
- 第十二节:WebApi自动生成在线Api文档的两种方式
一. WebApi自带生成api文档 1. 说明 通过观察,发现WebApi项目中Area文件夹下有一个HelpPage文件夹,如下图,该文件夹就是WebApi自带的生成Api的方式,如果该文件夹没了 ...
- 最短路径(Dijkstra算法)
算法局限性:边的权值不能为负. 需要两个辅助数组dist[],path[],分别记录起点到各点的最短距离和最短路径 算法步骤: 1.根据起点v0初始化dist[]和path[]数组. 2.在剩下的点中 ...
- 提交变更(git commit)
当所有的变更都进入暂存区,就可以使用git commit进行提交了 $ git commit 执行这句话后,会弹出文本编辑区(自己配置的或默认的),文本编辑器可能会显示如下内容 # Please en ...
- HTML required
required required属性表明该控件为必填项.required特性可用于任何类型的输入元素.required属性是布尔类型属性,无需专门把它设置为true,只需将它添加到标签中即可.一个表 ...
