最大熵模型和EM算法

一、极大似然
已经发生的事件是独立重复事件，符合同一分布
已经发生的时间是可能性（似然）的事件
利用这两个假设，已经发生时间的联合密度值就最大，所以就可以求出总体分布f中参数θ

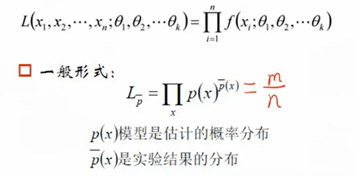
用极大似然进行机器学习
有监督学习：最大熵模型
无监督学习：GMM

二、熵和信息
自信息i(x) = -log(p(x)) 信息是对不确定性的度量。概率是对确定性的度量，概率越大，越确定，可能性越大。信息越大，越不确定。

熵是对平均不确定性的度量。熵是随机变量不确定性的度量，不确定性越大，熵值越大。
H(x) = -∑p(x)log⁡P(x)

互信息，其实我不不关心一个事件的大小，更关心的是知道某个信息之后，对于你关心的那个事件的不确定性的减少。互信息是对称的。
i(y, x) = i(y) – i(y|x) = log(p(y|x)/p(y))

平均互信息
决策树中的“信息增益”其实就是平均互信息I(x, y), 后面那部分就是互信息，前面p(x,y)相当于权重。这就与机器学习相关的点了。平均互信息=熵-条件熵

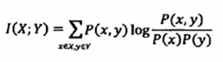
信息论与机器学习的关系

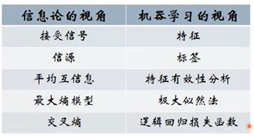
交叉熵

评价两个概率分布的差异性，比如一个概率分布是01分布，另一个概率分布也是01分布，但是他们分布的概率不一样，一个3/7，一个是6/4

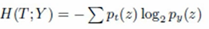
逻辑回归中的交叉熵代价函数，用来衡量误差，a是预测值，y是实际值

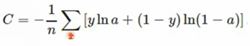
相对熵（KL散度） 也是衡量两个概率分布的差异性，可以理解成一种广泛的距离。不具有对称性。

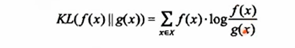
三、最大熵原理

（比较理想的模型，实际实现的时候计算量比较大，只适合于自然语言处理中的一小部分问题，在近两年大家提到的频率没有那么高了，因为deeplearning的兴起，很多用神经网络替换了。）

凡是已知的条件认为是一种约束，对于未知的条件，我们认为是均匀分布的且没有任何偏见。条件熵最大是一个自然的规律，它意味着我们所有的条件概率的分布在约束条件下也符合平均的。
承认已知事物，对未知事务不做任何假设，没有任何偏见，熵取最大的时候，是各个概率都相等的时候

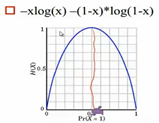
最大熵存在且唯一（凸优化）

最大熵原理进行机器学习
最大化条件熵得出的结果就是我们要得到的条件概率的分布P(y|x)，就是我们要求的模型
x表示特征，y表示标签

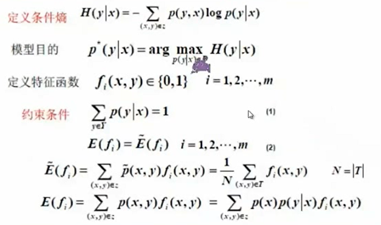
理解约束条件

若引入新知识，p(y4)=0.5

再次引入新知识，条件概率约束，怎么样得到无偏的最大熵模型。

用凸优化(求最小值)理论求解Maxent

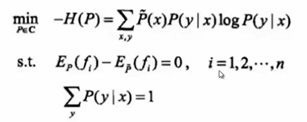
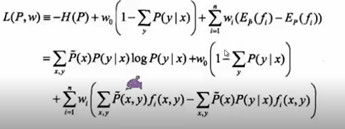
原始问题是求凸函数的最小值，对偶问题是求其对偶函数的最大值，在最大函数不是凸的情况下，原来问题的最小值会比对偶问题的最大值还大一点点，有一段gap，但对于凸函数来说gap会等于0，所有只要求对偶问题的最大值就够了，就能够求到原始问题最小值对应的值。题就相当于解完了。

泛函求导，由于P不是一个变量，是一个函数，所以涉及到泛函求导。

求偏导，得到条件概率，得到我们苦苦追寻的p(y|x)，其中的w是我们要求的。

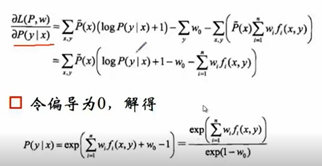
但是上面这个条件概率所有情况加起来是不等于1的，所以我们进行归一化，将值相加再除以它，下面就是最大熵模型的形式，一个非常简单的形式——指数函数。确定指数函数的参数就是训练的过程。最原始的训练方法是GIS，后面又提出IIS。下图还举了一个最大熵模型转换为Logistic回归的例子，对输入x和输出y去做一个f(x,y)的定义的时候，可以转化。

主要应用：自然语言处理中的词性标注、句法分析。最大熵的库:github上面minixalpha/Pycws 用最大熵完成抽取的特征

四、EM算法
EM算法在高斯模型里面的体现
EM算法求解GMM问题，下面是个无监督的问题。男女在身高上都符合高斯分布，是属于女生的分布多还是属于男生的分布多，哪个分布多点，就属于哪类。

上面那个例子就是，两个高斯分布，高斯分布男，高斯分布女，并分别对应概率π1,π2（相当于系数权重）

拟合出一套对数似然函数，括号里面是一个Xi出现的概率，权重相乘加和后就是结果

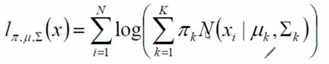
r(i,k)可以看成是其中一个高斯分布在生成数据xi时所作的贡献，先假定参数已知。

基于已经知道的值，做一个加和就能反过来求μ和西格玛和π，其中Nk是某一个高斯型对所有身高的人数的贡献，即对每个确定的组分对所有人求和，比如高斯分布女的概率求所有人加和，这个值应该就是所有女生的人数。

EM算法最原始的思路

凸函数 函数的期望大于等于期望的函数

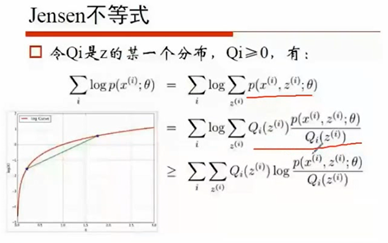
当Q等于下个这个值时，等号成立

求Q的过程就是求E（期望），然后再基于Q，求紧下界的最大值，从而求出θ。反复迭代得到

最终要求的是隐含变量Z，Q是为了方便求解Z引入的一个中间变量，Q是Z的某一个分布。Q通过jensen不等式和一系列的值，E步过程求得值。Z对应到我们上面高斯分布模型里面就是上面的π，Q是上面的r(i,k)。EM算法是一种框架，Z可以是你要求的任何变量。