基础概念【softmax|normalizatoin|standardization】

目录

一、softmax

二、normalization

三、standardization

一、softmax

为什么使用softmax,不用normalization?

“max” because amplifies probability of largest

“soft” because still assigns some probability to smaller

softmax层是一种归一化的方式，常应用在多分类的最后一阶段，对于网络产生的结果 x_i 执行 softmax(X)_i = exp(x_i) / ∑_jⁿ exp(x_j)

作用：

1、将原来的输入归一到[0,1]区间

2、使用exp的意义是 exp是单调递增函数且函数值为正数，这样可以保证根据输出大小得出概率，也是为了之后求导方便，exp的导数为exp

3、上溢和下溢问题

假设所有的x_i都等于某个常数c， 我们可以发现所有的输出都是 1/n。从数值上来说，当c的量级很大时，exp(c)就会出现上溢的问题，当c是很小的负数时，exp(c)就会下溢，这意味着softmax的分母会变成0,所以最后的结果是未定义的。

这两个问题能通过计算softmax(z)同时解决，其中 z = x - max_i x_i , 因为softmax解析上的函数值不会因为从输入向量减去或者加上标量而改变即softmax( X - c ) = softmax(X)，通过减去max_i x_i

导致exp的参数最大为0，这排除了上溢的可能，另外对于分母来说至少会有一项是1,这样避免了下溢

4、softmax求导

二、Normalization

1、含义： 将数据的值压缩到[0，1]区间，便于不同单位或者量级的指标能够进行比较和加权

2、好处：

1  提高迭代求解的收敛速度

归一化在梯度下降求解中的作用

在梯度下降中多数时候原始数据若没经过特征处理，数据的各个维度是存在着量级的差别，假如线性函数Ax+By+b=C，X维度数量级是十，Y的数量级是万，那么求出的A就比B大，那么在用梯度下降求解最优解过程中，对A求偏导每次变化是和X成线性的（结果只和x相关），对B求偏导是和B成线性的（结果只与y相关），这样就造成两个维度下降速度不一致的问题，在图像上面显示就是A每次走的step很小，B的step很大，可能导致某一个维度由于数量级较大已经到达最低点，而其他维度由于数量级的差异未到达最低点，先到达最低点的维度需要等待其他维度，走出的曲线是震荡性较大图像：
---------------------
作者：golden_xuhaifeng
来源：CSDN
原文：https://blog.csdn.net/golden_xuhaifeng/article/details/79742581
版权声明：本文为博主原创文章，转载请附上博文链接！

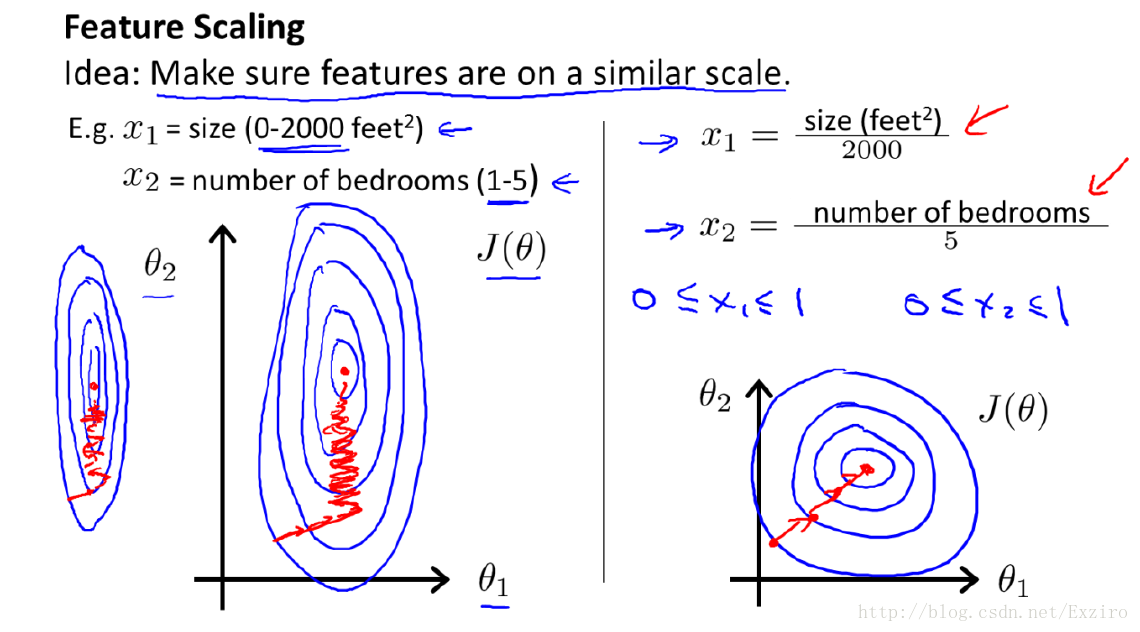
如左图所示，x1的取值范围大，所以θ₁ 只需经过少量几步就可以到达 极值点，但是由于x2的取值范围小，所以θ2要经过许多步才能到达极值点，经过归一化之后，如右图，θ₁和θ2

可以同时经过相同的步数到达极值点，因此归一化可以提高迭代收敛的速度。

2 提高迭代求解的精度

比如计算欧式距离：由于x1的取值范围 大于 x2的取值范围，因此最后x1对距离结果的影响要大于x2,这就会造成精精度的损失

3、归一化方法：

1、归一到【0，1】区间

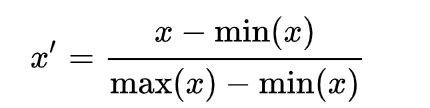
2、归一到【-1，1】

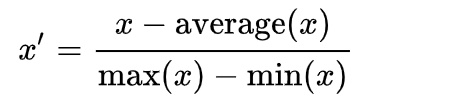
3、归一到【a，b】

（1）首先找到原本样本数据X的最小值Min及最大值Max
（2）计算系数：k=（b-a)/(Max-Min)
（3）得到归一化到[a,b]区间的数据：Y=a+k(X-Min)  或者 Y=b+k(X-Max)

三、Standardization

    对每个特征的数据值变成 均值为0，方差为1

好处：

1 使得不同度量之间的特征具有可比性，对目标函数的影响体现在几何分布上，而不是数值上

2 不改变数据原始分布

归一化和标准化区别：

归一化特点：使各个特征维度对目标函数的影响权重是一致的，即使得那些扁平分布的数据伸缩变换成类圆形。这也就改变了原始数据的一个分布。

标准化特点：通过一系列的平移压缩操作，不改变原始数据的分布

引于https://www.zhihu.com/question/20467170

从采用大单位的身高和体重这两个特征来看，如果采用标准化，不改变样本在这两个维度上的分布，则左图还是会保持二维分布的一个扁平性；而采用归一化则会在不同维度上对数据进行不同的伸缩变化（归一区间，会改变数据的原始距离，分布，信息），使得其呈类圆形。

虽然这样样本会失去原始的信息，但这防止了归一化前直接对原始数据进行梯度下降类似的优化算法时最终解被数值大的特征所主导。归一化之后，各个特征对目标函数的影响权重是一致的。这样的好处是在提高迭代求解的精度。