机器学习之决策树一-ID3原理与代码实现

决策树之系列一ID3原理与代码实现

本文系作者原创，转载请注明出处:https://www.cnblogs.com/further-further-further/p/9429257.html

应用实例：

你是否玩过二十个问题的游戏，游戏的规则很简单：参与游戏的一方在脑海里想某个事物，
其他参与者向他提问题，只允许提20个问题，问题的答案也只能用对或错回答。问问题的人通过
推断分解，逐步缩小待猜测事物的范围。决策树的工作原理与20个问题类似，用户输人一系列数
据，然后给出游戏的答案。如下表

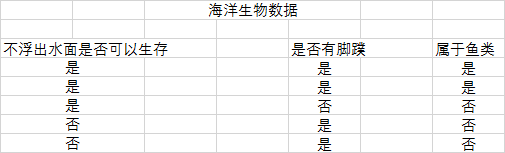
假如我告诉你，我有一个海洋生物，它不浮出水面可以生存，并且没有脚蹼，你来判断一下是否属于鱼类？

通过决策树，你就可以快速给出答案不是鱼类。

决策树的目的就是在一大堆无序的数据特征中找出有序的规则，并建立决策树（模型）。

决策树比较文绉绉的介绍

决策树学习是一种逼近离散值目标函数的方法。通过将一组数据中学习的函数表示为决策树，从而将大量数据有目的的分类，从而找到潜在有价值的信息。决策树分类通常分为两步---生成树和剪枝；

树的生成 --- 自上而下的递归分治法；

剪枝 --- 剪去那些可能增大错误预测率的分枝。

决策树的方法起源于概念学习系统CLS（Concept Learning System）, 然后发展最具有代表性的ID3（以信息熵作为目标评价函数）算法，最后又演化为C4.5, C5.0,CART可以处理连续属性。

这篇文章主要介绍ID3算法原理与代码实现（属于分类算法）

分类与回归的区别

回归问题和分类问题的本质一样，都是针对一个输入做出一个输出预测，其区别在于输出变量的类型。

分类问题是指，给定一个新的模式，根据训练集推断它所对应的类别（如：+1，-1），是一种定性输出，也叫离散变量预测；

回归问题是指，给定一个新的模式，根据训练集推断它所对应的输出值（实数）是多少，是一种定量输出，也叫连续变量预测。

举个例子：预测明天的气温是多少度，这是一个回归任务；预测明天是阴、晴还是雨，就是一个分类任务。

分类模型可将回归模型的输出离散化，回归模型也可将分类模型的输出连续化。

信息论相关知识

来自王小猴<<机器学习实战>>学习总结（二）------决策树算法(https://zhuanlan.zhihu.com/p/29980400)，他将原理说得很透彻形象，这里借鉴一下。

1. 信息熵

在决策树算法中，熵是一个非常非常重要的概念。

一件事发生的概率越小，我们说它所蕴含的信息量越大。

比如：我们听女人能怀孕不奇怪，如果某天听到哪个男人怀孕了，那这个信息量就很大了......。

所以我们这样衡量信息量：

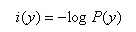
其中，P(y)是事件发生的概率。

信息熵就是所有可能发生的事件的信息量的期望：

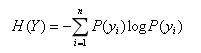
表达了Y事件发生的不确定度。

2. 条件熵

表示在X给定条件下，Y的条件概率分布的熵对X的数学期望。其数学推导如下：

 

                                   

条件熵H（Y|X）表示在已知随机变量X的条件下随机变量Y的不确定性。注意一下，条件熵中X也是一个变量，意思是在一个变量X的条件下（变量X的每个值都会取到），另一个变量Y的熵对X的期望。

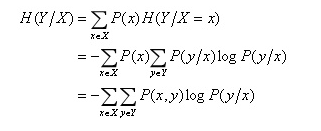
举个例子

例：女生决定主不主动追一个男生的标准有两个：颜值和身高，如下表所示：

上表中随机变量Y=｛追，不追｝，P(Y=追)=2/3，P(Y=不追)=1/3，得到Y的熵：

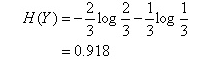
这里还有一个特征变量X,X=｛高，不高｝。当X=高时，追的个数为1，占1/2，不追的个数为1，占1/2，此时：

                           

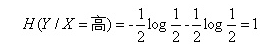
同理：

                               

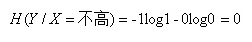
(注意：我们一般约定，当p=0时，plogp=0)

所以我们得到条件熵的计算公式：

 

3. 信息增益

当我们用另一个变量X对原变量Y分类后，原变量Y的不确定性就会减小了(即熵值减小)。而熵就是不确定性，不确定程度减少了多少其实就是信息增益。这就是信息增益的由来，所以信息增益定义如下：

                                

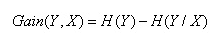
决策树算法

1. 算法简介

决策树算法是一类常见的分类和回归算法，顾名思义，决策树是基于树的结构来进行决策的。

以二分类为例，我们希望从给定训练集中学得一个模型来对新的样例进行分类。

以上面海洋生物为例

no surfacing：不浮出水面是否可以生存

flippers：是否有脚蹼

将表特征量化（是：1，否：0）

我们可以建立这样一颗决策树（后面结果证明，这是最佳的决策树）：

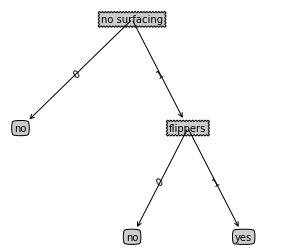
代码实现

paython3.6，Spyder运行环境，每行代码我基本都做了注释，最终能生成最优决策树结构，并用pyplot绘制了决策树，以及该决策树的叶子结点，树的深度。

ID3算法的核心是在决策树的各个结点上应用信息增益准则进行特征选择。具体做法是：

• 从根节点开始，对结点计算所有可能特征的信息增益，选择信息增益最大的特征作为结点的特征，并由该特征的不同取值构建子节点；
• 对子节点递归地调用以上方法，构建决策树；
• 直到所有特征的信息增益均很小或者没有特征可选时为止。

myTrees.py文件：

 # -*- coding: utf-8 -*-
 """
 Created on Thu Aug  2 17:09:34 2018
 决策树ID3的实现
 @author: weixw
 """
 from math import log
 import operator
 #原始数据
 def createDataSet():
     dataSet = [[1, 1, 'yes'],
                [1, 1, 'yes'],
                [1, 0, 'no'],
                [0, 1, 'no'],
                [0, 1, 'no']]
     labels = ['no surfacing','flippers']
     return dataSet, labels

 #多数表决器
 #列中相同值数量最多为结果
 def majorityCnt(classList):
     classCounts = {}
     for value in classList:
         if(value not in classCounts.keys()):
             classCounts[value] = 0
         classCounts[value] +=1
     sortedClassCount = sorted(classCounts.iteritems(),key = operator.itemgetter(1),reverse =True)
     return sortedClassCount[0][0]

 #划分数据集
 #dataSet:原始数据集
 #axis:进行分割的指定列索引
 #value:指定列中的值
 def splitDataSet(dataSet,axis,value):
     retDataSet= []
     for featDataVal in dataSet:
         if featDataVal[axis] == value:
             #下面两行去除某一项指定列的值，很巧妙有没有
             reducedFeatVal = featDataVal[:axis]
             reducedFeatVal.extend(featDataVal[axis+1:])
             retDataSet.append(reducedFeatVal)
     return retDataSet

 #计算香农熵
 def calcShannonEnt(dataSet):
     #数据集总项数
     numEntries = len(dataSet)
     #标签计数对象初始化
     labelCounts = {}
     for featDataVal in dataSet:
         #获取数据集每一项的最后一列的标签值
         currentLabel = featDataVal[-1]
         #如果当前标签不在标签存储对象里，则初始化，然后计数
         if currentLabel not in labelCounts.keys():
             labelCounts[currentLabel] = 0
         labelCounts[currentLabel] += 1
     #熵初始化
     shannonEnt = 0.0
     #遍历标签对象，求概率，计算熵
     for key in labelCounts.keys():
         prop = labelCounts[key]/float(numEntries)
         shannonEnt -= prop*log(prop,2)
     return shannonEnt

 #选出最优特征列索引
 def chooseBestFeatureToSplit(dataSet):
     #计算特征个数，dataSet最后一列是标签属性，不是特征量
     numFeatures = len(dataSet[0])-1
     #计算初始数据香农熵
     baseEntropy = calcShannonEnt(dataSet)
     #初始化信息增益，最优划分特征列索引
     bestInfoGain = 0.0
     bestFeatureIndex = -1
     for i in range(numFeatures):
         #获取每一列数据
         featList = [example[i] for example in dataSet]
         #将每一列数据去重
         uniqueVals = set(featList)
         newEntropy = 0.0
         for value in uniqueVals:
             subDataSet = splitDataSet(dataSet,i,value)
             #计算条件概率
             prob = len(subDataSet)/float(len(dataSet))
             #计算条件熵
             newEntropy +=prob*calcShannonEnt(subDataSet)
         #计算信息增益
         infoGain = baseEntropy - newEntropy
         if(infoGain > bestInfoGain):
             bestInfoGain = infoGain
             bestFeatureIndex = i
     return bestFeatureIndex

 #决策树创建
 def createTree(dataSet,labels):
     #获取标签属性，dataSet最后一列，区别于labels标签名称
     classList = [example[-1] for example in dataSet]
     #树极端终止条件判断
     #标签属性值全部相同，返回标签属性第一项值
     if classList.count(classList[0]) == len(classList):
         return classList[0]
     #只有一个特征（1列）
     if len(dataSet[0]) == 1:
         return majorityCnt(classList)
     #获取最优特征列索引
     bestFeatureIndex = chooseBestFeatureToSplit(dataSet)
     #获取最优索引对应的标签名称
     bestFeatureLabel = labels[bestFeatureIndex]
     #创建根节点
     myTree = {bestFeatureLabel:{}}
     #去除最优索引对应的标签名，使labels标签能正确遍历
     del(labels[bestFeatureIndex])
     #获取最优列
     bestFeature = [example[bestFeatureIndex] for example in dataSet]
     uniquesVals = set(bestFeature)
     for value in uniquesVals:
         #子标签名称集合
         subLabels = labels[:]
         #递归
         myTree[bestFeatureLabel][value] = createTree(splitDataSet(dataSet,bestFeatureIndex,value),subLabels)
     return myTree

 #获取分类结果
 #inputTree:决策树字典
 #featLabels:标签列表
 #testVec:测试向量  例如：简单实例下某一路径 [1,1]  => yes（树干值组合，从根结点到叶子节点）
 def classify(inputTree,featLabels,testVec):
     #获取根结点名称，将dict转化为list
     firstSide = list(inputTree.keys())
     #根结点名称String类型
     firstStr = firstSide[0]
     #获取根结点对应的子节点
     secondDict = inputTree[firstStr]
     #获取根结点名称在标签列表中对应的索引
     featIndex = featLabels.index(firstStr)
     #由索引获取向量表中的对应值
     key = testVec[featIndex]
     #获取树干向量后的对象
     valueOfFeat = secondDict[key]
     #判断是子结点还是叶子节点：子结点就回调分类函数，叶子结点就是分类结果
     #if type(valueOfFeat).__name__=='dict': 等价 if isinstance(valueOfFeat, dict):
     if isinstance(valueOfFeat, dict):
         classLabel = classify(valueOfFeat,featLabels,testVec)
     else:
         classLabel = valueOfFeat
     return classLabel

 #将决策树分类器存储在磁盘中，filename一般保存为txt格式
 def storeTree(inputTree,filename):
     import pickle
     fw = open(filename,'wb+')
     pickle.dump(inputTree,fw)
     fw.close()
 #将瓷盘中的对象加载出来，这里的filename就是上面函数中的txt文件
 def grabTree(filename):
     import pickle
     fr = open(filename,'rb')
     return pickle.load(fr)

最优决策树生成

treePlotter.py文件：

 '''
 Created on Oct 14, 2010

 @author: Peter Harrington
 '''
 import matplotlib.pyplot as plt

 decisionNode = dict(boxstyle="sawtooth", fc="0.8")
 leafNode = dict(boxstyle="round4", fc="0.8")
 arrow_args = dict(arrowstyle="<-")

 #获取树的叶子节点
 def getNumLeafs(myTree):
     numLeafs = 0
     #dict转化为list
     firstSides = list(myTree.keys())
     firstStr = firstSides[0]
     secondDict = myTree[firstStr]
     for key in secondDict.keys():
         #判断是否是叶子节点（通过类型判断，子类不存在，则类型为str；子类存在，则为dict）
         if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
             numLeafs += getNumLeafs(secondDict[key])
         else:   numLeafs +=1
     return numLeafs

 #获取树的层数
 def getTreeDepth(myTree):
     maxDepth = 0
     #dict转化为list
     firstSides = list(myTree.keys())
     firstStr = firstSides[0]
     secondDict = myTree[firstStr]
     for key in secondDict.keys():
         if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
             thisDepth = 1 + getTreeDepth(secondDict[key])
         else:   thisDepth = 1
         if thisDepth > maxDepth: maxDepth = thisDepth
     return maxDepth

 def plotNode(nodeTxt, centerPt, parentPt, nodeType):
     createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
              xytext=centerPt, textcoords='axes fraction',
              va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

 def plotMidText(cntrPt, parentPt, txtString):
     xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
     yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
     createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

 def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
     numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
     depth = getTreeDepth(myTree)
     firstSides = list(myTree.keys())
     firstStr = firstSides[0] #the text label for this node should be this
     cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
     plotMidText(cntrPt, parentPt, nodeTxt)
     plotNode(firstStr, cntrPt, parentPt, decisionNode)
     secondDict = myTree[firstStr]
     plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
     for key in secondDict.keys():
         if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
             plotTree(secondDict[key],cntrPt,str(key))        #recursion
         else:   #it's a leaf node print the leaf node
             plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
             plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
             plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
     plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
 #if you do get a dictonary you know it's a tree, and the first element will be another dict
 #绘制决策树
 def createPlot(inTree):
     fig = plt.figure(1, facecolor='white')
     fig.clf()
     axprops = dict(xticks=[], yticks=[])
     createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
     #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
     plotTree.totalW = float(getNumLeafs(inTree))
     plotTree.totalD = float(getTreeDepth(inTree))
     plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
     plotTree(inTree, (0.5,1.0), '')
     plt.show()

 #绘制树的根节点和叶子节点（根节点形状：长方形，叶子节点：椭圆形）
 #def createPlot():
 #    fig = plt.figure(1, facecolor='white')
 #    fig.clf()
 #    createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
 #    plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
 #    plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
 #    plt.show()

 def retrieveTree(i):
     listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
                   {'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
                   ]
     return listOfTrees[i]

 #thisTree = retrieveTree(0)
 #createPlot(thisTree)
 #createPlot()
 #myTree = retrieveTree(0)
 #numLeafs =getNumLeafs(myTree)
 #treeDepth =getTreeDepth(myTree)
 #print(u"叶子节点数目：%d"% numLeafs)
 #print(u"树深度：%d"%treeDepth)

决策树绘制

testTrees_3.py测试文件：

 # -*- coding: utf-8 -*-
 """
 Created on Fri Aug  3 19:52:10 2018

 @author: weixw
 """
 import myTrees as mt
 import treePlotter as tp
 #测试
 dataSet, labels = mt.createDataSet()
 #copy函数：新开辟一块内存，然后将list的所有值复制到新开辟的内存中
 labels1 = labels.copy()
 #createTree函数中将labels1的值改变了，所以在分类测试时不能用labels1
 myTree = mt.createTree(dataSet,labels1)
 #保存树到本地
 mt.storeTree(myTree,'myTree.txt')
 #在本地磁盘获取树
 myTree = mt.grabTree('myTree.txt')
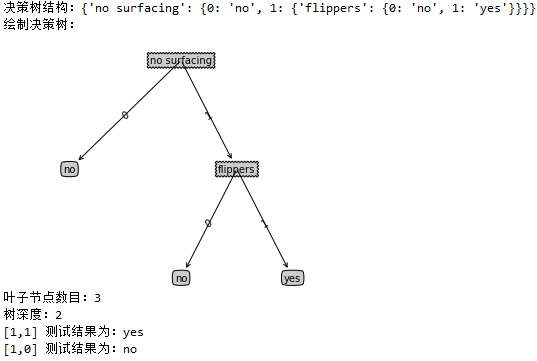
 print (u"决策树结构：%s"%myTree)
 #绘制决策树
 print(u"绘制决策树：")
 tp.createPlot(myTree)
 numLeafs =tp.getNumLeafs(myTree)
 treeDepth =tp.getTreeDepth(myTree)
 print(u"叶子节点数目：%d"% numLeafs)
 print(u"树深度：%d"%treeDepth)
 #测试分类 简单样本数据3列
 labelResult =mt.classify(myTree,labels,[1,1])
 print(u"[1,1] 测试结果为：%s"%labelResult)
 labelResult =mt.classify(myTree,labels,[1,0])
 print(u"[1,0] 测试结果为：%s"%labelResult)

测试代码

运行结果：

不要让懒惰占据你的大脑，不要让妥协拖垮你的人生。青春就是一张票，能不能赶上时代的快车，你的步伐掌握在你的脚下。