【做题】ECFinal2018 J - Philosophical … Balance——dp

原文链接 https://www.cnblogs.com/cly-none/p/ECFINAL2018J.html

题意：给出一个长度为\(n\)的字符串\(s\)，要求给\(s\)的每个后缀\(s[i:]\)分配权值\(k_i\)（实数），满足\(0 \leq k_i \leq 1\)，且\(\sum_i k_i = 1\)。再此基础上，最大化

\[\min_{i=1}^n \left( \sum_{j=1}^n k_j {\rm {lcp}} (s[i:],s[j:]) \right)
\]

\(n \leq 2 \times 10^5\)

第一步当然是构建SAM（反串），令\(s[i:]\)在parent树上对应的结点为\(p_i\)，\(dep_i\)为结点\(i\)所能表示的最长串，那么我们要最大化的就是\(\min_{i=1}^n \left( \sum_{j=1}^n k_j dep_{{\rm {lca}} (p_i,p_i)} \right)\)。

在这里树的结构恰好为权值的计算提供了一种类似分治的结构，因此我们考虑用树上dp解决这个问题。

于是我们令\(dp_i\)为仅考虑结点\(i\)的子树的答案。如果\(i\)是后缀结点，那么显然\(dp_i = dep_i\)。这样就确定了初始值。

然后就考虑合并。我们设结点\(u\)有孩子结点\(v\)。那么假设我们把\(k\)点权值分配到\(v\)的子树中，\(v\)能对答案产生的贡献就是\(dp_v k + dep_u (1-k) = (dp_v - dep_u)k + dep_u\)。我们所要做的就是对这些一次函数分配\(k\)，使\(k\)的总和为\(1\)，且它们的值取\(\min\)后尽可能大。注意到这些一次函数的斜率都大于零，这意味着如果分配完\(k\)后这些函数的取值不互相相等，那么可以把当前函数值最小的那个调大，当前函数值最大的那个调小，得到一个更优的答案。

因此我们要做的就是确定一条如下图所示的平行于\(x\)轴的直线，使得所有函数对应的\(x\)值之和为\(1\)。这样得到的解显然是合法的。

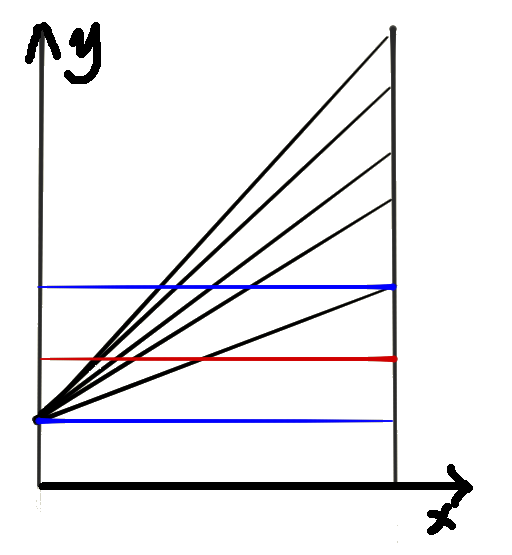
这当然可以二分。也能得到是根据以斜率的倒数为比例分配的。

这样就能\(O(n)\)解决本题了。

此外，这道题还有在笛卡尔树上dp的做法，与本做法没有太大区别。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> pii;
#define fir first
#define sec second
#define rep(i,a,b) for (int i = (a) ; i <= (b) ; ++ i)
#define rrp(i,a,b) for (int i = (a) ; i >= (b) ; -- i)
#define gc() getchar()
template <typename tp>
inline void read(tp& x) {
  x = 0; char tmp; bool key = 0;
  for (tmp = gc() ; !isdigit(tmp) ; tmp = gc())
    key = (tmp == '-');
  for ( ; isdigit(tmp) ; tmp = gc())
    x = (x << 3) + (x << 1) + (tmp ^ '0');
  if (key) x = -x;
}

const int N = 200010;
int ch[N << 1][26], fa[N << 1], len[N << 1], cnt = 1, las = 1;
bool tag[N << 1];
void append(char c) {
  int np = ++ cnt, p = las;
  tag[np] = 1;
  las = np;
  len[np] = len[p] + 1;
  fa[np] = 1;
  while (p && !ch[p][c - 'a'])
    ch[p][c - 'a'] = np, p = fa[p];
  if (!p) return;
  int q = ch[p][c - 'a'];
  if (len[q] == len[p] + 1)
    fa[np] = q;
  else {
    int nq = ++ cnt;
    len[nq] = len[p] + 1;
    tag[nq] = 0;
    fa[nq] = fa[q];
    rep (i, 0, 25) ch[nq][i] = ch[q][i];
    fa[q] = nq;
    fa[np] = nq;
    while (p && ch[p][c - 'a'] == q)
      ch[p][c - 'a'] = nq, p = fa[p];
  }
}
struct edge {
  int la,b;
} con[N << 1];
int tot,fir[N << 1];
void add(int from,int to) {
  con[++tot] = (edge) {fir[from], to};
  fir[from] = tot;
}
char str[N];
int n;
db dp[N << 1];
void dfs(int pos) {
  if (tag[pos]) {
    dp[pos] = len[pos];
    return;
  }
  db tmp = 0;
  for (int i = fir[pos] ; i ; i = con[i].la)
    dfs(con[i].b), tmp += 1.0 / (dp[con[i].b] - len[pos]);
  dp[pos] = 1.0 / tmp + len[pos];
}
void solve() {
  scanf("%s", str + 1);
  n = strlen(str + 1);
  tot = 0;
  las = cnt = 1;
  memset(fir,0,sizeof(int) * (2 * (n + 5)));
  memset(ch,0,sizeof(int) * (26 * 2 * (n + 5)));
  rrp (i, n, 1) append(str[i]);
  rep (i, 2, cnt) add(fa[i], i);
  dfs(1);
  printf("%.10lf\n", dp[1]);
}
int main() {
  int T;
  read(T);
  while (T --)
    solve();
  return 0;
}

小结：这种问题因为能把贡献规约到每个lca处，所以可以用树形dp解决。这和笛卡尔树的分治思路是同等的。