最短路径 SPFA P3371 【模板】单源最短路径（弱化版）

P3371 【模板】单源最短路径（弱化版）

SPFA算法：

SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同，为 O(VE)。

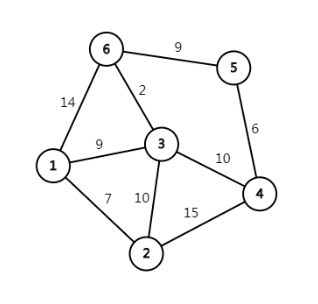
SPFA和Dijkstra不同的是：

Dijkstra  是从一个点的所有出边中找到一个最短出边，用它来继续更新下边的点

   SPFA     是用一个点的所有出边都更新它下面的点

更新之前把这个点存进队列

更新时把他拿出来，再把更新的出边终点（未入队的）入队

一直不断更新，直到队列为空

队列里存的是点

（下面有详细解释，在链式前向星以后）

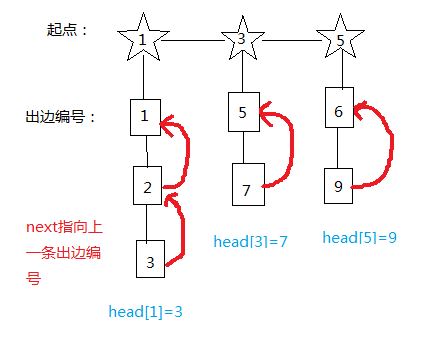
head[---]     这里大小根据点数决定
                    记录存边的历史，存的是i点的最后一条出边（它经历了不断更新）

vis[---]         判断是否已存入队列

 dis[---]         从起点开始到当前点的最短路径

num_edge  表示边的编号

这里要用链式前向星存图：

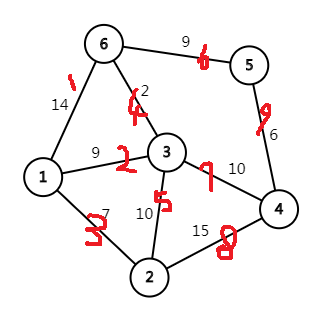
//以下为链式前向星存图
void addedge(int from,int to,int dis)   //存储每一条边 ：起点，终点，长度
{
    num_edge++;                         //新建一条边
    edge[num_edge].next=head[from];     //上一条出边
    edge[num_edge].to=to;
    edge[num_edge].dis=dis;
    head[from]=num_edge;                //记录最后一条出边
}

这里edge[1]=0，因为它是顶点1的第一条出边

edge[2]=1，edge[3]=2，

edge[5]=0，因为它是顶点5 的第一条出边

edge[7]=5

SPFA

默认起点是1

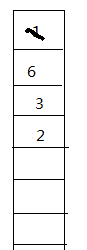用到1就把它弹出再用6更新5入队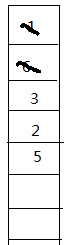再用3更新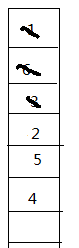

直到队列为空

【代码】：

#include<bits/stdc++.h>
#include<queue>
using namespace std;

const int inf=;

int n,m,s;
int dis[],vis[],head[],num_edge;

struct Edge
{
    int next,to,dis;
}edge[];  //大小由边数决定
// to   目标点
// dis  权值
// next 该点的上一条出边

queue<int>q;

//以下为链式前向星存图 
void addedge(int from,int to,int dis)   //存储每一条边 ： 起点，终点，长度
{
    num_edge++;                         //新建一条边
    edge[num_edge].next=head[from];     //上一条出边
    edge[num_edge].to=to;
    edge[num_edge].dis=dis;
    head[from]=num_edge;                //记录最后一条出边
}

void spfa()
{
    for(int i=;i<=n;i++)
    {
        dis[i]=inf;    //初始化最大值
        vis[i]=;      //都不入队
    }
    dis[s]=;
    vis[s]=;
    q.push(s);         //把起点S入队
    while(!q.empty())
    {
        int u=q.front();    //当前起点
        q.pop();            //用就弹出
        vis[u]=;           //弹出后记录为不在队列
        for(int i=head[u];i;i=edge[i].next)  //遍历起点的所有出边
        {
            int v=edge[i].to;   //当前终点
            if(dis[v]>dis[u]+edge[i].dis)  
            //如果【起点到当前终点的距离】>【起点到当前起点的距离＋当前距离与当前终点距离】
            //那就更新为更小距离
            {
                dis[v]=dis[u]+edge[i].dis;
                if(!vis[v])     //未入队的当前终点入队
                {
                    q.push(v);
                    vis[v]=;
                }
            }
        }
    }
}

int main()
{
    scanf("%d%d%d",&n,&m,&s);
    for(int i=;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        addedge(u,v,w);
    }
    spfa();
    for(int i=;i<=n;i++)
    {
        if(i==s)  printf("0 ");
        else printf("%d ",dis[i]);
     }
    return ;
}