2018牛客网暑假ACM多校训练赛（第二场）E tree 动态规划

原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round2-E.html

题目传送门 - 2018牛客多校赛第二场 E

题意

　　一棵 $n$ 个结点的树，每个点有一个点权，有 $m$ 次操作，每次操作有三种：

　　1.  修改一个点的点权

　　2.  修改一个点的父亲

　　3.  询问包含某个点的所有大小为 $c$ 的连通块的点权乘积之和。

　　$n,m\leq 100000,c\leq10 $

题解

　　　　

　　

　　
　　以上题解图片摘自 laofu 题解。

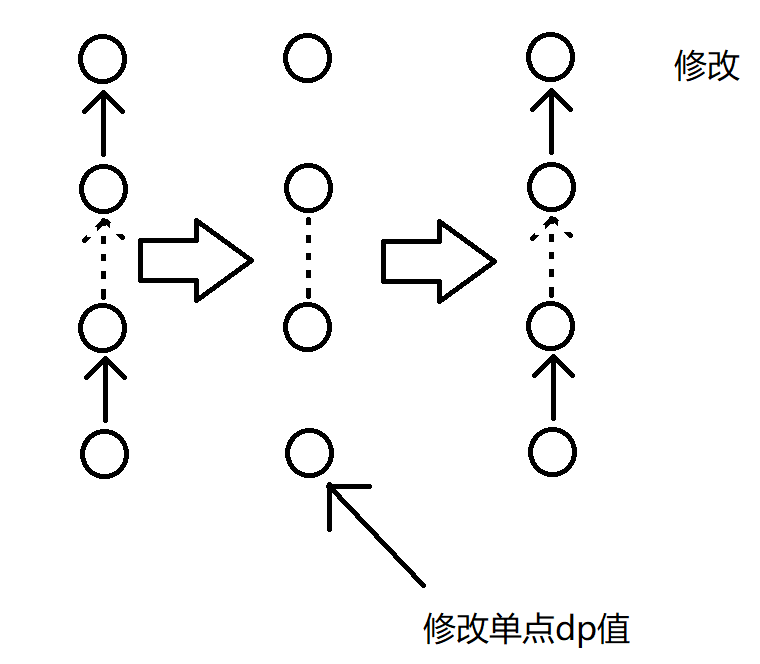
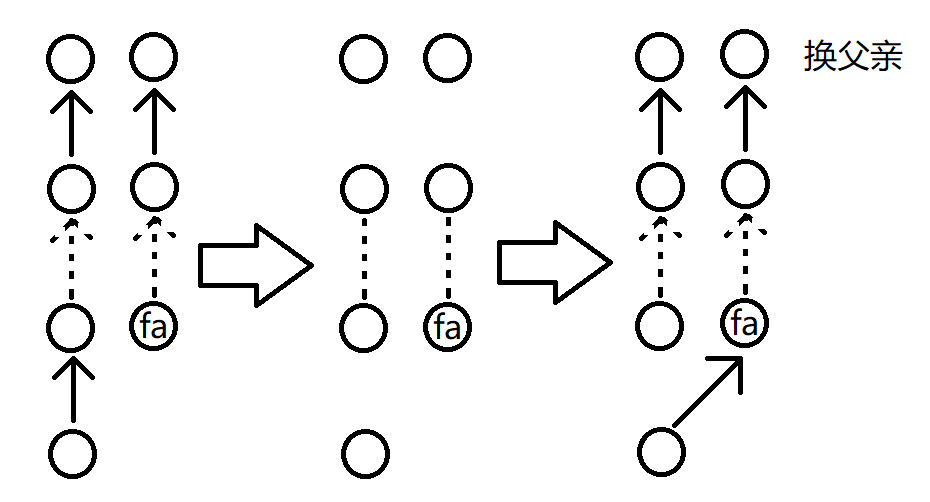
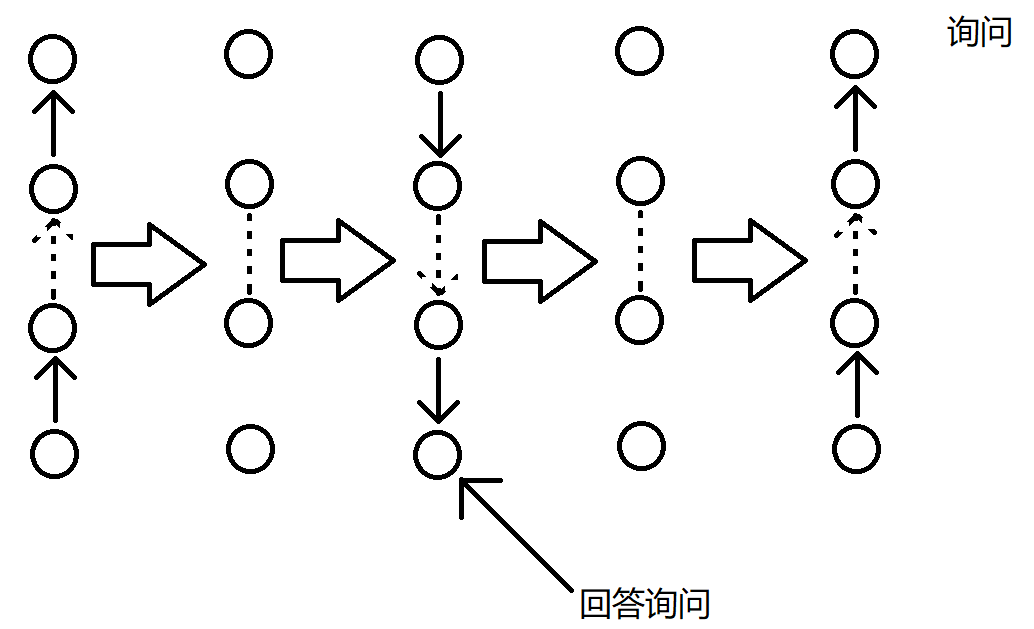
　　我再画几幅图介绍一下：

　　注：箭头表示箭头尾端节点的 dp 对箭头指向节点有 dp 贡献。

　　　　虚箭头表示中间省略一些有箭头连接的节点。

　　　　虚线表示中线省略一些节点，但是没有箭头连接。

　　　　每个图，最上面的节点表示往上走 $10$ 步到达的祖先。

　　　　最下面的节点表示操作中的 $x$ 节点。

　　　　注意一下修改和询问里面各有一个特殊箭头，意义自己理解。

　　

　　

代码

#include <bits/stdc++.h>
using namespace std;
int read(){
	char ch=getchar();
	int x=0;
	while (!isdigit(ch))
		ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+ch-48,ch=getchar();
	return x;
}
const int N=100005,mod=1e9+7;
int n,m,val[N],fa[N];
int dp[N][11];
int Pow(int x,int y){
	int ans=1;
	for (;y;y>>=1,x=1LL*x*x%mod)
		if (y&1)
			ans=1LL*ans*x%mod;
	return ans;
}
void DP(int a,int b){
	if (!a||!b)
		return;
	for (int i=10;i>=1;i--)
		for (int j=1;j<i;j++)
			dp[a][i]=(1LL*dp[a][i]+1LL*dp[a][j]*dp[b][i-j])%mod;
}
void IDP(int a,int b){
	if (!a||!b)
		return;
	for (int i=1;i<=10;i++)
		for (int j=1;j<i;j++)
			dp[a][i]=(1LL*dp[a][i]-1LL*dp[a][j]*dp[b][i-j])%mod;
}
int main(){
	n=read(),m=read();
	memset(dp,0,sizeof dp);
	for (int i=1;i<=n;i++)
		dp[i][1]=val[i]=read();
	for (int i=2;i<=n;i++)
		fa[i]=read();
	for (int i=n;i>1;i--)
		DP(fa[i],i);
	while (m--){
		int opt=read(),x=read(),y=read(),anc[15];
		if (opt==0){
			for (int i=1,j=x;i<=10;i++,j=fa[j])
				anc[i]=j;
			for (int i=10;i>1;i--)
				IDP(anc[i],anc[i-1]);
			int inv=Pow(val[x],mod-2);
			val[x]=y;
			for (int i=1;i<=10;i++)
				dp[x][i]=1LL*dp[x][i]*inv%mod*y%mod;
			for (int i=1;i<10;i++)
				DP(anc[i+1],anc[i]);
		}
		if (opt==1){
			for (int i=1,j=x;i<=10;i++,j=fa[j])
				anc[i]=j;
			for (int i=10;i>1;i--)
				IDP(anc[i],anc[i-1]);
			for (int i=2;i<10;i++)
				DP(anc[i+1],anc[i]);
			fa[x]=y;
			for (int i=1,j=x;i<=10;i++,j=fa[j])
				anc[i]=j;
			for (int i=10;i>2;i--)
				IDP(anc[i],anc[i-1]);
			for (int i=1;i<10;i++)
				DP(anc[i+1],anc[i]);
		}
		if (opt==2){
			for (int i=1,j=x;i<=10;i++,j=fa[j])
				anc[i]=j;
			for (int i=10;i>1;i--)
				IDP(anc[i],anc[i-1]);
			for (int i=10;i>1;i--)
				DP(anc[i-1],anc[i]);
			printf("%d\n",(dp[x][y]+mod)%mod);
			for (int i=1;i<10;i++)
				IDP(anc[i],anc[i+1]);
			for (int i=1;i<10;i++)
				DP(anc[i+1],anc[i]);
		}
	}
	return 0;
}