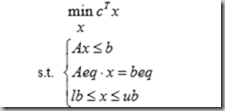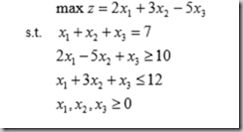【数学建模】day01-线性规划问题
线性规划问题是在一组线性约束条件下,求线性目标函数最大/最小值的问题。这些约束条件有不等式约束、等式约束以及边界约束,这和中学讲的线性规划无异。
此类问题的MATLAB标准形式为:
其中,max问题可以转换为min求解,三个约束条件分别为不等、等式、边界约束。
MATLAB求解函数:
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
param:
c是目标系数;
A、b对应不等条件;
Aeq、beq对用等式条件;
LB、UB为边界;
x0是求解的初始值;
OPTIONS是控制参数,一般不用。
return:
x向量是使得目标函数最小的x取值;
fval是相应的目标函数最优值,若是由max问题转化为min,还要取反。
例题以及matlab求解:
一、求解线性规划问题
求解的matlab程序如下:
f = [-2;-3;5];
A = [-2,5,-1;1,3,1];
b = [-10;12];
Aeq = [1,1,1];
beq = 7;
lb = [0;0;0];
ub = [inf;inf;inf];
[x,y]=linprog(f,A,b,Aeq,beq,zeros(3,1));
x
y = -y二、其他可以转换为线性规划问题,如目标为绝对值函数,指派问题(匈牙利算法),对偶理论与敏感度分析,在此略过,使用时查阅。
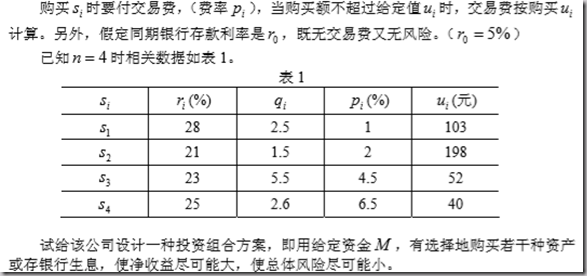
三、应用建模:投资的收益与风险
模型一的求解:
clc,clear
a = 0;
hold on
while a<0.05
c = [-0.05,-0.27,-0.19,-0.185,-0.185]
A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])];
b = a*ones(4,1);
Aeq = [1,1.01,1.02,1.045,1.065];
beq = 1;
LB = zeros(5,1);
[X,Q] = linprog(c,A,b,Aeq,beq,LB);
Q = -Q;
Q
plot(a,Q,'*k');
a = a + 0.001;
end
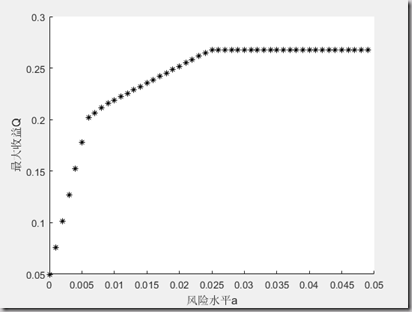
xlabel('风险水平a');
ylabel('最大收益Q');结果分析:
【数学建模】day01-线性规划问题的更多相关文章
- 【数学建模】线性规划各种问题的Python调包方法
关键词:Python.调包.线性规划.指派问题.运输问题.pulp.混合整数线性规划(MILP) 注:此文章是线性规划的调包实现,具体步骤原理请搜索具体解法. 本文章的各个问题可能会采用多种调用方 ...
- Python数学建模-02.数据导入
数据导入是所有数模编程的第一步,比你想象的更重要. 先要学会一种未必最佳,但是通用.安全.简单.好学的方法. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数据导入 ...
- Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
- BITED数学建模七日谈之二:怎样阅读数学模型教材
今天进入我们数学建模七日谈的第二天:怎样阅读数学建模教材? 大家再学习数学建模这门课程或准备比赛的时候,往往都是从教材开始的,教材的系统性让我们能够很快,很深入地了解前人在数学模型方面已有的研究成果, ...
- Python数学建模-01.新手必读
Python 完全可以满足数学建模的需要. Python 是数学建模的最佳选择之一,而且在其它工作中也无所不能. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数学 ...
- Python小白的数学建模课-A1.2021年数维杯C题(运动会优化比赛模式探索)探讨
Python小白的数学建模课 A1-2021年数维杯C题(运动会优化比赛模式探索)探讨. 运动会优化比赛模式问题,是公平分配问题 『Python小白的数学建模课 @ Youcans』带你从数模小白成为 ...
- Python小白的数学建模课-04.整数规划
整数规划与线性规划的差别只是变量的整数约束. 问题区别一点点,难度相差千万里. 选择简单通用的编程方案,让求解器去处理吧. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达 ...
- Python小白的数学建模课-A1.国赛赛题类型分析
分析赛题类型,才能有的放矢. 评论区留下邮箱地址,送你国奖论文分析 『Python小白的数学建模课 @ Youcans』 带你从数模小白成为国赛达人. 1. 数模竞赛国赛 A题类型分析 年份 题目 要 ...
- Python小白的数学建模课-05.0-1规划
0-1 规划不仅是数模竞赛中的常见题型,也具有重要的现实意义. 双十一促销中网购平台要求二选一,就是互斥的决策问题,可以用 0-1规划建模. 小白学习 0-1 规划,首先要学会识别 0-1规划,学习将 ...
- Python小白的数学建模课-A3.12 个新冠疫情数模竞赛赛题与点评
新冠疫情深刻和全面地影响着社会和生活,已经成为数学建模竞赛的背景帝. 本文收集了与新冠疫情相关的的数学建模竞赛赛题,供大家参考,欢迎收藏关注. 『Python小白的数学建模课 @ Youcans』带你 ...
随机推荐
- 【转】WPF PasswordBox不支持绑定解决方法
原文地址:https://www.cnblogs.com/wxjing67/p/3935717.html PasswordBox的Password属性因为安全原因不支持直接绑定,可以使用依赖属性实现. ...
- Microsoft.Extensions.DependencyInjection不同版本导致EF出现内存泄露。
我的代码里将IServiceProvider放入ServiceLocator中遇到的问题. 注:以下所有例子都是Console里的结论,AspNetCore里不管怎么玩都没有问题,有其他帖子测试出在A ...
- 微服务之:从零搭建ocelot网关和consul集群
介绍 微服务中有关键的几项技术,其中网关和服务服务发现,服务注册相辅相成. 首先解释几个本次教程中需要的术语 网关 Gateway(API GW / API 网关),顾名思义,是企业 IT 在系统边界 ...
- .NET Core 中正确使用 HttpClient 的姿势
为了更方便在服务端调用 HTTP 请求,微软在 .NET Framework 4.x 的时候引入了 HttpClient.但 HttpClient 有很多严重问题,一直饱受诟病,比如 InfoQ 的这 ...
- docker的4种网络模型
我们在使用docker run创建Docker容器时,可以用--net选项指定容器的网络模式,Docker有以下4种网络模式: · host模式,使用--net=host指定. · container ...
- SQL SERVER中的两种常见死锁及解决思路
在sql server中,死锁都与一种锁有关,那就是排它锁(x锁).由于在同一时间对同一个数据库资源只能有一个数据库进程可以拥有排它锁.因此,一旦多个进程都需要获取某个或者同一个数据库资源的排它访问权 ...
- Vue diff 算法
一.虚拟 DOM (virtual dom) diff 算法首先要明确一个概念就是 diff 的对象是虚拟DOM(virtual dom),更新真实 DOM 是 diff 算法的结果. 注:virtu ...
- Spring MVC普通类或工具类中调用service报空空指针的解决办法(调用service报java.lang.NullPointerException)
当我们在非Controller类中应用service的方法是会报空指针,如图: 这是因为Spring MVC普通类或工具类中调用service报空null的解决办法(调用service报java.la ...
- haoop笔记
: //:什么是hadoop? hadoop是解决大数据问题的一整套技术方案 :hadoop的组成? 核心框架 分布式文件系统 分布式计算框架 分布式资源分配框架 hadoop对象存储 机器计算 :h ...
- 搞站思路 <陆续完善中>
只提供思路经验分享.不提供日站方法....一般站点那里最容易出现问题 入手思路: 主站一般都很安全.一般从二级域名下手 多看看那些大站新出来的测试分站点 猜路径别忘了google 考虑看站点下的rob ...