吴恩达机器学习笔记 —— 7 Logistic回归
http://www.cnblogs.com/xing901022/p/9332529.html
本章主要讲解了逻辑回归相关的问题,比如什么是分类?逻辑回归如何定义损失函数?逻辑回归如何求最优解?如何理解决策边界?如何解决多分类的问题?
更多内容参考 机器学习&深度学习
有的时候我们遇到的问题并不是线性的问题,而是分类的问题。比如判断邮件是否是垃圾邮件,信用卡交易是否正常,肿瘤是良性还是恶性的。他们有一个共同点就是Y只有两个值{0,1},0代表正类,比如肿瘤是良性的;1代表负类,比如肿瘤是恶性的。当然你想用1代表良性也可以,而且输出的值不仅仅局限为0和1两类,有可能还有多类,比如手写体识别是从0到9。

如果使用线性的方法来判断分类问题,就会出现图上的问题。我们需要人工的判断中间的分界点,这个很不容易判断;如果在很远的地方有样本点,那么中心点就会发生漂移,影响准确性。

如果我们想要结果总是在0到1之间,那么就可以使用sigmoid函数,它能保证数据在0-1之间。并且越趋近于无穷大,数据越趋近于1。
回到我们假设的问题上来,如果肿瘤是依赖于大小来判断良性恶性,如果超过0.7*平均值,就判断是恶性的,那么平均来算30%的是恶性的,70%是良性的,他们相加总会是100%。再来看看上面的sigmoid的图像,每个点都表示它属于1的概率是x,属于0的概率是1-x。这样一个分类的问题,就变成了曲线值得问题了。
如果想让y=1,即g(z)的值要大于0.5,那么z的值就需要大于0;相反,y=0,就是z的值小于0。因此整个分类问题,就变成了寻找决策边界的问题了。
那么如何确定逻辑回归的损失函数呢?如果使用均方误差,由于最终的值都是0和1,就会产生震荡,此时是无法进行求导的。
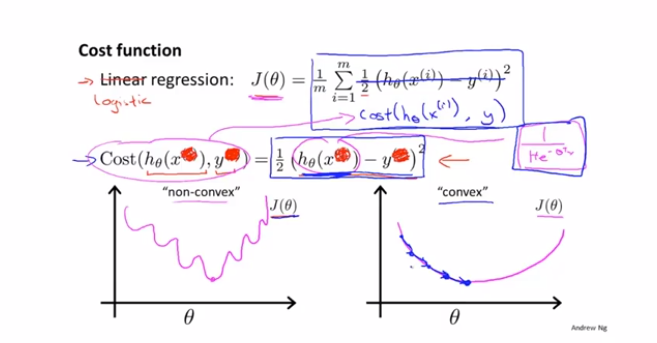
因此需要寻找一个方法,使得代价函数变成凸函数,从而易于求解。


如果把损失函数定义为上面的形式,当真实的值是1时,我们预测的值越靠近1,cost的值越小,误差越小。如果真实值是0,那么预测的值越靠近1,cost的值越大。完美的表达了损失的概念。而且,由于0和1的概念,可以把上面的公式合并成下面统一的写法。直接基于这个统一的写法,做梯度下降求解即可。

在求解最优化的问题时,不仅仅只有一种梯度下降Gradient descenet,还可以使用Conjugate gradient,BFGS,L-BFSGS。
多分类问题,可以理解为采用多个logistic分类器,进行分类。针对每个样本点进行一个预测,给出概率值,选择概率值最高的那个进行分类的标识。
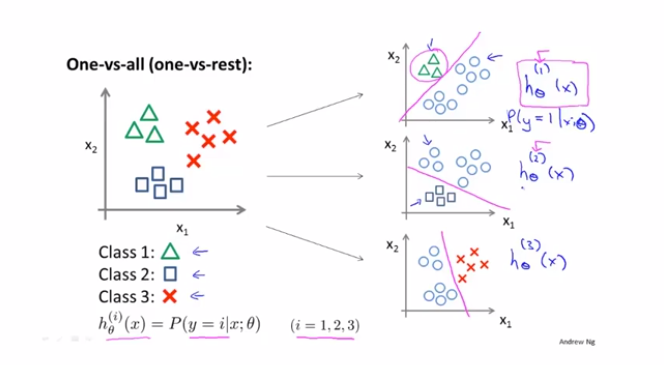
吴恩达机器学习笔记 —— 7 Logistic回归的更多相关文章
- 吴恩达机器学习笔记14-逻辑回归(Logistic Regression)
在分类问题中,你要预测的变量
- 吴恩达机器学习笔记(二) —— Logistic回归
主要内容: 一.回归与分类 二.Logistic模型即sigmoid function 三.decision boundary 决策边界 四.cost function 代价函数 五.梯度下降 六.自 ...
- 吴恩达机器学习笔记(三) —— Regularization正则化
主要内容: 一.欠拟合和过拟合(over-fitting) 二.解决过拟合的两种方法 三.正则化线性回归 四.正则化logistic回归 五.正则化的原理 一.欠拟合和过拟合(over-fitting ...
- 吴恩达机器学习笔记(四) —— BP神经网络
主要内容: 一.模型简介 二.一些变量所代表的含义 三.代价函数 四.Forward Propagation 五.Back Propagation 六.算法流程 待解决问题: 视频中通过指出:当特征变 ...
- 吴恩达机器学习笔记(九) —— 异常检测(Anomaly detection)
主要内容: 一.模型介绍 二.算法过程 三.算法性能评估及ε(threshold)的选择 四.Anomaly detection vs Supervised learning 五.Multivaria ...
- 吴恩达机器学习笔记(八) —— 降维与主成分分析法(PCA)
主要内容: 一.降维与PCA 二.PCA算法过程 三.PCA之恢复 四.如何选取维数K 五.PCA的作用与适用场合 一.降维与PCA 1.所谓降维,就是将数据由原来的n个特征(feature)缩减为k ...
- 吴恩达机器学习笔记(六) —— 支持向量机SVM
主要内容: 一.损失函数 二.决策边界 三.Kernel 四.使用SVM (有关SVM数学解释:机器学习笔记(八)震惊!支持向量机(SVM)居然是这种机) 一.损失函数 二.决策边界 对于: 当C非常 ...
- 吴恩达机器学习笔记22-正则化逻辑回归模型(Regularized Logistic Regression)
针对逻辑回归问题,我们在之前的课程已经学习过两种优化算法:我们首先学习了使用梯度下降法来优化代价函数
- [吴恩达机器学习笔记]12支持向量机1从逻辑回归到SVM/SVM的损失函数
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.1 SVM损失函数 从逻辑回归到支持向量机 为了描述 ...
随机推荐
- 从github上克隆hibernate项目
开发的项目用到了hibernate进行对象的持久化,最近项目上不忙,打算通过官方文档和源码来进行深度学习.第一步将hibernate部署到本地就折腾了好久,打算记录一下. 关于github的注册说一句 ...
- [部署]CentOS安装MariaDB
环境 虚拟机:VMWare10.0.1 build-1379776 操作系统:CentOS7 64位 步骤 1.添加MariaDB的yum仓库源,在/etc/yum.repos.d/ 下建立 Mari ...
- CSS3 Gradient 渐变还能这么玩
浏览器支持两种类型的渐变:线性渐变 (linear-gradient),径向渐变 (radial-gradient) 渐变在 CSS 中属于一种 Image 类型,可以结合 background-im ...
- SQLServer脚本编写
临时接到通知,需要临时编写一个SQL Server的脚本,供出差的同事使用一下. 我当时心想这个SQL Server脚本听都没听说过,但是组织说决定就是你了,那我就只能硬着头皮上了. 脚本实现的功能比 ...
- JS日期相减得到天数
废话不多说直奔主题,解决思路核心是时间戳相减 灵感来自于我经常用到一个工具方法:格式化时间,也是用时间戳 function GetNumberOfDays(date1,date2){//获得天数 / ...
- [java核心外篇]__Object类与对象类型的转型
前言 我们在之前的学习中提过很多次了,java是面向对象的,java的基础可以说是建立在类和对象上面的.然后我们又学到了类的继承,发现了在java类库中,类的继承是极为普遍的,一个类继承另一个类,就像 ...
- 用javascript写原生ajax(笔记)
AJAX 的全名叫做 Asynchronous JavaScript and XML(异步的 JavaScript 和 XML).它最大的优点是在不重新加载整个页面的情况下,可以与服务器交换数据并 ...
- Java网络编程的基本网络概念
前言 自己网络这方面的知识很是薄弱,每次面试被问到这部分都会卡壳,所以很尴尬,然后最近也是有些时间了,就赶紧把自己的不足补充一下.虽然最近也在看设计模式,但是总看设计模式也容易烦,所以就并行学习,看看 ...
- JavaScript基础知识梳理,你能回答几道题?
在学习JavaScript的时候,总是这里学一点,那里学一点,很的很零星,很杂,没有很系统的去学习,感觉好像JavaScript的知识点都了解了,但是真正要说起来,又不知道从何说起! 最深刻的体会就是 ...
- [转]How To Send Transactional Email In A NodeJS App Using The Mailgun API
https://www.npmjs.com/package/mailgun-js 本文转自:https://www.mailgun.com/blog/how-to-send-transactional ...
