bzoj2194 快速傅里叶之二

题意：对于k = 0 ... n求

解：

首先把i变成从0开始

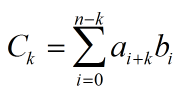
我们发现a和b的次数(下标)是成正比例的，这不可，于是反转就行了。

反转b的话，会发现次数和是n + k，这不可。

反转a就很吼了。

这个东西恰好是卷积出来的第n - k项的系数。

所以我们把a串反转，然后用a与b卷积，最后再反转输出即可。

 /**************************************************************
     Problem: 2194
     Language: C++
     Result: Accepted
     Time:133643896 ms
     Memory:14342474884 kb
 ****************************************************************/

 #include <cstdio>
 #include <algorithm>
 #include <cmath>
 #include <cstring>

 const int N = ;
 const double pi = 3.1415926535897932384626;

 struct cp {
     double x, y;
     cp(double X = , double Y = ) {
         x = X;
         y = Y;
     }
     inline cp operator +(const cp &w) const {
         return cp(x + w.x, y + w.y);
     }
     inline cp operator -(const cp &w) const {
         return cp(x - w.x, y - w.y);
     }
     inline cp operator *(const cp &w) const {
         return cp(x * w.x - y * w.y, x * w.y + y * w.x);
     }
 }a[N << ], b[N << ];

 int r[N << ];

 inline void FFT(int n, cp *a, int f) {
     for(int i = ; i < n; i++) {
         if(i < r[i]) {
             std::swap(a[i], a[r[i]]);
         }
     }

     for(int len = ; len < n; len <<= ) {
         cp Wn(cos(pi / len), f * sin(pi / len));
         for(int i = ; i < n; i += (len << )) {
             cp w(, );
             for(int j = ; j < len; j++) {
                 cp t = a[i + len + j] * w;
                 a[i + len + j] = a[i + j] - t;
                 a[i + j] = a[i + j] + t;
                 w = w * Wn;
             }
         }
     }

     if(f == -) {
         for(int i = ; i <= n; i++) {
             a[i].x /= n;
         }
     }
     return;
 }

 int main() {
     int n;
     scanf("%d", &n);
     n--;
     for(int i = ; i <= n; i++) {
         scanf("%lf%lf", &a[n - i].x, &b[i].x);
     }

     int len = , lm = ;
     while(len <= (n << )) {
         len <<= ;
         lm++;
     }
     for(int i = ; i <= len; i++) {
         r[i] = (r[i >> ] >> ) | ((i & ) << (lm - ));
     }

     FFT(len, a, );
     FFT(len, b, );
     for(int i = ; i <= len; i++) {
         a[i] = a[i] * b[i];
     }
     FFT(len, a, -);

     for(int i = ; i <= n; i++) {
         printf("%d\n", (int)(a[n - i].x + 0.5));
     }

     return ;
 }

AC代码