【bzoj1069】最大土地面积

Description

　　在某块平面土地上有N个点，你可以选择其中的任意四个点，将这片土地围起来，当然，你希望这四个点围成
的多边形面积最大。

Input

　　第1行一个正整数N，接下来N行，每行2个数x,y，表示该点的横坐标和纵坐标。

Output

　　最大的多边形面积，答案精确到小数点后3位。

Sample Input

5
0 0
1 0
1 1
0 1
0.5 0.5

Sample Output

1.000

HINT

数据范围 n<=2000, |x|,|y|<=100000

Solution

显然四个点都在凸包上啊！

显然的，我们枚举对角线，我们现在的问题是找离对角线最远的点是哪两个点

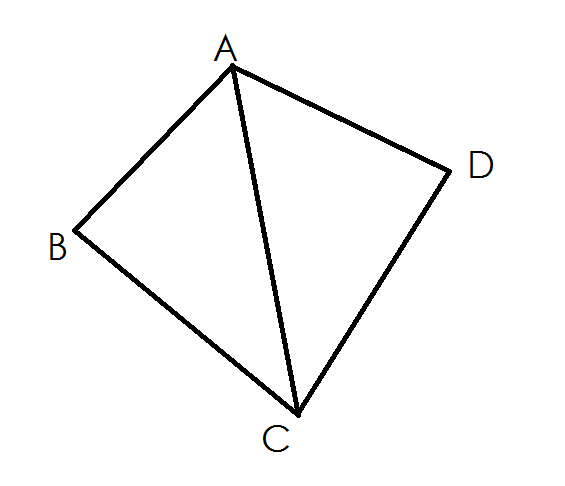
于是我们发现，当A固定，C变为逆时针的下一个点的时候，

B,D也一定是单调逆时针变动的

这里运用旋转卡壳的思想

所以这题本质是旋转卡壳，只是更加简单了

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define il inline
#define re register
using namespace std;
typedef double db;
const int N=;
const db eps=1e-;
struct P{db x,y;} a[N],s[N];
int n,top;db ans=;
il P operator-(P a,P b){
    return (P){a.x-b.x,a.y-b.y};
}
il db operator*(P a,P b){
    return a.x*b.y-a.y*b.x;
}
il db S(P a,P b,P c){
    return fabs((a-b)*(a-c))/;
}
il db dis(P a){
    return a.x*a.x+a.y*a.y;
}
il db cmp(P x,P y){
    return (x-a[])*(y-a[])>;
}
il void print(P a){
    printf("(%lf,%lf)\n",a.x,a.y);
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%lf%lf",&a[i].x,&a[i].y);
    }
    for(int i=;i<=n;i++)
        if(a[i].y<a[].y||(a[i].y==a[].y&&a[i].x<a[].x)) swap(a[],a[i]);
    sort(a+,a+n+,cmp);
    s[]=a[];s[]=a[];top=;
    for(int i=;i<=n;i++){
        while(top>&&(a[i]-s[top-])*(s[top]-s[top-])>=) top--;
        s[++top]=a[i];
    }
    if(top==){
        ans=S(s[],s[],s[])+S(s[],s[],s[]);
        printf("%.3lf",ans);
        return ;
    }
//    for(int i=1;i<=top;i++) print(s[i]);
    for(int i=;i<top;i++) s[i]=s[i+];
    n=top;
    for(int i=;i<n;i++){
        for(int j=(i+)%n,k=(i+)%n,l=(i+)%n;k!=(i-+n)%n;k=(k+)%n){
            while(S(s[i],s[j],s[k])<S(s[i],s[(j+)%n],s[k])) j=(j+)%n;
            while(S(s[i],s[l],s[k])<S(s[i],s[(l+)%n],s[k])) l=(l+)%n;
        //    cout<<i<<" "<<j<<" "<<k<<" "<<l<<endl;
            ans=max(S(s[i],s[j],s[k])+S(s[i],s[k],s[l]),ans);
        }
    }
    printf("%.3lf",ans);
    return ;
}