齐夫定律， Zipf's law，Zipfian distribution

齐夫定律（英语：Zipf's law，IPA英语发音：/ˈzɪf/）是由哈佛大学的语言学家乔治·金斯利·齐夫（George Kingsley Zipf）于1949年发表的实验定律。

它可以表述为：

在自然语言的语料库里，一个单词出现的频率与它在频率表里的排名成反比。

所以，频率最高的单词出现的频率大约是出现频率第二位的单词的2倍，

而出现频率第二位的单词则是出现频率第四位的单词的2倍。

这个定律被作为任何与幂定律概率分布有关的事物的参考。

目录

• 1 例子
• 2 遵循该定律的现象
• 3 参见
• 4 延伸阅读
• 5 外部链接

例子

最简单的齐夫定律的例子是“1/f function”。给出一组齐夫分布的频率，按照从最常见到非常见排列，第二常见的频率是最常见频率的出现次数的½，第三常见的频率是最常见的频率的1/3，第n常见的频率是最常见频率出现次数的1/n。然而，这并不精确，因为所有的项必须出现一个整数次数，一个单词不可能出现2.5次。

在Brown语料库中，“the”、“of”、“and”是出现频率最前的三个单词，其出现的频数分别为69971次、36411次、28852次，大约占整个语料库100万个单词中的7%、3.6%、2.9%，其比例约为6：3：2。大约占整个语料库的7%（100万单词中出现69971次）。满足齐夫定律中的描述。仅仅前135个字汇就占了Brown语料库的一半。

齐夫定律是一个实验定律，而非理论定律，可以在很多非语言学排名中被观察到，例如不同国家中城市的数量、公司的规模、收入排名等。但它的起因是一个争论的焦点。齐夫定律很容易用点阵图观察，坐标分别为排名和频率的自然对数（log）。比如，“the”用上述表述可以描述为x = log(1), y = log（69971）的点。如果所有的点接近一条直线，那么它就遵循齐夫定律。

遵循该定律的现象

• 单词的出现频率:不仅适用于语料全体,也适用于单独的一篇文章
• 网页访问频率
• 城市人口
• 收入前3%的人的收入
• 地震震级
• 固体破碎时的碎片大小

参见

• 经验公式

====================================

Zipf Distribution

The Zipf distribution, sometimes referred to as the zeta distribution, is a discrete distribution commonly used in linguistics, insurance, and the modelling of rare events. It has probability density function

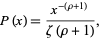where 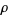is a positive parameter and 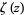is the Riemann zeta function, and distribution function

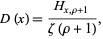where 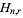is a generalized harmonic number.

The Zipf distribution is implemented in the Wolfram Language as ZipfDistribution[rho].

The 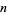th raw moment is

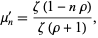giving the mean and variance as

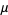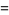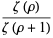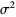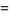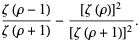The distribution has mean deviation

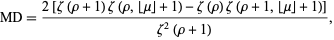where 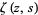is a Hurwitz zeta function and 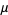is the mean as given above in equation (4).

SEE ALSO: Zipf's Law

 

CITE THIS AS: Weisstein, Eric W. "Zipf Distribution." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ZipfDistribution.html

Zipf's Law

In the English language, the probability of encountering the 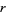th most common word is given roughly by 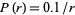for 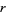up to 1000 or so. The law breaks down for less frequent words, since the harmonic series diverges. Pierce's (1980, p. 87) statement that 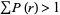for 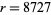is incorrect. Goetz states the law as follows: The frequency of a word is inversely proportional to its statistical rank 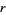such that

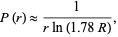where 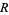is the number of different words.

Theoretical review

Zipf's law is most easily observed by plotting the data on a log-log graph, with the axes being log (rank order) and log (frequency). For example, the word "the" (as described above) would appear at x = log(1), y = log(69971). It is also possible to plot reciprocal rank against frequency or reciprocal frequency or interword interval against rank.^[1] The data conform to Zipf's law to the extent that the plot is linear.

Formally, let:

• N be the number of elements;
• k be their rank;
• s be the value of the exponent characterizing the distribution.

Zipf's law then predicts that out of a population of N elements, the frequency of elements of rank k, f(k;s,N), is:

f ( k ; s , N ) = 1 / k s ∑ n = 1 N ( 1 / n s ) {\displaystyle f(k;s,N)={\frac {1/k^{s}}{\sum _{n=1}^{N}(1/n^{s})}}}

•