【洛谷 5002】专心OI - 找祖先 （树上计数）

专心OI - 找祖先

题目背景

\(Imakf\)是一个小蒟蒻，他最近刚学了\(LCA\)，他在手机\(APP\)里看到一个游戏也叫做\(LCA\)就下载了下来。

题目描述

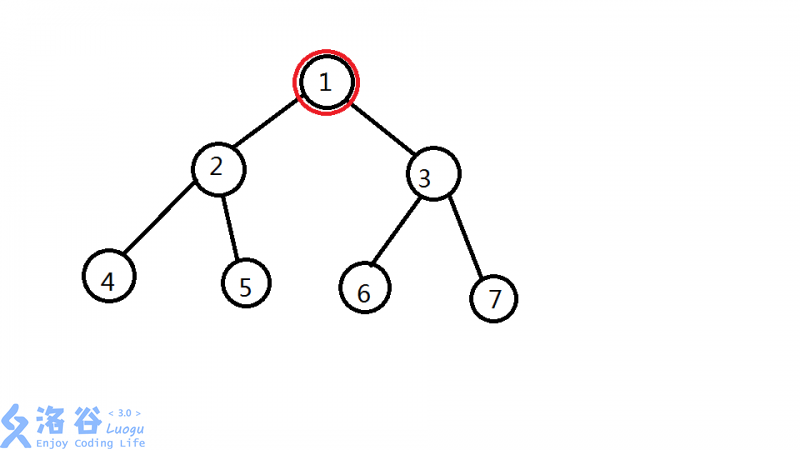
这个游戏会给出你一棵树，这棵树有\(N\)个节点，根结点是\(R\)，系统会选中\(M\)个点\(P_1,P_2...P_M\)，要\(Imakf\)回答有多少组点对\((u_i,v_i)\)的最近公共祖先是\(P_i\)。\(Imakf\)是个小蒟蒻，他就算学了\(LCA\)也做不出，于是只好求助您了。

\(Imakf\)毕竟学过一点\(OI\),所以他允许您把答案模 \((10^9+7)\)

输入输出格式

输入格式：

第一行 \(N , R , M\).

此后\(N-1\)行 每行两个数\(a,b\) 表示\(a,b\)之间有一条边

此后\(1\)行 \(M\)个数 表示\(P_i\)

输出格式：

\(M\)行，每行一个数，第ii行的数表示有多少组点对\((u_i,v_i)\)的最近公共祖先是\(P_i\)

输入输出样例

输入样例#1：

7 1 3
1 2
1 3
2 4
2 5
3 6
3 7
1 2 4

输出样例#1：

31
7
1

说明

对于询问1：

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (1,7) (2,1) (2,3) (2,6) (2,7) (3,1) (3,2) (3,4) (3,5) (4,1) (4,3) (4,6) (4,7) (5,1) (5,3) (5,6) (5,7) (6,1) (6,2) (6,4) (6,5) (7,1) (7,2) (7,4) (7,5)共31组

对于询问2：

(2,2) (2,4) (2,5) (4,2) (4,5) (5,2) (5,4)共7组

对于询问3:

(4,4)共1组

数据范围

\(N\leq10000,M\leq50000\)

题解

看到这是洛谷新出的题，看着有点思路就做了。

我在\(dfs\)时就预处理出了\(ans\)数组，即为每个点的答案，所以时间复杂度是\(O(max(n,m))\)

对于每个点\(x\)，我们可以把答案分成跨过\(x\)的和没有跨过\(x\)的方案两部分。

没有跨过x的部分：

很显然，其中一个点一定是\(x\)，所以这部分的答案为\(x\)的\(siz\)大小的\(2\)倍\(-1\)（因为是点对并且(1,1)算一种）。

即\(ans1=2*siz[x]-1\).

跨过\(x\)的部分:

根据乘法原理，所有\(x\)的儿子\(son_i\)的\(siz\)大小相乘即为这部分的答案。

设\(x\)一共有\(k\)棵子树即

\[ans2=\sum_{i=1}^{k}\sum_{j=1}^{k}siz[son[i]]*siz[son[j]] \\=\sum_{i=1}^{k}siz[son[i]]*(siz[x]-1)\\=(siz[x]-1)*(siz[x]-1)
\]

但是我们会发现不对，因为我们算重了一部分，就是\((i==j)\)的部分。

所以我们还要减去\(\sum_{i=1}^{k}siz[son[i]]^2\).

所以\(ans2=(siz[x]-1)^2-\sum_{i=1}^{k}siz[son[i]]^2\)

综上：

\[Ans=ans1+ans2\\=2*siz[x]-1+(siz[x]-1)^2-\sum_{i=1}^{k}siz[son[i]]^2\\=siz[x]^2-\sum_{i=1}^{k}siz[son[i]]^2
\]

我们只需要维护一下每个点子树的\(siz[son[i]]^2\)的和即可获得答案。

吐槽一句：这题Ans最大是\(N^2\)，居然要去取模。。。。

code：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cctype>
#include<cstring>
#define N 10005
#define R register
using namespace std;
template<typename T>inline void read(T &a){
    char c=getchar();T x=0,f=1;
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    a=f*x;
}
int n,rt,m,tot,p;
int siz[N],ans[N],h[N],sum[N];
struct node{
    int nex,to;
}edge[N<<1];
inline void add(R int u,R int v){
    edge[++tot].nex=h[u];
    edge[tot].to=v;
    h[u]=tot;
}
inline void dfs(R int x,R int f){
    siz[x]=1;
    for(R int i=h[x];i;i=edge[i].nex){
        R int xx=edge[i].to;
        if(xx==f)continue;
        dfs(xx,x);
        siz[x]+=siz[xx];
        sum[x]+=siz[xx]*siz[xx];
    }
    ans[x]=siz[x]*siz[x]-sum[x];
}
int main(){
    read(n);read(rt);read(m);
    for(R int i=1,u,v;i<=n-1;i++)
        read(u),read(v),add(u,v),add(v,u);
    dfs(rt,0);
    while(m--){
    	read(p);
    	printf("%d\n",ans[p]);
    }
    return 0;
}