【十大经典数据挖掘算法】SVM

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

SVM（Support Vector Machines）是分类算法中应用广泛、效果不错的一类。《统计学习方法》对SVM的数学原理做了详细推导与论述，本文仅做整理。由简至繁SVM可分类为三类：线性可分（linear SVM in linearly separable case）的线性SVM、线性不可分的线性SVM、非线性（nonlinear）SVM。

1. 线性可分

对于二类分类问题，训练集\(T = \lbrace (x_1,y_1),(x_2,y_2), \cdots ,(x_N,y_N) \rbrace\)，其类别\(y_i \in \lbrace 0,1 \rbrace\)，线性SVM通过学习得到分离超平面（hyperplane）:

\[
w \cdot x + b =0
\]

以及相应的分类决策函数：

\[
f(x)=sign(w \cdot x + b)
\]

有如下图所示的分离超平面，哪一个超平面的分类效果更好呢？

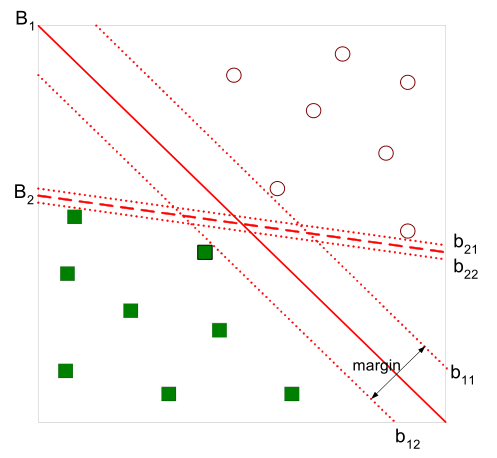
直观上，超平面\(B_1\)的分类效果更好一些。将距离分离超平面最近的两个不同类别的样本点称为支持向量（support vector）的，构成了两条平行于分离超平面的长带，二者之间的距离称之为margin。显然，margin更大，则分类正确的确信度更高（与超平面的距离表示分类的确信度，距离越远则分类正确的确信度越高）。通过计算容易得到：

\[
margin = \frac{2}{\|w\|}
\]

从上图中可观察到：margin以外的样本点对于确定分离超平面没有贡献，换句话说，SVM是有很重要的训练样本（支持向量）所确定的。至此，SVM分类问题可描述为在全部分类正确的情况下，最大化\(\frac{2}{\|w\|}\)（等价于最小化\(\frac{1}{2}\|w\|^2\)）；线性分类的约束最优化问题：

\begin{align}
& \min_{w,b} \quad \frac{1}{2}\|w\|^2 \cr
& s.t. \quad y_i(w \cdot x_i + b)-1 \ge 0 \label{eq:linear-st}
\end{align}

对每一个不等式约束引进拉格朗日乘子（Lagrange multiplier）\(\alpha_i \ge 0, i=1,2,\cdots,N\)；构造拉格朗日函数（Lagrange function）：

\begin{equation}
L(w,b,\alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^{N}\alpha_i [y_i(w \cdot x_i + b)-1] \label{eq:lagrange}
\end{equation}

根据拉格朗日对偶性，原始的约束最优化问题可等价于极大极小的对偶问题：

\[
\max_{\alpha} \min_{w,b} \quad L(w,b,\alpha)
\]

将\(L(w,b,\alpha)\)对\(w,b\)求偏导并令其等于0，则

\[
\begin{aligned}
& \frac{\partial L}{\partial w} = w-\sum_{i=1}^{N}\alpha_i y_i x_i =0 \quad \Rightarrow \quad w = \sum_{i=1}^{N}\alpha_i y_i x_i \cr
& \frac{\partial L}{\partial b} = \sum_{i=1}^{N}\alpha_i y_i = 0
\quad \Rightarrow \quad \sum_{i=1}^{N}\alpha_i y_i = 0
\end{aligned}
\]

将上述式子代入拉格朗日函数\eqref{eq:lagrange}中，对偶问题转为

\[
\max_{\alpha} \quad -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^{N}\alpha_i
\]

等价于最优化问题：

\begin{align}
\min_{\alpha} \quad & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_i \cr
s.t. \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \cr
& \alpha_i \ge 0, \quad i=1,2,\cdots,N
\end{align}

线性可分是理想情形，大多数情况下，由于噪声或特异点等各种原因，训练样本是线性不可分的。因此，需要更一般化的学习算法。

2. 线性不可分

线性不可分意味着有样本点不满足约束条件\eqref{eq:linear-st}，为了解决这个问题，对每个样本引入一个松弛变量\(\xi_i \ge 0\)，这样约束条件变为：

\[
y_i(w \cdot x_i + b) \ge 1- \xi_i
\]

目标函数则变为

\[
\min_{w,b,\xi} \quad \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{N} \xi_i
\]

其中，\(C\)为惩罚函数，目标函数有两层含义：

• margin尽量大，
• 误分类的样本点计量少

\(C\)为调节二者的参数。通过构造拉格朗日函数并求解偏导（具体推导略去），可得到等价的对偶问题：

\begin{equation}
\min_{\alpha} \quad \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum_{i=1}^{N} {\alpha_i} \label{eq:svmobj}
\end{equation}

\begin{align}
s.t. \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \cr
& 0 \le \alpha_i \le C, \quad i=1,2,\cdots,N
\end{align}

与上一节中线性可分的对偶问题相比，只是约束条件\(\alpha_i\)发生变化，问题求解思路与之类似。

3. 非线性

对于非线性问题，线性SVM不再适用了，需要非线性SVM来解决了。解决非线性分类问题的思路，通过空间变换\(\phi\)（一般是低维空间映射到高维空间\(x \rightarrow \phi(x)\)）后实现线性可分，在下图所示的例子中，通过空间变换，将左图中的椭圆分离面变换成了右图中直线。

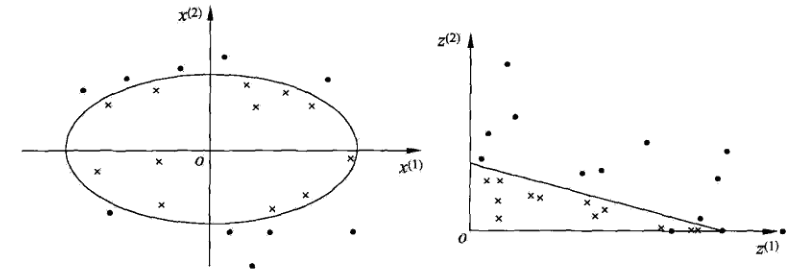
在SVM的等价对偶问题中的目标函数中有样本点的内积\(x_i \cdot x_j\)，在空间变换后则是\(\phi(x_i) \cdot \phi(x_j)\)，由于维数增加导致内积计算成本增加，这时核函数（kernel function）便派上用场了，将映射后的高维空间内积转换成低维空间的函数：

\[
K(x,z)=\phi(x) \cdot \phi(z)
\]

将其代入一般化的SVM学习算法的目标函数\eqref{eq:svmobj}中，可得非线性SVM的最优化问题：

\begin{align}
\min_{\alpha} \quad & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(x_i,x_j) - \sum_{i=1}^{N}\alpha_i \cr
s.t. \quad & \sum_{i=1}^{N}\alpha_i y_i = 0 \cr
& 0 \le \alpha_i \le C, \quad i=1,2,\cdots,N
\end{align}

4. 参考资料

[1] 李航，《统计学习方法》.
[2] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.