【现代程序设计】【homework-03】【11061027】
Q:你现在使用的代码规范是什么, 和上课前有什么改进?
A: 代码规范........自定义的代码规范算 代码规范吗。。。。。
Q:你的同伴有哪些优点 (列出至少三点), 和那些需要改进的地方 (列出至少三点)
A:
Q:你的代码从 作业2 到 作业3 经历了哪些变化? 哪些代码需要重构 (看关于代码重构的资料), 哪些需要重写, 为什么?
A:因为作业2是用c写的,作业3用c#(wpf)写的,我打算做一个界面交互,而非命令行的maxsum,所以作业3的代码是基本上都是重写的
Q:你的设计是如何保证 不同的 maxsum.exe 命令行最后在一个GUI 的界面显示的?
A:由于做的是界面操作的应用,命令行显的不实用和麻烦,所以我没加入命令行这个功能,也就不存在【不同的 maxsum.exe 命令行最后在一个GUI 的界面显示的】的问题
|
Personal Software Process Stages |
时间百分比(%) |
实际花费的时间 (分钟) |
原来估计的时间 (分钟) |
|
|
计划 |
||||
|
· 估计这个任务需要多少时间,把工作细化并大致排序 |
0 | 0 | 0 | |
|
开发 |
||||
|
· 需求分析 (包括学习新技术) |
20 | 3h | 1h | |
|
· 生成设计文档 |
0 | 0 | 0 | |
|
· 设计复审 (和同事审核设计文档) |
0 | 0 | 0 | |
|
· 代码规范 (制定合适的规范) |
0 | 0 | 0 | |
|
· 具体设计 |
15 | 3h | 2h | |
|
· 具体编码 |
20 | 3h | 6h | |
|
· 代码复审 |
10 | 2h | 2h | |
|
· 测试(自我测试,修改代码,提交修改) |
35 | 7h | 4h | |
|
总结报告 |
||||
| Total | 总计 | 100% | 总用时 18h | 总估计的用 15h |
总结:
因为对WPF不太熟悉,所以这次作业很多的时间花在了学习wpf上
一开始挑选显示二维数组的Xaml控件,google了半天,感觉好像是 DataGrid更方便一点。
然后就用datagrid显示二维数组
单独改变DataGrid的某个cell的背景色不会,Google了好一会
然后因为这个DataDrid的行列都是动态确定的,数据绑定又Google了好一会.....
在花了不少的时间搞定UI这一块之后 ,很快搞定了【子矩阵的问题】和【连通子图】
运行的时候发现,由于上次作业【连通子图】写的太懒,就一个递归,什么剪枝都没有 ,于是代码的时间效率实在是 渣
又重新写了一个【连通子图】的类,并重做了优化,这点又花了很长时间
虽然时间效率还是很渣,但是勉强还是解出来
最后就是烦人的测试,Debug...文件输入的Debug,AnyMaxsum的Debug,Maxsum的Debug,UI显示的Debug。。。
然后现在总算是完成了
下面是anymaxsum的c#代码
通过 GetResultData()获取 数据
namespace maxsum
{
class AnyMaxsum
{
bool[,] gTemp,gResult;
bool isvselect=false, ishselect=false;
int sumall=,n,m,cpuload,amax;
public int sum=-, nsum = ; int[,] a, asum, gmain;
int[] dx={-,,,},dy={,-,,}; void init()
{
for (int i = ; i < m; i++)
for (int j = ; j < n; j++)
{
gTemp[i, j] = gResult[i, j] = false;
gmain[i, j] = ;
} } public AnyMaxsum(int Arrm,int Arrn,int[,] ArrSource)
{
n = Arrn;
m = Arrm;
a = new int[m, n];
asum = new int[m, n]; gTemp = new bool[m, n];
gmain = new int[m, n];
gResult = new bool[m, n]; a = ArrSource;
for (int i = ; i < m; i++)
for (int j = ; j < m; j++)
{
if (a[i, j] > ) sumall += a[i, j];
asum[i, j] = sumall;
if (amax < a[i, j]) amax = a[i, j];
} } public void setvh(bool v,bool h)
{
isvselect = v;
ishselect = h;
} public void GetResultData(ref int s,ref bool[,] aresult)
{
init();
if (sumall <= )
{
int x = , y = , z = -;
for (int i = ; i < m; i++)
for (int j = ; j < n; j++) if (z < a[i, j])
{
z = a[i, j];
x = i;
y = j;
}
s = z;
for (int i = ; i < m; i++)
for (int j = ; j < n; j++) aresult[i, j] = false;
aresult[x, y] = true;
return;
} fany(, -, );
for (int i = ; i < m; i++)
for (int j = ; j < n; j++) aresult[i, j] = gResult[i, j];
s = sum;
}
public int GetCpuLoad()
{
return cpuload;
} bool isinvh(int x,int y)
{
if (x >= && x < m && y >= && y < n)
return true;
return false;
} void ff(int x, int y)
{
int tx, ty, i; gTemp[x, y] = true; for (i = ; i < ; i++)
{
tx = x + dx[i];
ty = y + dy[i]; if (isvselect)
{
if (tx == m) tx = ;
if (tx == -) tx = m - ;
} if (ishselect)
{
if (ty == n) ty = ;
if (ty == -) ty = n - ;
} if (isinvh(tx, ty) && !gTemp[tx,ty] && gmain[tx,ty]<)
ff(tx, ty);
}
} void fany(int x, int y, int z)
{
int tx, ty, tt, i, j; cpuload++; for (i = ; i <= x; i++)
for (j = ; j < n; j++)
if (gmain[i, j] == )
{
tx = i; ty = j;
for (i = ; i < m; i++)
for (j = ; j < n; j++) gTemp[i, j] = false;
ff(tx, ty);
for (i = ; i <= x; i++)
for (j = ; j < n; j++) if (!gTemp[i, j] && gmain[i, j] == ) return;
i = x + ;
break;
} if (x == m - && y == n - )
{ if (sum > z) return; tt = ;
for (i = ; i < m; i++)
for (j = ; j < n; j++) if (gmain[i, j] == )
tt++; if (sum == z && tt > nsum) return; for (i = ; i < m; i++)
for (j = ; j < n; j++) if (gmain[i, j] == )
gResult[i, j] = true;
else gResult[i, j] = false; sum = z;
nsum = tt;
return;
} ty = (y + ) % n;
tx = x + (y + ) / n; tt = sumall - asum[tx, ty] + z; if (tt + a[tx, ty] >= sum)
{
gmain[tx, ty] = ;
fany(tx, ty, z + a[tx, ty]);
gmain[tx, ty] = ;
}
if (tt >= sum)
{
gmain[tx, ty] = ;
fany(tx, ty, z);
gmain[tx, ty] = ;
}
} }
}
下面是工程文件和截图和测试数据:
测试数据:我一共写了14组测试数据,加上xinz老师的4组,18组测试数据
http://files.cnblogs.com/lightz/MaxsumTestData.zip
VS2012_工程文件:maxsum软件 包含在文件的bin\Release 目录下
http://files.cnblogs.com/lightz/Maxsum_VS2012.zip
截图:
http://files.cnblogs.com/lightz/Maxsum%E6%88%AA%E5%9B%BE.zip
这里随便贴了几张,如下:

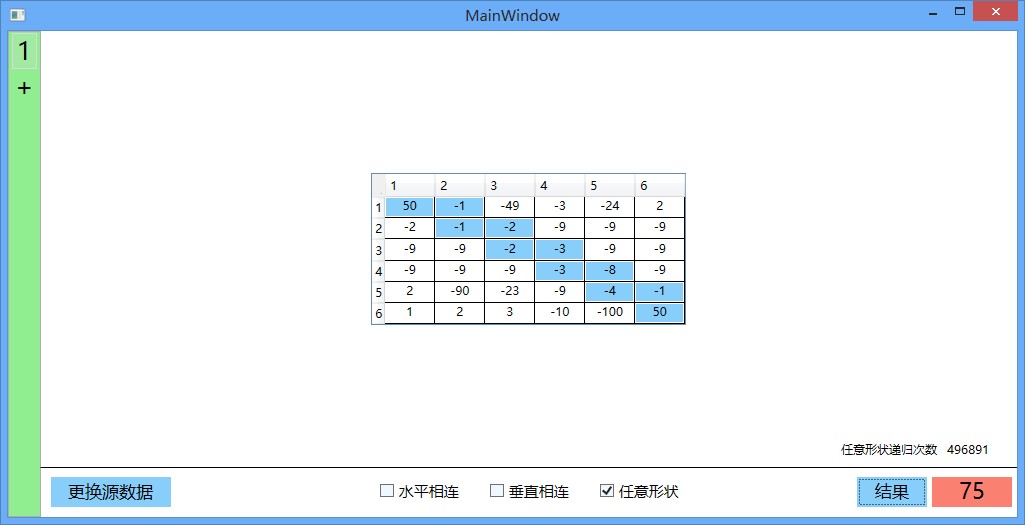

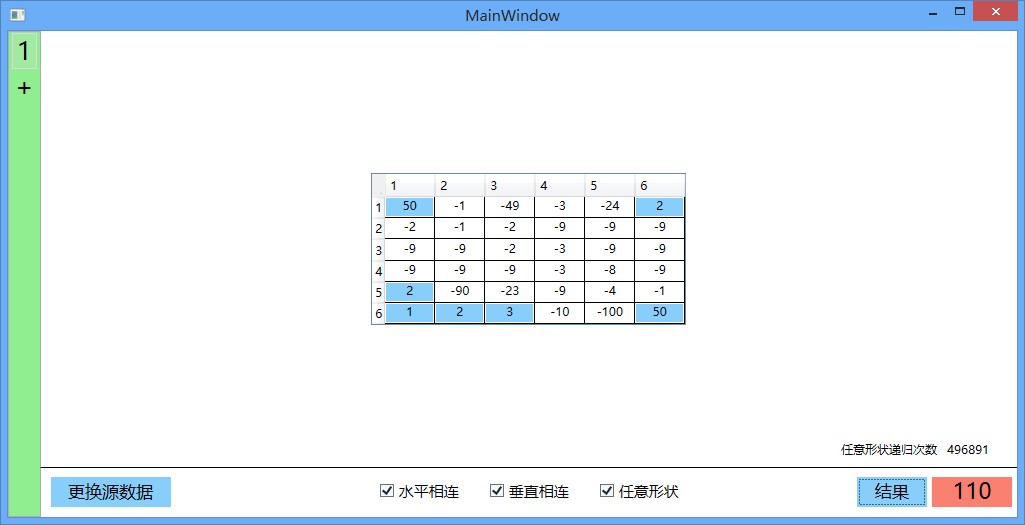
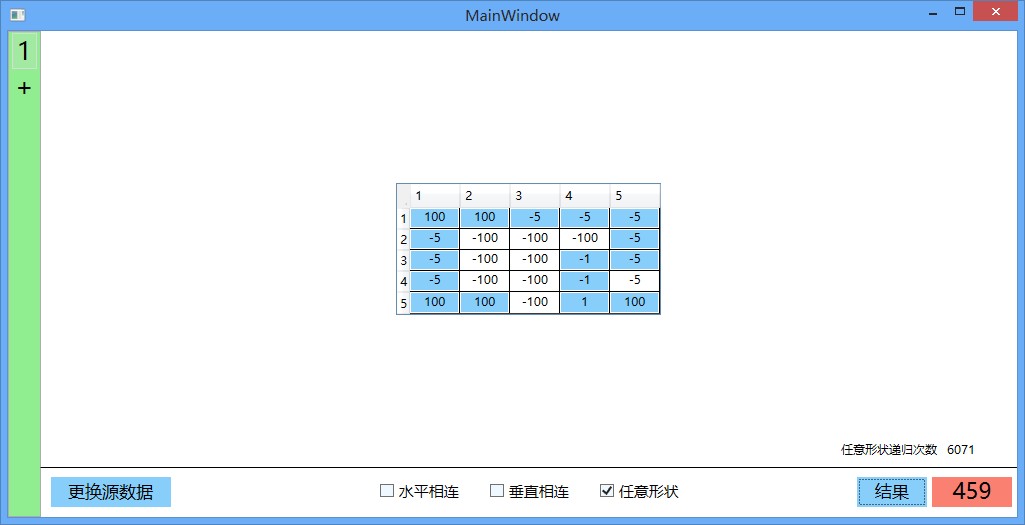

【现代程序设计】【homework-03】【11061027】的更多相关文章
- nlp homework 03
NLP Homework 03 --冯煜博 题目描述 (盒子和球模型)假设有3个盒子,每个盒子里装有红白两种颜色的球,盒子里的红白球有下表列出,初始状态分布. 解答 1. 给出HMM模型 \(\mu= ...
- 标准C程序设计七---03
Linux应用 编程深入 语言编程 标准C程序设计七---经典C11程序设计 以下内容为阅读: <标准C程序设计>(第7版) 作者 ...
- 现代程序设计homework——04
题目: 详见:http://www.cnblogs.com/xinz/p/3341551.html 题目本身确实很难,“很难想到一个比较优雅的算法”,这是一个老师请来专门讲解这道题的大牛的原话.确实, ...
- 小兔JS教程(四)-- 彻底攻略JS数组
在开始本章之前,先给出上一节的答案,参考答案地址: http://www.xiaotublog.com/demo.html?path=homework/03/index2 1.JS数组的三大特性 在J ...
- 小兔JS教程(三)-- 彻底攻略JS回调函数
这一讲来谈谈回调函数. 其实一句话就能概括这个东西: 回调函数就是把一个函数当做参数,传入另一个函数中.传进去的目的仅仅是为了在某个时刻去执行它. 如果不执行,那么你传一个函数进去干嘛呢? 就比如说对 ...
- vs2015c++/MFC入门知识全集/实例规范书籍视频下载孙鑫c++对话框计算器基础控件使用教程系列
VIP教程可免费看.可免费下载前部分试看教程地址:http://dwz.cn/4PcfPk免费下载地址:http://dwz.cn/mfc888 本课程目录 67章 [MFC项目开发第01天]Wind ...
- 软工+C(9): 助教指南,持续更新...
上一篇:提问与回复 下一篇:从命令行开始逐步培养编程能力(Java) 目录: ** 0x00 Handshake ** 0x01 点评 ** 0x02 评分 ** 0x03 知识储备 ** 0x04 ...
- 分享一套C++入门基础视频
本课程从C++起步.用户无需不论什么计算机基础,仅仅须要懂的主要的电脑操作,既可学习本课程.本课程适合在校大学生,在职人员等,通过本课程的学习,学员可掌握C++\MFC\VC++server端.网络编 ...
- 20172319 2018.03.27-04.05 《Java程序设计》第4周学习总结
20172319 2018.03.27-04.05 <Java程序设计>第4周学习总结 教材学习内容总结 第四章 编写类 类与对象的回顾:对象是有状态的,状态由对象的属性值确定.属性由类中 ...
- 20145219 《Java程序设计》第03周学习总结
20145219 <Java程序设计>第03周学习总结 教材学习内容总结 基本类型和类类型 基本类型:第三章中讲述的那几种,short.long.int.byte.double.char. ...
随机推荐
- [Ruby on Rails系列]5、专题:Talk About SaSS
This is my presentation in the Rails lecture of Hosei University. I will introduce SaSS by 5 example ...
- UPDATE和SELECT嵌套使用
1 2 update a set HIGH=b.NEW from SPEC1 a,tmpDOT b where a.high=b.old
- node.js模块之Buffer模块
http://nodejs.org/api/buffer.html Pure JavaScript is Unicode friendly but not nice to binary data. W ...
- HTML5 JS API 本地存储LocalStorage基本操作
LocalStorage:使用方法与SessionStorage如出一辙,如下代码所示:此对象主要有两个方法:保存数据:localStorage.setItem(Key, value);读取数据:lo ...
- VPN DNS leak 问题的解决
前一段时间遇到一个问题.customer说发现连接VPN后在PPP端发现security leak,整个转了好大一个圈子才把问题解决了.之所以费这么大周折,倒不是因为很难解决,只是费了很大劲儿才定位了 ...
- Task-based Asynchronous Pattern (TAP)
The Task-based Asynchronous Pattern (TAP) is based on the System.Threading.Tasks.Task and System.Thr ...
- Android开发之ContentValues
SQLite数据库进行CRUD的时候, 用到了ContentValues类,负责存储名值对,名都是String类型,值都是基本类型. 例子: ContentValues values=new Cont ...
- WPF中映射clr namspace
1. xaml中直接映射为prefix xmlns:prefix="clr-namespace:MyApplication.Modules.Entity;assembly=MyAssembl ...
- UVA 1658 Admiral 海上将军(最小费用流,拆点)
题意: 一个有v个点的有向图,要从点1到点v需要找两条路径,两路径不可经过同一个点(除了1和v点).求这两条路径的最小费用(保证有解). 分析: 难在建图,其他套模板. 此图给的是超级复杂图,两个点之 ...
- JDK版本1.6和6.0到底指什么
Both version numbers (1.6.0 and 6) are used to identify this release of the Java Platform. Version 6 ...
