增强学习(Reinforcement Learning and Control)
增强学习(Reinforcement Learning and Control)
[pdf版本]增强学习.pdf在之前的讨论中,我们总是给定一个样本x,然后给或者不给label y。之后对样本进行拟合、分类、聚类或者降维等操作。然而对于很多序列决策或者控制问题,很难有这么规则的样本。比如,四足机器人的控制问题,刚开始都不知道应该让其动那条腿,在移动过程中,也不知道怎么让机器人自动找到合适的前进方向。
另外如要设计一个下象棋的AI,每走一步实际上也是一个决策过程,虽然对于简单的棋有A*的启发式方法,但在局势复杂时,仍然要让机器向后面多考虑几步后才能决定走哪一步比较好,因此需要更好的决策方法。
对于这种控制决策问题,有这么一种解决思路。我们设计一个回报函数(reward function),如果learning agent(如上面的四足机器人、象棋AI程序)在决定一步后,获得了较好的结果,那么我们给agent一些回报(比如回报函数结果为正),得到较差的结果,那么回报函数为负。比如,四足机器人,如果他向前走了一步(接近目标),那么回报函数为正,后退为负。如果我们能够对每一步进行评价,得到相应的回报函数,那么就好办了,我们只需要找到一条回报值最大的路径(每步的回报之和最大),就认为是最佳的路径。
增强学习在很多领域已经获得成功应用,比如自动直升机,机器人控制,手机网络路由,市场决策,工业控制,高效网页索引等。
接下来,先介绍一下马尔科夫决策过程(MDP,Markov decision processes)。
1. 马尔科夫决策过程
一个马尔科夫决策过程由一个五元组构成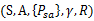
* S表示状态集(states)。(比如,在自动直升机系统中,直升机当前位置坐标组成状态集)
* A表示一组动作(actions)。(比如,使用控制杆操纵的直升机飞行方向,让其向前,向后等)
* 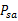 是状态转移概率。S中的一个状态到另一个状态的转变,需要A来参与。
是状态转移概率。S中的一个状态到另一个状态的转变,需要A来参与。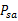 表示的是在当前
表示的是在当前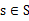 状态下,经过
状态下,经过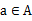 作用后,会转移到的其他状态的概率分布情况(当前状态执行a后可能跳转到很多状态)。
作用后,会转移到的其他状态的概率分布情况(当前状态执行a后可能跳转到很多状态)。
* 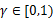 是阻尼系数(discount factor)
是阻尼系数(discount factor)
* 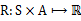 ,R是回报函数(reward function),回报函数经常写作S的函数(只与S有关),这样的话,R重新写作
,R是回报函数(reward function),回报函数经常写作S的函数(只与S有关),这样的话,R重新写作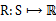 。
。
MDP的动态过程如下:某个agent的初始状态为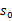 ,然后从A中挑选一个动作
,然后从A中挑选一个动作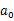 执行,执行后,agent按
执行,执行后,agent按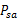 概率随机转移到了下一个
概率随机转移到了下一个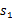 状态,
状态,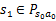 。然后再执行一个动作
。然后再执行一个动作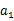 ,就转移到了
,就转移到了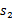 ,接下来再执行
,接下来再执行 …,我们可以用下面的图表示整个过程
…,我们可以用下面的图表示整个过程
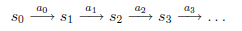
如果对HMM有了解的话,理解起来比较轻松。
我们定义经过上面转移路径后,得到的回报函数之和如下
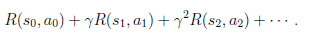
如果R只和S有关,那么上式可以写作
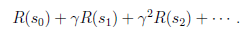
我们的目标是选择一组最佳的action,使得全部的回报加权和期望最大。
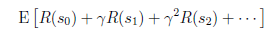
从上式可以发现,在t时刻的回报值被打了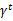 的折扣,是一个逐步衰减的过程,越靠后的状态对回报和影响越小。最大化期望值也就是要将大的
的折扣,是一个逐步衰减的过程,越靠后的状态对回报和影响越小。最大化期望值也就是要将大的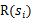 尽量放到前面,小的尽量放到后面。
尽量放到前面,小的尽量放到后面。
已经处于某个状态s时,我们会以一定策略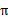 来选择下一个动作a执行,然后转换到另一个状态s’。我们将这个动作的选择过程称为策略(policy),每一个policy其实就是一个状态到动作的映射函数
来选择下一个动作a执行,然后转换到另一个状态s’。我们将这个动作的选择过程称为策略(policy),每一个policy其实就是一个状态到动作的映射函数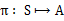 。给定
。给定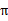 也就给定了
也就给定了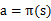 ,也就是说,知道了
,也就是说,知道了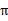 就知道了每个状态下一步应该执行的动作。
就知道了每个状态下一步应该执行的动作。
我们为了区分不同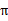 的好坏,并定义在当前状态下,执行某个策略
的好坏,并定义在当前状态下,执行某个策略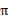 后,出现的结果的好坏,需要定义值函数(value function)也叫折算累积回报(discounted cumulative reward)
后,出现的结果的好坏,需要定义值函数(value function)也叫折算累积回报(discounted cumulative reward)
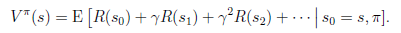
可以看到,在当前状态s下,选择好policy后,值函数是回报加权和期望。这个其实很容易理解,给定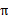 也就给定了一条未来的行动方案,这个行动方案会经过一个个的状态,而到达每个状态都会有一定回报值,距离当前状态越近的其他状态对方案的影响越大,权重越高。这和下象棋差不多,在当前棋局
也就给定了一条未来的行动方案,这个行动方案会经过一个个的状态,而到达每个状态都会有一定回报值,距离当前状态越近的其他状态对方案的影响越大,权重越高。这和下象棋差不多,在当前棋局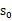 下,不同的走子方案是
下,不同的走子方案是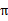 ,我们评价每个方案依靠对未来局势(
,我们评价每个方案依靠对未来局势(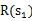 ,
,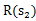 ,…)的判断。一般情况下,我们会在头脑中多考虑几步,但是我们会更看重下一步的局势。
,…)的判断。一般情况下,我们会在头脑中多考虑几步,但是我们会更看重下一步的局势。
从递推的角度上考虑,当期状态s的值函数V,其实可以看作是当前状态的回报R(s)和下一状态的值函数V’之和,也就是将上式变为:
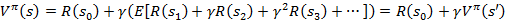
然而,我们需要注意的是虽然给定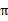 后,在给定状态s下,a是唯一的,但
后,在给定状态s下,a是唯一的,但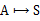 可能不是多到一的映射。比如你选择a为向前投掷一个骰子,那么下一个状态可能有6种。再由Bellman等式,从上式得到
可能不是多到一的映射。比如你选择a为向前投掷一个骰子,那么下一个状态可能有6种。再由Bellman等式,从上式得到
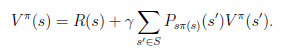
s’表示下一个状态。
前面的R(s)称为立即回报(immediate reward),就是R(当前状态)。第二项也可以写作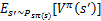 ,是下一状态值函数的期望值,下一状态s’符合
,是下一状态值函数的期望值,下一状态s’符合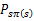 分布。
分布。
可以想象,当状态个数有限时,我们可以通过上式来求出每一个s的V(终结状态没有第二项V(s’))。如果列出线性方程组的话,也就是|S|个方程,|S|个未知数,直接求解即可。
当然,我们求V的目的就是想找到一个当前状态s下,最优的行动策略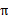 ,定义最优的V*如下:
,定义最优的V*如下:
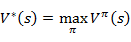
就是从可选的策略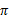 中挑选一个最优的策略(discounted rewards最大)。
中挑选一个最优的策略(discounted rewards最大)。
上式的Bellman等式形式如下:
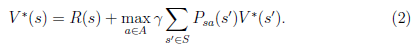
第一项与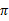 无关,所以不变。第二项是一个
无关,所以不变。第二项是一个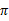 就决定了每个状态s的下一步动作a,执行a后,s’按概率分布的回报概率和的期望。
就决定了每个状态s的下一步动作a,执行a后,s’按概率分布的回报概率和的期望。
如果上式还不好理解的话,可以参考下图:
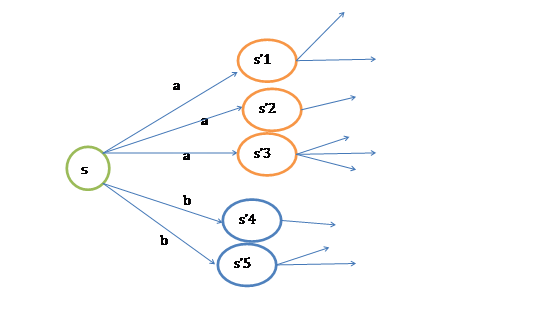
定义了最优的V*,我们再定义最优的策略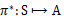 如下:
如下:
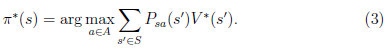
选择最优的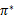 ,也就确定了每个状态s的下一步最优动作a。
,也就确定了每个状态s的下一步最优动作a。
根据以上式子,我们可以知道
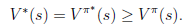
解释一下就是当前状态的最优的值函数V*,是由采用最优执行策略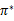 的情况下得出的,采用最优执行方案的回报显然要比采用其他的执行策略
的情况下得出的,采用最优执行方案的回报显然要比采用其他的执行策略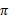 要好。
要好。
这里需要注意的是,如果我们能够求得每个s下最优的a,那么从全局来看,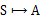 的映射即可生成,而生成的这个映射是最优映射,称为
的映射即可生成,而生成的这个映射是最优映射,称为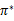 。
。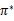 针对全局的s,确定了每一个s的下一个行动a,不会因为初始状态s选取的不同而不同。
针对全局的s,确定了每一个s的下一个行动a,不会因为初始状态s选取的不同而不同。
2. 值迭代和策略迭代法
上节我们给出了迭代公式和优化目标,这节讨论两种求解有限状态MDP具体策略的有效算法。这里,我们只针对MDP是有限状态、有限动作的情况,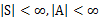 。
。
* 值迭代法
|
1、 将每一个s的V(s)初始化为0 2、 循环直到收敛 { 对于每一个状态s,对V(s)做更新
} |
值迭代策略利用了上节中公式(2)
内循环的实现有两种策略:
1、 同步迭代法
拿初始化后的第一次迭代来说吧,初始状态所有的V(s)都为0。然后对所有的s都计算新的V(s)=R(s)+0=R(s)。在计算每一个状态时,得到新的V(s)后,先存下来,不立即更新。待所有的s的新值V(s)都计算完毕后,再统一更新。
这样,第一次迭代后,V(s)=R(s)。
2、 异步迭代法
与同步迭代对应的就是异步迭代了,对每一个状态s,得到新的V(s)后,不存储,直接更新。这样,第一次迭代后,大部分V(s)>R(s)。
不管使用这两种的哪一种,最终V(s)会收敛到V*(s)。知道了V*后,我们再使用公式(3)来求出相应的最优策略 ,当然
,当然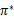 可以在求V*的过程中求出。
可以在求V*的过程中求出。
* 策略迭代法
值迭代法使V值收敛到V*,而策略迭代法关注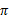 ,使
,使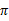 收敛到
收敛到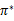 。
。
|
1、 将随机指定一个S到A的映射 2、 循环直到收敛 { (a) 令 (b) 对于每一个状态s,对
} |
(a)步中的V可以通过之前的Bellman等式求得
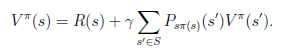
这一步会求出所有状态s的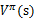 。
。
(b)步实际上就是根据(a)步的结果挑选出当前状态s下,最优的a,然后对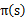 做更新。
做更新。
对于值迭代和策略迭代很难说哪种方法好,哪种不好。对于规模比较小的MDP来说,策略一般能够更快地收敛。但是对于规模很大(状态很多)的MDP来说,值迭代比较容易(不用求线性方程组)。
3. MDP中的参数估计
在之前讨论的MDP中,我们是已知状态转移概率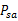 和回报函数R(s)的。但在很多实际问题中,这些参数不能显式得到,我们需要从数据中估计出这些参数(通常S、A和
和回报函数R(s)的。但在很多实际问题中,这些参数不能显式得到,我们需要从数据中估计出这些参数(通常S、A和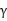 是已知的)。
是已知的)。
假设我们已知很多条状态转移路径如下:
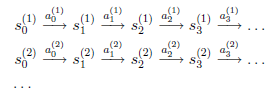
其中,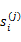 是i时刻,第j条转移路径对应的状态,
是i时刻,第j条转移路径对应的状态,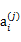 是
是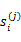 状态时要执行的动作。每个转移路径中状态数是有限的,在实际操作过程中,每个转移链要么进入终结状态,要么达到规定的步数就会终结。
状态时要执行的动作。每个转移路径中状态数是有限的,在实际操作过程中,每个转移链要么进入终结状态,要么达到规定的步数就会终结。
如果我们获得了很多上面类似的转移链(相当于有了样本),那么我们就可以使用最大似然估计来估计状态转移概率。

分子是从s状态执行动作a后到达s’的次数,分母是在状态s时,执行a的次数。两者相除就是在s状态下执行a后,会转移到s’的概率。
为了避免分母为0的情况,我们需要做平滑。如果分母为0,则令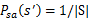 ,也就是说当样本中没有出现过在s状态下执行a的样例时,我们认为转移概率均分。
,也就是说当样本中没有出现过在s状态下执行a的样例时,我们认为转移概率均分。
上面这种估计方法是从历史数据中估计,这个公式同样适用于在线更新。比如我们新得到了一些转移路径,那么对上面的公式进行分子分母的修正(加上新得到的count)即可。修正过后,转移概率有所改变,按照改变后的概率,可能出现更多的新的转移路径,这样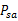 会越来越准。
会越来越准。
同样,如果回报函数未知,那么我们认为R(s)为在s状态下已经观测到的回报均值。
当转移概率和回报函数估计出之后,我们可以使用值迭代或者策略迭代来解决MDP问题。比如,我们将参数估计和值迭代结合起来(在不知道状态转移概率情况下)的流程如下:
|
1、 随机初始化 2、 循环直到收敛 { (a) 在样本上统计 (b) 使用估计到的参数来更新V(使用上节的值迭代方法) (c) 根据更新的V来重新得出 } |
在(b)步中我们要做值更新,也是一个循环迭代的过程,在上节中,我们通过将V初始化为0,然后进行迭代来求解V。嵌套到上面的过程后,如果每次初始化V为0,然后迭代更新,就会很慢。一个加快速度的方法是每次将V初始化为上一次大循环中得到的V。也就是说V的初值衔接了上次的结果。
4. 总结
首先我们这里讨论的MDP是非确定的马尔科夫决策过程,也就是回报函数和动作转换函数是有概率的。在状态s下,采取动作a后的转移到的下一状态s’也是有概率的。再次,在增强学习里有一个重要的概念是Q学习,本质是将与状态s有关的V(s)转换为与a有关的Q。强烈推荐Tom Mitchell的《机器学习》最后一章,里面介绍了Q学习和更多的内容。最后,里面提到了Bellman等式,在《算法导论》中有Bellman-Ford的动态规划算法,可以用来求解带负权重的图的最短路径,里面最值得探讨的是收敛性的证明,非常有价值。有学者仔细分析了增强学习和动态规划的关系。
这篇是ng讲义中最后一篇了,还差一篇learning theory,暂时不打算写了,感觉对learning的认识还不深。等到学习完图模型和在线学习等内容后,再回过头来写learning theory吧。另外,ng的讲义中还有一些数学基础方面的讲义比如概率论、线性代数、凸优化、高斯过程、HMM等,都值得看一下。
增强学习(Reinforcement Learning and Control)的更多相关文章
- 增强学习Reinforcement Learning经典算法梳理3:TD方法
转自:http://blog.csdn.net/songrotek/article/details/51382759 博客地址:http://blog.csdn.net/songrotek/artic ...
- 深度学习国外课程资料(Deep Learning for Self-Driving Cars)+(Deep Reinforcement Learning and Control )
MIT(Deep Learning for Self-Driving Cars) CMU(Deep Reinforcement Learning and Control ) 参考网址: 1 Deep ...
- [Reinforcement Learning] Model-Free Control
上篇总结了 Model-Free Predict 问题及方法,本文内容介绍 Model-Free Control 方法,即 "Optimise the value function of a ...
- 强化学习(Reinforcement Learning)中的Q-Learning、DQN,面试看这篇就够了!
1. 什么是强化学习 其他许多机器学习算法中学习器都是学得怎样做,而强化学习(Reinforcement Learning, RL)是在尝试的过程中学习到在特定的情境下选择哪种行动可以得到最大的回报. ...
- 强化学习 reinforcement learning: An Introduction 第一章, tic-and-toc 代码示例 (结构重建版,注释版)
强化学习入门最经典的数据估计就是那个大名鼎鼎的 reinforcement learning: An Introduction 了, 最近在看这本书,第一章中给出了一个例子用来说明什么是强化学习, ...
- Andrew Ng机器学习公开课笔记–Reinforcement Learning and Control
网易公开课,第16课 notes,12 前面的supervised learning,对于一个指定的x可以明确告诉你,正确的y是什么 但某些sequential decision making问题,比 ...
- 论文笔记之:Active Object Localization with Deep Reinforcement Learning
Active Object Localization with Deep Reinforcement Learning ICCV 2015 最近Deep Reinforcement Learning算 ...
- Deep Reinforcement Learning 基础知识
Introduction 深度增强学习Deep Reinforcement Learning是将深度学习与增强学习结合起来从而实现从Perception感知到Action动作的端对端学习的一种全新的算 ...
- Deep Reinforcement Learning 基础知识(DQN方面)
Introduction 深度增强学习Deep Reinforcement Learning是将深度学习与增强学习结合起来从而实现从Perception感知到Action动作的端对端学习的一种全新的算 ...
随机推荐
- 使用SQLite3持久保存应用程序数据
前言 SQL是一种数据库查询语言,用于存取数据以及查询.更新和管理关系数据库系统,因为强大的查询功能和简单的语法,已经成为主流数据库的标准语言.SQLite3是一种嵌入式的数据库,无需服务器支持,它将 ...
- Xcode中如何更改Bundle identifier
1.如图所示,更改Info.plist 中的Bundle identifier
- Tomcat 优化 java.lang.OutOfMemoryError: Java heap space 的解决方法
Tomcat 优化 java.lang.OutOfMemoryError: Java heap space 的解决方法 java.lang.OutOfMemoryError: Java heap sp ...
- Netfilter深度解剖
在网络上发现这个Netfilter写的很好的系列文章,为了便于后期寻找,特此标注下博客地址,感谢大大神提供. ---------------------------分割线开始---- ...
- C++使用类型代替枚举量
自己写的C++类型枚举量,可以使用类型识别取代模板,绑定枚举量和多组调用函数,在调用阶段只要指定某组函数就可以根据枚举量调用相应函数. 代码如下: #ifndef __MYENUM_H__ #defi ...
- ASP.Net网站部署失败
部署站点时候,出现如下错误 “/”应用程序中的服务器错误. ---------------------------------------------------------------------- ...
- TOMCAT内存大小调整
Tomcat本身不能直接在计算机上运行,需要依赖于硬件基础之上的操作系统和一个java虚拟机.JAVA程序启动时JVM都会分配一个初始内存和最大内存给这个应用程序.这个初始内存和最大内存在一定程度都会 ...
- Flash Activex NPAPI PPAPI 各种网页插件完整安装包下载地址
内容全部是自己手工原创写作的参考内容,完全排除从其他网站COPY的内容信息.如有雷同实属巧合. 奉献给有需求的人士,也给各位解决FLASH安装头疼的问题,正常在线下载安装运气不好的安装半天.运气好 ...
- How to disable Passwords must meet complexity requirements[windows 7]
The Password complexity is a Local Policy setting named "Passwords must meet complexity require ...
- Jquery LigerUI框架学习(二)之Tree于Tab标签实现iframe功能
LigerUI框架Tree于Tab标签动态使用,当点击Tree后动态创建Tab标签,和通常用的iframe框架功能类似 Tree中的关键代码 //Tree初始化 $("#tree1" ...


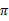 。
。
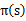 做更新
做更新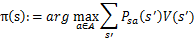
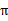
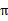 中每个状态转移次数,用来更新
中每个状态转移次数,用来更新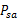 和R
和R