BM25相关度打分公式

BM25算法是一种常见用来做相关度打分的公式，思路比较简单，主要就是计算一个query里面所有词和文档的相关度，然后在把分数做累加操作,而每个词的相关度分数主要还是受到tf/idf的影响。公式如下：

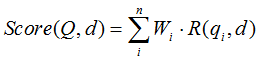
R(qi,d)是每个词和文档的相关度值，其中qi代表每个词，d代表相关的文档，Wi是这个词的权重，然后所有词的乘积再做累加。

Wi可由外部设置，默认的话是idf值，公式如下，N是文档总数，n(qi)是包含该词的文档数，0.5是调教系数，避免n(qi)为0的情况，从这个公式可以看出N越大，n(qi)越小的花idf值越大，这也符合了"词的重要程度和其出现在总文档集合里的频率成反比"的思想，取个log是为了让idf的值受N和n(qi)的影响更加平滑。

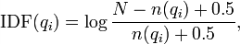
下面是R(qi,d)的公式，其中k1，k2，b都是调节因子，一般k1=2，k2=1，b=0.75,fi是词在文档中的次数，qfi代表词在查询语句里的次数，dl是文档长度，avgdl是文档平均长度，可以看出如果其他因素一样dl越大，相关度越低，这个也符合结论，至于会除以一个avgdl，我想是拿本篇文档长度和整体文档长度水平做比较 ，以免单独取dl值时过大。

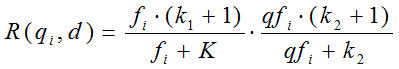
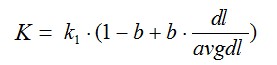
其中乘积的左边因数代表词在文档中的次数关系，乘积的右边因数代表词在查询语句中的次数关系，一般绝大多数情况，查询词在查询语句里面出现一次，所以qfi可以看成是1，又因为k2为1，所以右边因数其实就等于1，所以公式可化简为下面这样

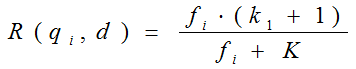
而总公式化简后可得

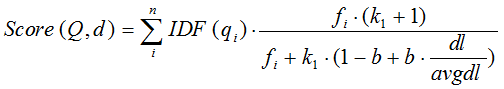
影响BM25公式的因数有

1 idf，idf越高分数越高

2 tf tf越高分数越高

3 dl/avgdl 如果该文档长度在文档水平中越高则分数越低。

4 k1，b为分数的调节因子