利用Minhash和LSH寻找相似的集合（转）

问题背景

给出N个集合，找到相似的集合对，如何实现呢？直观的方法是比较任意两个集合。那么可以十分精确的找到每一对相似的集合，但是时间复杂度是O(n²)。当N比较小时，比如K级，此算法可以在接受的时间范围内完成，但是如果N变大时，比B级，甚至P级，那么需要的时间是不能够被接受的。比如N= 1B = 1,000,000,000。一台计算机每秒可以比较1,000,000,000对集合是否相等。那么大概需要15年的时间才能找到所有相似的集合！

上面的算法虽然效率很低，但是结果会很精确，因为检查了每一对集合。假如，N个集合中只有少数几对集合相似，绝大多数集合都不等呢？那么根据上述算法，绝大多数检测的结果是两个结合不相似，可以说这些检测“浪费了计算时间”。所以，如果能找到一种算法，将大体上相似的集合聚到一起，缩小比对的范围，这样只用检测较少的集合对，就可以找到绝大多数相似的集合对，大幅度减少时间开销。虽然牺牲了一部分精度，但是如果能够将时间大幅度减少，这种算法还是可以接受的。接下来的内容讲解如何使用Minhash和LSH（Locality-sensitive Hashing）来实现上述目的，在相似的集合较少的情况下，可以在O(n)时间找到大部分相似的集合对。

Jaccard相似度

判断两个集合是否相等，一般使用称之为Jaccard相似度的算法（后面用Jac(S₁,S₂)来表示集合S₁和S₂的Jaccard相似度）。举个列子，集合X = {a,b,c}，Y = {b,c,d}。那么Jac(X,Y) = 2 / 3 = 0.67。也就是说，结合X和Y有67%的元素相同。下面是形式的表述Jaccard相似度公式：

Jac(X,Y) = |X∩Y| / |X∪Y|

也就是两个结合交集的个数比上两个集合并集的个数。范围在[0,1]之间。

降维技术Minhash

原始问题的关键在于计算时间太长。所以，如果能够找到一种很好的方法将原始集合压缩成更小的集合，而且又不失去相似性，那么可以缩短计算时间。Minhash可以帮助我们解决这个问题。举个例子，S₁ = {a,d,e}，S₂ = {c, e}，设全集U = {a,b,c,d,e}。集合可以如下表示：

行号	元素	S1	S2	类别
1	a	1	0	Y
2	b	0	0	Z
3	c	0	1	Y
4	d	1	0	Y
5	e	1	1	X

表1

表1中，列表示集合，行表示元素，值1表示某个集合具有某个值，0则相反（X，Y，Z的意义后面讨论）。Minhash算法大体思路是：采用一种hash函数，将元素的位置均匀打乱，然后将新顺序下每个集合第一个元素作为该集合的特征值。比如哈希函数h₁(i) = (i + 1) % 5，其中i为行号。作用于集合S₁和S₂，得到如下结果：

行号	元素	S1	S2	类别
1	e	1	1	X
2	a	1	0	Y
3	b	0	0	Z
4	c	0	1	Y
5	d	1	0	Y
Minhash		e	e

表2

这时，Minhash(S₁) = e，Minhash(S₂) = e。也就是说用元素e表示S₁，用元素e表示集合S₂。那么这样做是否科学呢？进一步，如果Minhash(S₁) 等于Minhash(S₂)，那么S₁是否和S₂类似呢？

一个神奇的结论

P(Minhash(S­₁) = Minhash(S₂)) = Jac(S₁,S₂)

在哈希函数h₁均匀分布的情况下，集合S₁的Minhash值和集合S₂的Minhash值相等的概率等于集合S₁与集合S₂的Jaccard相似度，下面简单分析一下这个结论。

S₁和S₂的每一行元素可以分为三类：

l  X类 均为1。比如表2中的第1行，两个集合都有元素e。

l  Y类 一个为1，另一个为0。比如表2中的第2行，表明S₁有元素a，而S₂没有。

l  Z类 均为0。比如表2中的第3行，两个集合都没有元素b。

这里忽略所有Z类的行，因为此类行对两个集合是否相似没有任何贡献。由于哈希函数将原始行号均匀分布到新的行号，这样可以认为在新的行号排列下，任意一行出现X类的情况的概率为|X|/(|X|+|Y|)。这里为了方便，将任意位置设为第一个出现X类行的行号。所以P(第一个出现X类) = |X|/(|X|+|Y|) = Jac(S₁,S₂)。这里很重要的一点就是要保证哈希函数可以将数值均匀分布，尽量减少冲撞。

一般而言，会找出一系列的哈希函数，比如h个（h << |U|），为每一个集合计算h次Minhash值，然后用h个Minhash值组成一个摘要来表示当前集合（注意Minhash的值的位置需要保持一致）。举个列子，还是基于上面的例子，现在又有一个哈希函数h₂(i) = (i -1)% 5。那么得到如下集合：

行号	元素	S1	S2	类别
1	b	0	0	Z
2	c	0	1	Y
3	d	1	0	Y
4	e	1	1	X
5	a	1	0	Y
Minhash		d	c

表3

所以，现在用摘要表示的原始集合如下：

哈希函数	S1	S2
h1(i) = (i + 1) % 5	e	e
h2(i) = (i - 1) % 5	d	c

表4

从表四还可以得到一个结论，令X表示Minhash摘要后的集合对应行相等的次数（比如表4，X=1，因为哈希函数h₁情况下，两个集合的minhash相等，h₂不等）：

X ~ B(h,Jac(S₁,S₂))

X符合次数为h，概率为Jac(S₁,S₂)的二项分布。那么期望E(X) = h * Jac(S₁,S₂) = 2 * 2 / 3 = 1.33。也就是每2个hash计算Minhash摘要，可以期望有1.33元素对应相等。

所以，Minhash在压缩原始集合的情况下，保证了集合的相似度没有被破坏。

LSH – 局部敏感哈希

现在有了原始集合的摘要，但是还是没有解决最初的问题，仍然需要遍历所有的集合对,，才能所有相似的集合对，复杂度仍然是O(n²)。所以，接下来描述解决这个问题的核心思想LSH。其基本思路是将相似的集合聚集到一起，减小查找范围，避免比较不相似的集合。仍然是从例子开始，现在有5个集合，计算出对应的Minhash摘要，如下：

	S1	S2	S3	S4	S5
区间1	b	b	a	b	a
	c	c	a	c	b
	d	b	a	d	c
区间2	a	e	b	e	d
	b	d	c	f	e
	e	a	d	g	a
区间3	d	c	a	h	b
	a	a	b	b	a
	d	e	a	b	e
区间4	d	a	a	c	b
	b	a	c	b	a
	d	e	a	b	e

表5

上面的集合摘要采用了12个不同的hash函数计算出来，然后分成了B = 4个区间。前面已经分析过，任意两个集合（S₁，S₂）对应的Minhash值相等的概率r = Jac(S₁，S₂)。先分析区间1，在这个区间内，P(集合S₁等于集合S₂) = r³。所以只要S­₁和S₂的Jaccard相似度越高，在区间1内越有可能完成全一致，反过来也一样。那么P(集合S₁不等于集合S₂) = 1 - r³。现在有4个区间，其他区间与第一个相同，所以P(4个区间上，集合S₁都不等于集合S₂) = (1 – r³)⁴。P(4个区间上，至少有一个区间，集合S₁等于集合S₂) = 1 - (1 – r³)⁴。这里的概率是一个r的函数，形状犹如一个S型，如下：

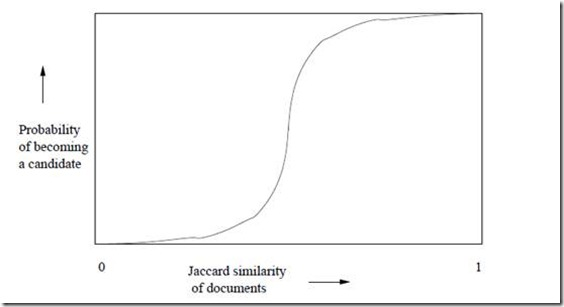
图1

如果令区间个数为B，每个区间内的行数为C，那么上面的公式可以形式的表示为：

P(B个区间中至少有一个区间中两个结合相等) = 1 - (1 – r^C)^B

领r = 0.4，C=3，B = 100。上述公式计算的概率为0.9986585。这表明两个Jaccard相似度为0.4的集合在至少一个区间内冲撞的概率达到了99.9%。根据这一事实，我们只需要选取合适的B和C，和一个冲撞率很低的hash函数，就可以将相似的集合至少在一个区间内冲撞，这样也就达成了本节最开始的目的：将相似的集合放到一起。具体的方法是为B个区间，准备B个hash表，和区间编号一一对应，然后用hash函数将每个区间的部分集合映射到对应hash表里。最后遍历所有的hash表，将冲撞的集合作为候选对象进行比较，找出相识的集合对。整个过程是采用O(n)的时间复杂度，因为B和C均是常量。由于聚到一起的集合相比于整体比较少，所以在这小范围内互相比较的时间开销也可以计算为常量，那么总体的计算时间也是O(n)。

总结

以上只是描述了Minhash和LSH寻找相似集合的算法框架，作为学习笔记和备忘录。还有一些算法细节没有讨论。希望后面有机会，可以在海量数据的情况下使用这个算法。