BZOJ 3809Gty的二逼妹子序列 解题报告+data marker

　　　　　　　　　　--BZOJ

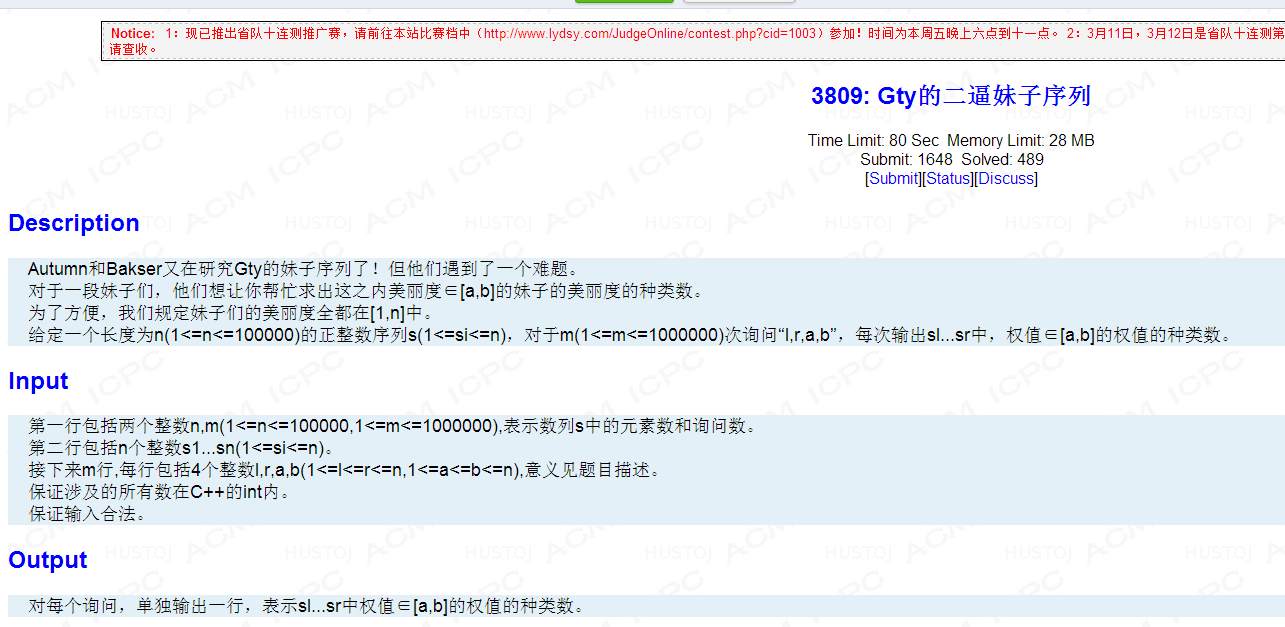
http://www.lydsy.com/JudgeOnline/problem.php?id=3809

---

---

考虑对l,r跑莫队，对一组维护美丽度出现次数的桶修改，

然后把桶序列用分块维护查询

然后是吐槽：

内存28M，哦，这个题居然卡内存。。。。。

卡内存！！！

然后我就为本校的权限号贡献了三次MLE......

代码：

 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 using std::sort;
 struct ss{
     int l,r,a,b,num;
 }x[];
 int n,m,cut;
 int tong[];
 int id[];
 int mark[];
 int a[];
 int ans[];
 bool cmp(ss a,ss b){
     if(id[a.l]==id[b.l])
         return a.r<b.r;
     return id[a.l]<id[b.l];
 }
 inline void in(int &ans)
 {
     ans=;bool p=false;char ch=getchar();
     while((ch>'' || ch<'')&&ch!='-') ch=getchar();
     if(ch=='-') p=true,ch=getchar();
     while(ch<=''&&ch>='') ans=ans*+ch-'',ch=getchar();
     if(p) ans=-ans;
 }
 void modui();
 int fin_brick(int l,int r);
 int main()
 {
     int i,j,k;
     in(n),in(m);
     cut=(int)sqrt(n);
     if(cut*cut<n)cut++;
     for(i=;i<=n;i++)
         in(a[i]);
     for(i=;i<=m;i++)
         in(x[i].l),in(x[i].r),in(x[i].a),in(x[i].b),x[i].num=i;
     for(i=;i<=n;i++)
         id[i]=i/cut;
     sort(x+,x+m+,cmp);
     modui();
     for(i=;i<=m;i++)
         printf("%d\n",ans[i]);
     return ;
 }
 void modui(){
     int l_p=x[].l,r_p=x[].l-,i;
     for(i=;i<=m;i++){
         while(r_p<x[i].r){
             r_p++;
             if(!tong[a[r_p]])
                 mark[a[r_p]/cut]++;
             tong[a[r_p]]++;
         }
         while(r_p>x[i].r){
             tong[a[r_p]]--;
             if(!tong[a[r_p]])
                 mark[a[r_p]/cut]--;
             r_p--;
         }
         while(l_p>x[i].l){
             l_p--;
             if(!tong[a[l_p]])
                 mark[a[l_p]/cut]++;
             tong[a[l_p]]++;
         }
         while(l_p<x[i].l){
             tong[a[l_p]]--;
             if(!tong[a[l_p]])
                 mark[a[l_p]/cut]--;
             l_p++;
         }
         ans[x[i].num]=fin_brick(x[i].a,x[i].b);
     }
 }
 int fin_brick(int l,int r){
     int b_l=l/cut,b_r=r/cut,ll=l%cut,rr=r%cut;
     int i,j,ans=;
     if(b_l==b_r){
         for(i=l;i<=r;i++)
             if(tong[i])
                 ans++;
         return ans;
     }
     for(i=ll,j=l;i<=cut-;i++,j++)
         if(tong[j])
             ans++;
     for(i=rr,j=r;i>=;i--,j--)
         if(tong[j])
             ans++;
     b_l++;b_r--;
     for(i=b_l;i<=b_r;i++)
         ans+=mark[i];
     return ans;
 }

#include<cstdio>
#include<cstdlib>
#include<ctime>
using namespace std;
int main()
{
    srand(time());
    int n=,m=;
    int i;
    printf("%d %d\n",n,m);
    for(i=;i<=n;i++)
        printf("%d ",rand()%n+);
    printf("\n");
    for(i=;i<=m;i++){
        int l=rand()%n+,a=rand()%n+;
        int r=l+rand()%(n-l+),b=a+rand()%(n-a+);
        printf("%d %d %d %d\n",l,r,a,b);
    }
}

data_maker

祝AC