C++语言实现-邻接矩阵

一、 图的概念

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（V，E），其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。在图中的数据元素，我们称之为顶点（Vertex），顶点集合有穷非空。在图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。在示意图中，我们使用点和圆来表示定点。

思考：只有若干顶点构成的图（不存在任何一条边）是不是上面所述的图？

二、名词解释

· 图按照边的有无方向分为无向图和有向图。无向图由顶点和边组成，有向图由顶点和弧构成。弧有弧尾和弧头之分，带箭头一端为弧头。

· 图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度。有向图顶点分为入度和出度。

· 图中顶点间存在路径，两顶点存在路径则说明是连通的；如果路径最终回到起始点则称为环。

无向图中连通且n个顶点n-1条边称为生成树。

三、图的存储结构之邻接矩阵

一个一维数组存储图中顶点信息；

一个二维数组（称为邻接矩阵）存储图中边或弧的信息。

1、 无向图：

　　　　　　　　　　

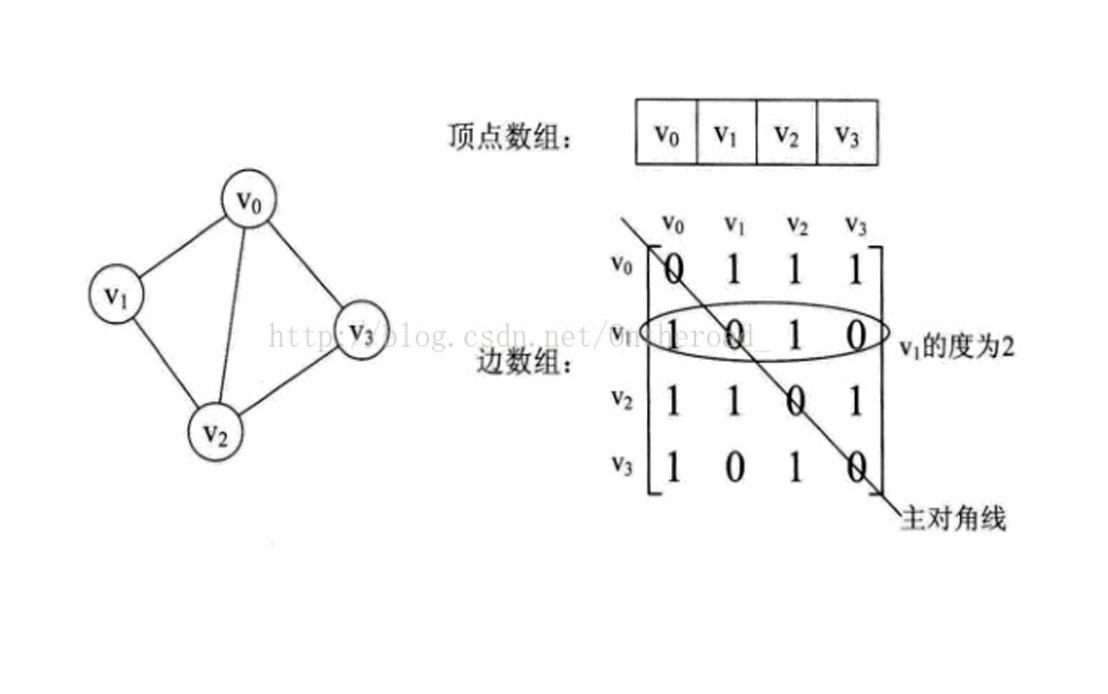
2、 有向图：

　　　　　　　　　　　　

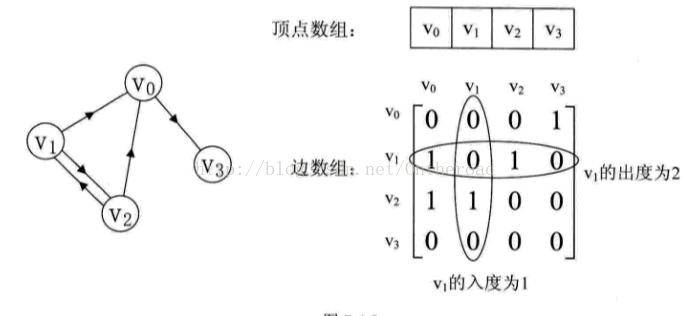
有向图的邻接矩阵实现

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int max_v=;

int main()
{
    int v,e;
    int x,y;//x->y
    int m[max_v][max_v];
    memset(m,,sizeof(m));
    cin>>v>>e;//输入顶点和边的个数
    for(int i=;i<e;i++)
    {
        cin>>x>>y;//输入每两个节点的的值表示两个节点之间的边的指向
        m[x][y]=;//存在有指向的边便赋值为1
    }
    for(int i=;i<v;i++)//输出邻接矩阵
    {
        for(int j=;j<v;j++)
            cout<<m[i][j]<<' ';
        cout<<endl;
    }
    return ;
}

输入：

5 12
1 0
0 1
1 2
2 1
0 3
3 0
3 4
4 3
1 3
3 1
2 3
3 2
输出结果：
0 1 0 1 0
1 0 1 1 0
0 1 0 1 0
1 1 1 0 1
0 0 0 1 0

此外，无向图的代码实现可参照有向图的实现方式