POJ - 2635 E - The Embarrassed Cryptographer

The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company.

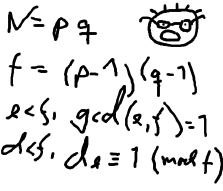
The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. 
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10 ¹⁰⁰ and 2 <= L <= 10 ⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10
143 20
667 20
667 30
2573 30
2573 40
0 0

Sample Output

GOOD
BAD 11
GOOD
BAD 23
GOOD
BAD 31

题意：求给出的一个数，求k中是否有比L小的的因子，其中K是大数

思路：因为我们L范围只有1e6，所以我们找寻因子可以直接遍历1-（L-1），然后我们进行大数取余操作，直接看余数是否为0即可
但是这样的时间复杂度就超时了，字符串长度是100  *  L范围1e6  *  20组数据  =  2*1e9  （超时）
这个时候我们就要进行优化20组数据我们无法优化，只能从大数取余和找因子这里入

1，找因子
我们可以只找素因子，如果素因子都不可以说明其他因子也行不通，所以我们可以进行素数筛法打表

2.大数取余
因为我们在进行找因子的时候我们每次都要进行大数取余，重复这个操作，我们就可以进行大数转换千进制，就可以在进行大数取余操作的时候大大缩减时间复杂度

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define MAX 1000100
using namespace std;
int n;
int prime[MAX+];
char str[];
void primetable()//素数打表
{
    int ps=;
    prime[ps++]=;
    for(int i=;i<=MAX;i+=)
    {
        int flag=;
        for(int j=;prime[j]*prime[j]<=i;j++)
        if(!(i%prime[j]))
        {
            flag=;
            break;
        }
        if(flag)
            prime[ps++]=i;
    }
}
int main()
{
    primetable();
    while(scanf("%s%d",str,&n)!=EOF)
    {
        if(str[]==''&&n==) break;
        int len=strlen(str);
        int ans=;
        int a[];
        for(int i=len-;i>=;)//转换成千进制
        {
            if(i<){
                if(i==)
                    a[ans++]=str[i]-'';
                else a[ans++]=str[i]-''+(str[i-]-'')*;
                i=-;
            }
            else{
                a[ans++]=str[i]-''+(str[i-]-'')*+(str[i-]-'')*;
                i-=;
            }
        }
        int flag=;
        for(int i=;prime[i]<n;i++)//遍历素因子
        {
            long long sum=;
            for(int j=ans-;j>=;j--)
            {
                sum=(sum*+a[j])%prime[i];
            }
            if(sum==)
            {
                printf("BAD %d\n",prime[i]);
                flag=;
                break;
            }
        }
        if(flag==)
        {
            printf("GOOD\n");
        }
    }
}