【做题】Codeforces Round #453 (Div. 1) D. Weighting a Tree——拆环

前言：结论题似乎是我的硬伤……

题意是给你一个无向图，已知连接到每一个点的边的权值和（为整数，且属于区间[-n,n]），需要求出每条边权值的一个合法解（都要是在区间[-2*n^2,2*n^2]内的整数）。

第一个想法当然是O(n^2*m)的高斯消元。在此基础上，我想过通过选取某些节点，在边权总和中减去与之相邻的边，来逐个解出边的权值。这个本质上是优化解方程的办法难以适应全部情况，且难以通过编程实现。于是只能舍弃这个想法。

后来通过漫无边际的瞎想，观察标题，容易发现对于一棵树求解这个问题是极为容易的。于是下一个思路就是把这个无向图转化为一棵树。如下图所示，偶环的情况是很容易就能解决的。（无脑删边）

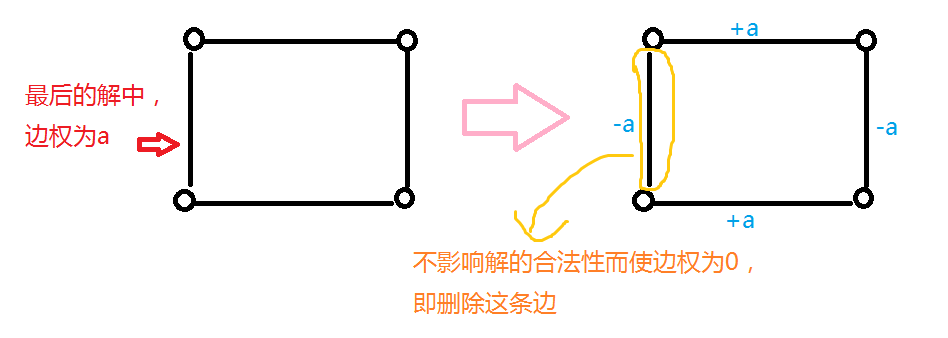
那么奇环怎么办呢？事实上，本人就卡在了这里。如果按照偶环的方法来解释奇环删边的合法性，我们发现最终有一个点的点权增加了2a。陷入僵局。这时，不妨让我们再考虑一下对树求解的过程。也就是一次dfs，对于除根结点之外的每一个结点都满足其权值和，再根据根结点是否满足其约束条件来判断是否有解。注意到上面奇环的操作，实质就意味着如果我们以一个奇环上的点为根结点，那么就可以在最后判断的时候任意加上一个偶数了。容易证明，最后与根结点相邻的边权和与其应有的边权和之差一定是一个偶数。也就是说，有奇环的图是一定有解的。因此，我们如上的处理奇环的方式，并不会影响解的存在性。

于是，我们就得到了处理环的方式：都不鸟它，并从奇环上随意拉一个点当根结点。

讲到这里，我们似乎还忽略了一个条件。

write a weight between  - 2·n² and 2·n² (inclusive) on each edge

当然，这个范围是相当大的，一般而言解是一定在这个区间内的（也仅限一般而言）。基于cf是一个有hack机制的网站，毫无疑问会有数据把你的解卡出这个区间（对本人而言是test 34）。因此，random_shuffle是必不可缺的。

时间复杂度O(n+m)。

 #include <bits/stdc++.h>
 #define int long long
 #define tag(i) (ed[((i)|1)>>1].id)
 using namespace std;
 const int N = ;
 struct edge {
     int la,b;
     edge(int la=,int b=):la(la),b(b) {};
 } con[N<<];
 int tot=,fir[N];
 void add(int from,int to) {
     con[++tot] = edge(fir[from],to);
     fir[from] = tot;
     con[++tot] = edge(fir[to],from);
     fir[to] = tot;
 }
 int c[N],ans[N],n,m,cnt,dep[N],rt,ano,fat[N],up[N],mar[N];
 typedef pair<int,int> pii;
 struct data {
     int a,b,id;
     data(int a=,int b=,int id=):a(a),b(b),id(id){}
 } ed[N];
 pii ext[N];
 bool vis[N];
 void dfs_init(int pos,int fa) {
     fat[pos] = fa;
     vis[pos] = ;
     dep[pos] = dep[fa] + ;
     for (int i = fir[pos] ; i ; i = con[i].la) {
         if (con[i].b == fa) continue;
         if (vis[con[i].b]) {
             if (pos > con[i].b) ext[++cnt] = pii(pos,i);
         } else dfs_init(con[i].b,pos),up[con[i].b] = tag(i);
     }
 }
 int dfs(int pos,int fa) {
     vis[pos] = ;
     int now = c[pos];
     for (int i = fir[pos] ; i ; i = con[i].la) {
         if (vis[con[i].b]) continue;
         now -= (ans[tag(i)] = dfs(con[i].b,pos));
     }
     return now;
 }
 bool ocy(pii x) {
     int a = x.first, b = con[x.second].b;
     return (dep[a] + dep[b] + )&;
 }
 void print() {
     puts("YES");
     for (int i =  ; i <= m ; ++ i) {
         cout << ans[i] << endl;
     }
 }
 void modify(int x,int y) {
     int k1 = , k2 = -;
     while (dep[x] > dep[y]) {
         mar[up[x]] += k1;
         k1 = -k1;
         x = fat[x];
     }
     while (dep[y] > dep[x]) {
         mar[up[y]] += k2;
         k2 = -k2;
         y = fat[y];
     }
     while (x != y) {
         mar[up[x]] += k1;
         k1 = -k1;
         x = fat[x];
         mar[up[y]] += k2;
         k2 = -k2;
         y = fat[y];
     }
 }
 signed main() {
     int a,b;
     cin >> n >> m;
     for (int i =  ; i <= n ; ++ i) cin>>c[i];
     for (int i =  ; i <= m ; ++ i) {
         cin >> a >> b;
         ed[i] = data(a,b,i);
     }
     random_shuffle(ed+,ed+m+);
     for (int i =  ; i <= m ; ++ i) add(ed[i].a,ed[i].b);
     dfs_init(,);
     for (int i =  ; i <= cnt ; ++ i) {
         if (ocy(ext[i])) {
             rt = ext[i].first, ano = con[ext[i].second].b;
             modify(rt,ano);
             mar[tag(ext[i].second)] ++;
             break;
         }
     }
     memset (vis,,sizeof vis);
     if (rt) {
         int uns = dfs(rt,)>>;
         for (int i =  ; i <= m ; ++ i) ans[i] += mar[i] * uns;
         print();
     } else {
         if (dfs(,) != ) puts("NO");
         else print();
     }
     return ;
 }

小结：关于我卡在奇环无从下手，应该是缺乏与实际算法的运行相结合。