zyb的面试(广工14届比赛)

这道题目在上半年ZOJ模拟上年青岛赛区ACM题的时候就已经出现了。当时我不会写，本来想着赛后补题的最后因为懒惰又没补。

现在这道题又出现了。这是上天对我的惩罚啊！！！

所以这次铁了心也要补这题。然后我就找广工某大佬要了份题解，看得是一脸懵逼啊！

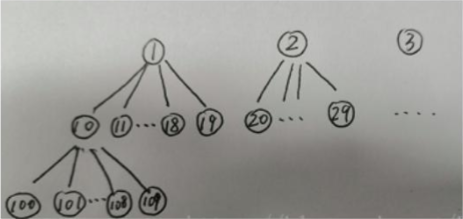
这个图就是算法的核心思想：将其分成9个多叉树，每颗树里面也能继续分。所以如果给出n，k。可以根据n计算每个树的大小，然后通过k跟这些树的大小比较，最后找到目标树，再在这颗树里面找到我们需要的答案。

PS：由于刚刚同学反映我写的看不懂，所以又重新写了一遍（希望没错，且你们能看得懂把！！！）

#include <bits/stdc++.h>
using namespace std;
#define re register
#define ll long long
void read(int &a)
{
    a=;
    int d=;
    char ch;
    while(ch=getchar(),ch>''||ch<'')
        if(ch=='-')
            d=-;
    a=ch-'';
    while(ch=getchar(),ch>=''&&ch<='')
        a=a*+ch-'';
    a*=d;
}
void write(int x)
{
    if(x<)
        putchar(),x=-x;
    if(x>)
        write(x/);
    putchar(x%+'');
}
const int L=;
int f[L],a[L],ten[L],cnt;///f存满十叉树的一共节点数，ten存当前层数的节点数
void geta(int n)
{
    cnt=;
    while(n)
    {
        a[cnt++]=n%;
        n/=;
    }
}
int main()
{
    f[]=ten[]=;
    for(re int i=;i<L;i++)
    {
        f[i]=f[i-]*+;
        ten[i]=ten[i-]*;
    }
    int T;
    read(T);
    while(T--)
    {
        int n,k;
        read(n);
        read(k);
        geta(n);
        int ans=,cmp=;
        for(re int i=cnt-;i>=&&k;i--)///枚举层数
            for(re int d=(ans==);d<;d++)///ans==0作用：因为第一位数不可能为0，所以第一个循环从1开始，之后的位数从0开始。
            {
                int siz=;
                if(==cmp)
                {
                    if(d<a[i])///若当前位置比a[i]小，说明d这颗树是有i层的满多叉树
                        siz=f[i];
                    else if(d==a[i])///相等则可能在中间某一段就停止的，就像样例中n==15，在1节点的完全多叉树中，但到15就结束了。
                        siz=f[i-]+n-(ans*+d)*ten[i]+;///计算这颗树有多少个点（这个公式分两部分看，f[i-1]就是确定的个数，之后不确定的个数通过总数n去减其他树的和就得到了）
                    else///若当前位置比a[i]大，那么在这之前肯定已经做过d==a[i]的，说明在那个之后后面的树只能是f[i-1]（因为第一棵树的第三层已经排了，说明其他树第二层排满）
                        siz=f[i-];
                }
                else if(cmp==-)
                    siz=f[i];
                else
                    siz=f[i-];
                if(k>siz)///如果k比这颗树的节点大，很明显他就在下一颗树上。
                    k-=siz;
                else///在这一颗树上向上找
                {
                    k--;///向上找只需要减一就行了
                    ans=ans*+d;///很明显，在这颗树上的话，这颗树的第一个点肯定是d
                    if(==cmp)
                        cmp=(d>a[i])-(d<a[i]);///若出现d>a[i]，则第一个肯定不是满二叉树，但他导致算树节点总数多了一层，所以要减一层。
                    break;
                }
            }
        printf("%d\n",ans);
    }
    return ;
}