hdu.5212.Code(莫比乌斯反演 && 埃氏筛）

Code

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 300    Accepted Submission(s): 124

Problem Description

WLD likes playing with codes.One day he is writing a function.Howerver,his computer breaks down because the function is too powerful.He is very sad.Can you help him?
The function:
int calc {      int res=0;      for(int i=1;i<=n;i++)          for(int j=1;j<=n;j++)          {              res+=gcd(a[i],a[j])*(gcd(a[i],a[j])-1);              res%=10007;          }      return res;
}

 

Input

There are Multiple Cases.(At MOST 10)
For each case:
The first line contains an integer N(1≤N≤10000).
The next line contains N integers a1,a2,...,aN(1≤ai≤10000).

 

Output

For each case:
Print an integer,denoting what the function returns.

 

Sample Input

5

1 3 4 2 4

 

Sample Output

64

Hint

gcd(x,y) means the greatest common divisor of x and y.

 #include<stdio.h>
 #include<string.h>
 #include<math.h>
 int F[ + ] , f[ + ];
 int num[ + ] ;
 int prime[ + ] ;
 int a[ + ] ;
 int mui[ + ] ;
 bool vis[ + ] ;
 int b[ + ] ;
 int n ;
 typedef long long ll ;
 void work_miu ()
 {
     memset (prime ,  , sizeof(prime)) ;
     memset (mui ,  , sizeof(mui)) ;
     memset (vis ,  , sizeof(vis)) ;
     for (int i =  ; i <=  ; i ++) a[i] = i ;
     for (int i =  ; i <=  ; i ++) {
         for (int j = i ; j <=  ; j += i ) {
             if (a[j] % i ==  && ! vis[j] ) {
                 int cnt =  ;
                 while (a[j] % i == ) {
                     a[j] /= i ;
                     cnt ++ ;
                 }
                 if (cnt > ) { vis[j] =  ; mui[j] =  ;}
                 else mui[j] ++ ;
             }
         }
     }
   /*  printf ("μ_source:\n") ;
     for (int i = 2 ; i <= 5 ; i ++) printf ("ID %d: %d\n" , i , mui[i]) ; puts (""); */
     mui[] =  ;
     for (int i =  ; i <=  ; i++) {
         if ( mui[i] ) mui[i] = (int) pow (- , mui[i]) ;
     }
 }

 void init() {
     mui[] = ;
     for (int i = ; i <= ; ++ i) {
         int x = i;
         int cnt = ;
         bool fuck = false;
         for (int j = ; j * j <= i; ++ j) {
             if (x % j == ) {
                 x /= j;
                 cnt ++;
                 if (x % j == ) {
                     fuck = true;
                     break;
                 }
             }
         }
         if (x != ) cnt ++;
         mui[i] = (cnt & ) ? - : ;
         if (fuck) mui[i] = ;
     }
 }

 int main ()
 {
    // freopen ("a.txt" , "r" , stdin ) ;
     work_miu () ;
     //init();
     while (~ scanf ("%d", &n)  )  {
         int x ;
         memset (F ,  , sizeof(F)) ;
         memset (num ,  , sizeof(num) ) ;
         memset (f ,  , sizeof(f)) ;
         for (int i =  ; i < n ; i ++) {
                 scanf ("%d" , &b[i]) ;
                 num[ b[i] ] ++ ;
         }
         ll sum =  ;
         for (int i =  ; i >=  ; i --) {
             int cnt =  ;
             for (int j = i ; j <=  ; j += i) {
                 cnt += num[j] ;
             }
             if (cnt > ) {
                 F[i] = (cnt * cnt - cnt) /  ;
                 for (int j = i ; j <=  ; j += i ) {
                     f[i] += mui[j / i] * F[j] ;
                 }
            /*     if (f[i] != 0) {
                     printf ("ID %d : %d\n" , i , f[i]) ;
                 }*/
                 sum += 1ll * f[i] * (i * i - i ) ;
             }
         } //puts ("") ;
       /*  puts ("F(X) :") ;
         for (int i = 1 ; i <= 5 ; i ++) printf ("ID %d: %d \n" , i , F[i]) ; puts ("") ;
         printf ("μ：\n") ;
         for (int i = 1 ; i <= 5 ; i ++) printf ("ID %d: %d\n" , i , mui[i]) ; puts ("") ;
         printf ("sum=%d\n" , sum ) ; */
         sum *=  ;
         for (int i =  ; i < n ; i ++) {
             sum += b[i] * b[i] - b[i] ;
         }
         printf ("%I64d\n" , sum % ) ;
     }
     return  ;
 }

复杂度这里，因为用的是埃帅，所以为O（nlog(log(n)) ) .

我从杰哥那里学到了一种和百度上不同的莫比乌斯反演写法(个人感觉不错）：

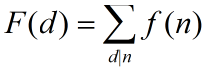
n为d的所有倍数。

则：aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWcAAAA3CAIAAABfIxyZAAAK00lEQVR4nO2czWsbSRrG51+oW4EYhKB3QAhjhA3CiGCBiFiiIYgQaCyICLjJQRh7sCAGL+gwzoKGaQaFZQxig33RjnFGhyZR2GgRZAMjhp14V4yCSQa0YMWEhkAzsOjQt9pD66vVLan6U1/v7zRhWu56+n3r6aq3qvozAgAAYITPpt0AAADmDHANAACMAa4BAIAxwDUAADAGuAYAAMYA1wAAwBjgGgAAGANcAwAAY4BrAIDtyPX8rTU/g/13C69eHMTWYuydde/qVqEuT7tltgCuAQB20zyOxR6/v8iFEEI4krtoEyKXUgghTph202wBXAMAbObj3+5Hc7VmIY4Qij1+LxNCiFRkEUKp0kIMNsA1AMAJFJsI8w1CCCGywGGEwrnFmKIsqmu8y0dQB+z1r4yH8aAhfHuVhQjvkjCL0a5mfAgFDl/L/X8Fs7XFyKpFdQ0ildNMNylSJXHi9bJ0ffnTU35704sRQgixRcmFVgL2MHvRrmUDCOFUqU0I6ZtGu7y/tv/8fzbfy3UW1jUIket8BBvIpO7PPrziEwxCkcfvnWwdYC8zFu2WUtQ4bhJCCGnwYYQCh68/FFnGQONmFsdcQ/5Q2r3x4OnH8Vf9+pf4bf6i7VQb+pnUCyAdosAxgWzN3F2plBPitHo3aV/wtyPf/Gv8Rb8/++rGbumDU4P06USb6Iuv7nsRw/XENk7u+n3BjdDto1dq/SZTYMo55pBriALHMHsvJJ0MaT5h/V6MOnM+uc5HsINFIrHIdjPJ2F3Es+3Qw5djx5Ji5WCTWQ8GmMTAOvwY5VqcVm8/eprlOh/xxB+/1UtNdbRFgWOMjAQMt87BaI9gnHja3xtNgannmCOuIZXTjC/9YuSDlIrswJyveRxDoVzdiYYQojziTib1alN2IFf2fCgQDvsGKuUTlWtxWL296Gpu5CO4u76ohyracmXP93mq5FjNyKloj2KSeBoMpsAM5JgTrtHgw2PLxcoqVH8QKZ0lsZPVR7maMVQqo6Oa8SF07/jZtzsPT7sjwEnK9XBavZ3oaJYEzofZ4uinOhztN0dBZGE6MBFnoq3PRPGUf8ZICsxCjjngGm+OguPHh9WMD6HQo4veFbLAYZQ4dS7CJktl43iXj6hFEArl+o1zWj0hhJDLp4ffVizeQ0ezdJbEvVGjLppoN/gw+uLwtbWmjMOBaOszWTwlBlJgJnLMkmuIr4+3oytR9s66P7HzcOfhDw2ipJZ2Abx9eb4bXYmydzZWNzeY4SXyViHu8G7bwVJZb2xtBYFDCN07H8wYjXLK0wjOqyeEkGYhbrV+r6O5nMY6pcfx0a5mfPbEYCT2RbtZiGMUyb9T/iWV90OhBz+2Ov9TX7wZ9FKArndNJcfMu4ZU3vVjzP71v21CxNNEb7OMwGkiJVUP1jFWSkbKpUO5R8pp7PjsXiylfKZKZUP857s/rqz4vbi7oyia6wwXh5VTn0ZwQz1R5vzhR6bq6aM0N/gwwpygepgTo/0uH3F+b7U90W4V4qgvUF2P0xVvluEUoO1d08kxs66hzB678ytl7po4FfVSQrm0W5sanuYqNPjwCCtsPf/zzgS+q1JO2OwrlSmRGd8Z6E8jjFY/xC9PJj2LibAbqwn+lZnlTz3N2lykibbOi6XDjEV7IK8J6Uy2+mLs7IjqFKDuXQ7kGA0mXUM6S+KBYNSygW4eNPiwusnKpb1RVS0b0Imi5lcOIdeywW6pjBPMV4cGBPfQ1UB1GsEt9Qrty/PMpn+D/bpYN/QA9DQLHFJ3HKpoa37lEJajXc34BsJVz4VUYvRlbG5u/mES2jupUsBA7yJkGjlm0jWqGd/Ae+ddPtITqWmdzqXasod7/aYz5cWR3M906916tApxrQpdDVSnEdx0jfbl+W40tHX07N/XxvTratZ0HKpou+UaVqPd4MMDzVfPVoi9MlQpYKB39S53NcdMukY5jftPTL0gX0ohVbVWdakyyk2cfijvrzx82f97tWxgxDDSzjErIZ08Gti1Z4pyGiNNSVqjnNCeRhitfgiLM5QHtwLIc3N4e6IVzfVcSL0eQhNtqchq/5LCTEVb2RXe7bwDYtYOq4ToiLeAKgUM9C5ie47RYGWGojyxzvRRNflbe3Qx5tJQ7qKyxwwuc8ullNFdwKaQfysmmU7RyAL1XEiz6kq0ymlPI7ikXhQ4v3np+ppbhbi61EET7Xou5MqhYovRVob6ncC0L3IRjFDo0c8vemI04i00VZUCBnrXdHLM9BqKWDnY9PqjidiNjeDng/Mo6SypXhqWfytur3qCt9loaIs/5bdWPYx/7ZZqb3wtG3DhGLEocAxez7ywehJCKrK6p6s1yilPI7iiXhI4hj01LX2U5jdHQfX7dnK0pSKLbNgaNQnL0Vbe4V6G2bjDxm7c64hhVm/2xGjEm2Y4Beh711RyzPour1Yhri54SWdJbGwGZWa7m1FsmZm0P11dXUuVjA/pbuk1rpwQd9QT0v50ZbCQ0f/hOM1vjoLGJveywGHHTcOGaI+oyaigF68+jzPM6BSwoXeNv4EpzLhG4/ubHoSSP/xOCBH/8VUQDY0C5WqGMbARTa5lgzh+bG0v/wREgbM+M2mdJDBCOBwOoeDha70/ZVA5Ie6ot8Bkzc1CHBuYMItFFjN7FUcP+toRbWVhYtL8w4j4od0efdQpYHPv0t7ABsy4hlg5iPrXb23v3P8ytBL68uD81+GXmChwDO3MtVmIeyxXGsYiChyD/WljL57mcWz43SrX8zc9XwTW17aORzbXiHJC3FBvDQrNcp2PYMops1zNMFYHfBOwKdpDezNGQS9ef+sK0aSAvb1L5wY24NT3NeQ6H6HYwCzX+Yjf0SwyNVaV63wEmxzRUSrvXuqsepcQBY6h2IFprR5Lg33RFi+e/1i9pGkqpXjNeZzevY2nwLRzzMFvecnS9dWnCY/d9GybEhNj1fbleXodW/rII41yQpxX7yYUWmgfi2mmE20yWvz48zjjfjmRqebYAn8BkIhC2k/14pGl66ury5+eH3/Ndj8kiax+NAFwmZmL9uTTV3PLwrrG4LFHE4BpzBWzF22a8zhzy6K6xse/f2NlF6XlT1EAbjJ70aY6jzO3LKprAMA0oTqPM7eAawCA/VCdvppbwDUAwH5ozuPML8vlGr88ubfpQzh5JpEGH+592A1YSAaiLXA4XXb15hSnr+aX5XINpZYd5hsEXGMJ6EfbfddYaJbMNWrZAGIO/knANZaBfrTBNWxlOVxDrBzE1u5sJzc8HmXE2nMNuZ6/veZnvJtfsvH7O8l1763vnfx4NuACOtHuuAZE2x6WwTUa+Qj2pEoSEU8TCEfyDUK6riELnDd9dBhAnsRJU/mmG4xA5hvdaCuuAdG2iSVwjWrGhzzpsqz8lzJi7bmGdH399jjeeSU1+HD35QTMKfrR7rgGRNseFt81GnwY4cRJS9lrg7nz62tJHqhryKVU5wPPrUIc4UTh7bWjR6wAJxkR7V5dA6JtB4vvGq1CHOF0WTlBhG/+6SARyQ+uodSyAeTZfdn5Ml0in0960+VF2cS3dIyIds81INp2sPiuQURhd9XPZvZjseiGh/Gv3T1pkr5rfDxJIE+qJBEiVw/8mFmNbp1AhWx+0Y921zUg2rawBK6hD6y8LhOw8mor4BrAEgCuYSvgGsASAK5hK0vrGgAAmARcAwAAY4BrAABgjP8DcZJ3UH+Jf3oAAAAASUVORK5CYII=" alt="" />

μ(1) = 1 ;

k = p1 * p2 * p3 ……*pr（k由r个不同的质数组成）则μ(k) = -1^k ;

其他情况，μ (k) = 0 ;

这道题F(x)指的是x的倍数的对数的个数有多少。

f(x) = 最大公约数为x的多数有多少。

比如：

F(1) = f(1) + f(2) + f(3) + f(4) = 7 + 2 + 0 + 1 = 10

得到F(x)是非常容易的可以统计x的倍数有多少个，比如说=cnt ；

那么此时的F(x) = (cnt * cnt - cnt) / 2 ;(稍微想想就能想通）

Then ， it's the time for 。。。。。