P3355 骑士共存问题 网络流

骑士共存

题目描述

在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

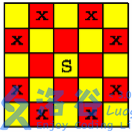
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入输出格式

输入格式：

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

输出格式：

将计算出的共存骑士数输出

输入输出样例

输入样例#1： 复制

3 2
1 1
3 3

输出样例#1： 复制

5

这个题目和刚刚那个题目很像也是一个网络流的最大独立集题目，
既然如此，我们就照着那个题目来分析。
首先我们要把可以两个互斥的格子进行分开，然后和之前的一比对，会发现如果两个任何两个互斥的骑士他们的横纵坐标之和的奇偶性不相同。
所以这就说明，我们可以像之前一样，用这个奇偶性把他们分成两个部分，还是一样，在同一个部分的肯定不互斥，不在同一个部分可能互斥。
这个多了一个障碍物，我觉得这个可以理解为这个格子不见了，所以不要管他就可以了。
这个建图就是 s连接一个部分，容量就是1，一个部分与另一个部分互斥的数相连，容量为inf，另一个部分和t相连。
那么这个我们再理解一下，所以这个最大流就意味着，最少的不能占的地方。
所以 ans=没有障碍物的总格子数量 - 最大流，

#include <cstdio>
#include <cstdlib>
#include <queue>
#include <vector>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#define inf 0x3f3f3f3f
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 1e5 + ;
struct edge
{
    int u, v, c, f;
    edge(int u, int v, int c, int f) :u(u), v(v), c(c), f(f) {}
};
vector<edge>e;
vector<int>G[maxn];
int level[maxn];//BFS分层，表示每个点的层数
int iter[maxn];//当前弧优化
int m;
void init(int n)
{
    for (int i = ; i <= n; i++)G[i].clear();
    e.clear();
}
void add(int u, int v, int c)
{
    e.push_back(edge(u, v, c, ));
    e.push_back(edge(v, u, , ));
    m = e.size();
    G[u].push_back(m - );
    G[v].push_back(m - );
    //printf("ww %d %d %d\n", u, v, c);
}
void BFS(int s)//预处理出level数组
//直接BFS到每个点
{
    memset(level, -, sizeof(level));
    queue<int>q;
    level[s] = ;
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        for (int v = ; v < G[u].size(); v++)
        {
            edge& now = e[G[u][v]];
            if (now.c > now.f && level[now.v] < )
            {
                level[now.v] = level[u] + ;
                q.push(now.v);
            }
        }
    }
}
int dfs(int u, int t, int f)//DFS寻找增广路
{
    if (u == t)return f;//已经到达源点，返回流量f
    for (int &v = iter[u]; v < G[u].size(); v++)
        //这里用iter数组表示每个点目前的弧，这是为了防止在一次寻找增广路的时候，对一些边多次遍历
        //在每次找增广路的时候，数组要清空
    {
        edge &now = e[G[u][v]];
        if (now.c - now.f >  && level[u] < level[now.v])
            //now.c - now.f > 0表示这条路还未满
            //level[u] < level[now.v]表示这条路是最短路，一定到达下一层，这就是Dinic算法的思想
        {
            int d = dfs(now.v, t, min(f, now.c - now.f));
            if (d > )
            {
                now.f += d;//正向边流量加d
                e[G[u][v] ^ ].f -= d;
                //反向边减d，此处在存储边的时候两条反向边可以通过^操作直接找到
                return d;
            }
        }
    }
    return ;
}
int Maxflow(int s, int t)
{
    int flow = ;
    for (;;)
    {
        BFS(s);
        if (level[t] < )return flow;//残余网络中到达不了t，增广路不存在
        memset(iter, , sizeof(iter));//清空当前弧数组
        int f;//记录增广路的可增加的流量
        while ((f = dfs(s, t, INF)) > )
        {
            flow += f;
        }
    }
    return flow;
}
bool vis[][];
int dx[] = { -,-,-,-,,,, };
int dy[] = { -,-,,,,,-,- };

int main()
{
    int n, m;
    cin >> n >> m;
    memset(vis, , sizeof(vis));
    for(int i=;i<=m;i++)
    {
        int x, y;
        cin >> x >> y;
        vis[x][y] = ;
    }
    int s = , t = n * n + ;
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            if (vis[i][j]) continue;
            int ex = (i - )*n + j;
            if((i+j)&)
            {
                add(s, ex, );
                for(int k=;k<;k++)
                {
                    int tx = i + dx[k];
                    int ty = j + dy[k];

                    if (tx > n || tx< || ty>n || ty < ) continue;
                    if (vis[tx][ty]) continue;

                    //printf("i=%d j=%d tx=%d ty=%d\n", i, j, tx, ty);
                    int ed = (tx - )*n + ty;
                    add(ex, ed, inf);
                }
            }
            else add(ex, t, );
        }
    }
    int ans = Maxflow(s, t);
    //printf("%d\n", ans);
    printf("%d\n", n*n - m - ans);
    return ;
}