数据结构和算法(Golang实现)(15)常见数据结构-列表
列表
一、列表 List
我们又经常听到列表 List数据结构，其实这只是更宏观的统称，表示存放数据的队列。
列表
List：存放数据，数据按顺序排列，可以依次入队和出队，有序号关系，可以取出某序号的数据。先进先出的队列 (queue)和先进后出的栈（stack）都是列表。大家也经常听说一种叫线性表的数据结构，表示具有相同特性的数据元素的有限序列，实际上就是列表的同义词。
我们一般写算法进行数据计算，数据处理，都需要有个地方来存数据，我们可以使用封装好的数据结构List：
列表的实现有顺序表示或链式表示。
顺序表示：指的是用一组地址连续的存储单元依次存储线性表的数据元素，称为线性表的顺序存储结构。它以物理位置相邻来表示线性表中数据元素间的逻辑关系，可随机存取表中任一元素。顺序表示的又叫顺序表，也就是用数组来实现的列表。
链式表示：指的是用一组任意的存储单元存储线性表中的数据元素，称为线性表的链式存储结构。它的存储单元可以是连续的，也可以是不连续的。在表示数据元素之间的逻辑关系时，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息，也就是用链表来实现的列表。
我们在前面已经实现过这两种表示的数据结构：先进先出的队列 (queue)和先进后出的栈（stack）。接下来我们会来实现链表形式的双端列表，也叫双端队列，这个数据结构应用场景更广泛一点。在实际工程应用上，缓存数据库Redis的列表List基本类型就是用它来实现的。
二、实现双端列表
双端列表，也可以叫双端队列
我们会用双向链表来实现这个数据结构：
// 双端列表，双端队列
type DoubleList struct {
head *ListNode // 指向链表头部
tail *ListNode // 指向链表尾部
len int // 列表长度
lock sync.Mutex // 为了进行并发安全pop操作
}
// 列表节点
type ListNode struct {
pre *ListNode // 前驱节点
next *ListNode // 后驱节点
value string // 值
}
设计结构体DoubleList指向队列头部head和尾部tail的指针字段，方便找到链表最前和最后的节点，并且链表节点之间是双向链接的，链表的第一个元素的前驱节点为nil，最后一个元素的后驱节点也为nil。如图：
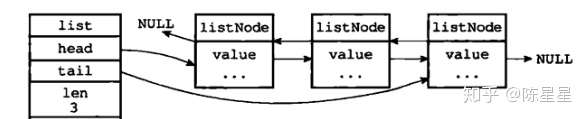
我们实现的双端列表和Golang标准库container/list中实现的不一样，感兴趣的可以阅读标准库的实现。
2.1.列表节点普通操作
// 获取节点值
func (node *ListNode) GetValue() string {
return node.value
}
// 获取节点前驱节点
func (node *ListNode) GetPre() *ListNode {
return node.pre
}
// 获取节点后驱节点
func (node *ListNode) GetNext() *ListNode {
return node.next
}
// 是否存在后驱节点
func (node *ListNode) HashNext() bool {
return node.pre != nil
}
// 是否存在前驱节点
func (node *ListNode) HashPre() bool {
return node.next != nil
}
// 是否为空节点
func (node *ListNode) IsNil() bool {
return node == nil
}
以上是对节点结构体ListNode的操作，主要判断节点是否为空，有没有后驱和前驱节点，返回值等，时间复杂度都是O(1)。
2.2.从头部开始某个位置前插入新节点
// 添加节点到链表头部的第N个元素之前，N=0表示新节点成为新的头部
func (list *DoubleList) AddNodeFromHead(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度，一定找不到，panic
if n > list.len {
panic("index out")
}
// 先找出头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
// 新节点
newNode := new(ListNode)
newNode.value = v
// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
if node.IsNil() {
list.head = newNode
list.tail = newNode
} else {
// 定位到的节点，它的前驱
pre := node.pre
// 如果定位到的节点前驱为nil，那么定位到的节点为链表头部，需要换头部
if pre.IsNil() {
// 将新节点链接在老头部之前
newNode.next = node
node.pre = newNode
// 新节点成为头部
list.head = newNode
} else {
// 将新节点插入到定位到的节点之前
// 定位到的节点的前驱节点 pre 现在链接到新节点上
pre.next = newNode
newNode.pre = pre
// 定位到的节点的后驱节点 node.next 现在链接到新节点上
node.next.pre = newNode
newNode.next = node.next
}
}
// 列表长度+1
list.len = list.len + 1
}
首先加锁实现并发安全。然后判断索引是否超出列表长度：
// 索引超过列表长度，一定找不到，panic
if n > list.len {
panic("index out")
}
如果n=0表示新节点想成为新的链表头部，n=1表示插入到链表头部数起第二个节点之前，新节点成为第二个节点，以此类推。
首先，找出头部：node := list.head，然后往后面遍历，定位到索引指定的节点node：
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
接着初始化新节点：newNode := new(ListNode)。
定位到的节点有三种情况，我们需要在该节点之前插入新节点：
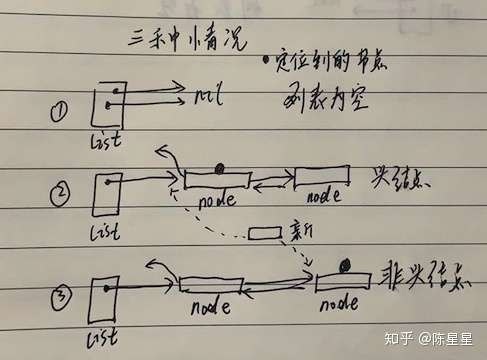
判断定位到的节点node是否为空，如果为空，表明列表没有元素，将新节点设置为新头部和新尾部。
否则找到定位到的节点的前驱节点：pre := node.pre。
如果前驱节点为空：pre.IsNil()，表明定位到的节点node为头部，那么新节点要取代它，成为新的头部：
if pre.IsNil() {
// 将新节点链接在老头部之前
newNode.next = node
node.pre = newNode
// 新节点成为头部
list.head = newNode
}
新节点成为新的头部，需要将新节点的后驱设置为老头部：newNode.next = node，老头部的前驱为新头部：node.pre = newNode，并且新头部变化：list.head = newNode。
如果定位到的节点的前驱节点不为空，表明定位到的节点node不是头部节点，那么我们只需将新节点链接到节点node之前即可：
// 定位到的节点的前驱节点 pre 现在链接到新节点前
pre.next = newNode
newNode.pre = pre
// 定位到的节点链接到新节点之后
newNode.next = node
node.pre = newNode
先将定位到的节点的前驱节点和新节点绑定，因为现在新节点插在前面了，把定位节点的前驱节点的后驱设置为新节点：pre.next = newNode，新节点的前驱设置为定位节点的前驱节点：newNode.pre = pre。
同时，定位到的节点现在要链接到新节点之后，所以新节点的后驱设置为：newNode.next = node，定位到的节点的前驱设置为：node.pre = newNode。
最后，链表长度加一。
大部分时间花在遍历位置上，如果n=0，那么时间复杂度为O(1)，否则为O(n)。
2.3.从尾部开始某个位置后插入新节点
// 添加节点到链表尾部的第N个元素之后，N=0表示新节点成为新的尾部
func (list *DoubleList) AddNodeFromTail(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度，一定找不到，panic
if n > list.len {
panic("index out")
}
// 先找出尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.pre
}
// 新节点
newNode := new(ListNode)
newNode.value = v
// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
if node.IsNil() {
list.head = newNode
list.tail = newNode
} else {
// 定位到的节点，它的后驱
next := node.next
// 如果定位到的节点后驱为nil，那么定位到的节点为链表尾部，需要换尾部
if next.IsNil() {
// 将新节点链接在老尾部之后
node.next = newNode
newNode.pre = node
// 新节点成为尾部
list.tail = newNode
} else {
// 将新节点插入到定位到的节点之后
// 新节点链接到定位到的节点之后
newNode.pre = node
node.next = newNode
// 定位到的节点的后驱节点链接在新节点之后
newNode.next = next
next.pre = newNode
}
}
// 列表长度+1
list.len = list.len + 1
}
操作和头部插入节点相似，自行分析。
2.4.从头部开始某个位置获取列表节点
// 从头部开始往后找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromHead(n int) *ListNode {
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取头部节点
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
return node
}
如果索引超出或等于列表长度，那么找不到节点，返回空。
否则从头部开始遍历，拿到节点。
时间复杂度为：O(n)。
2.5.从尾部开始某个位置获取列表节点
// 从尾部开始往前找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromTail(n int) *ListNode {
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取尾部节点
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.pre
}
return node
}
操作和从头部获取节点一样，请自行分析。
2.6.从头部开始移除并返回某个位置的节点
// 从头部开始往后找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromHead(n int) *ListNode {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
// 移除的节点的前驱和后驱
pre := node.pre
next := node.next
// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
if pre.IsNil() && next.IsNil() {
list.head = nil
list.tail = nil
} else if pre.IsNil() {
// 表示移除的是头部节点，那么下一个节点成为头节点
list.head = next
next.pre = nil
} else if next.IsNil() {
// 表示移除的是尾部节点，那么上一个节点成为尾节点
list.tail = pre
pre.next = nil
} else {
// 移除的是中间节点
pre.next = next
next.pre = pre
}
// 节点减一
list.len = list.len - 1
return node
}
首先加并发锁实现并发安全。先判断索引是否超出列表长度：n >= list.len，如果超出直接返回空指针。
获取头部，然后遍历定位到第N+1个位置的元素：node = node.next。
定位到的并要移除的节点有三种情况发生：
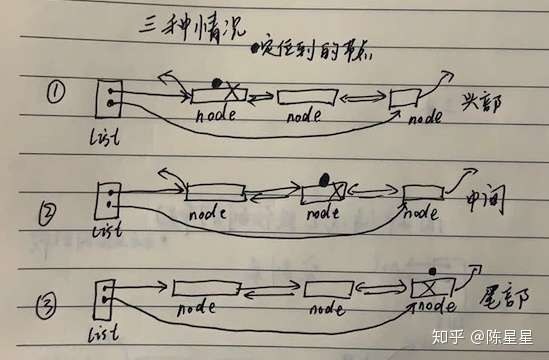
查看要移除的节点的前驱和后驱：
// 移除的节点的前驱和后驱
pre := node.pre
next := node.next
如果前驱和后驱都为空：pre.IsNil() && next.IsNil()，那么要移除的节点是链表中唯一的节点，直接将列表头部和尾部置空即可。
如果前驱节点为空：pre.IsNil()，表示移除的是头部节点，那么头部节点的下一个节点要成为新的头部：list.head = next，并且这时新的头部前驱要设置为空：next.pre = nil。
同理，如果后驱节点为空：next.IsNil()，表示移除的是尾部节点，需要将尾部节点的前一个节点设置为新的尾部：list.tail = pre，并且这时新的尾部后驱要设置为空：pre.next = nil。
如果移除的节点处于两个节点之间，那么将这两个节点链接起来即可:
// 移除的是中间节点
pre.next = next
next.pre = pre
最后，列表长度减一。
主要的耗时用在定位节点上，其他的操作都是链表链接，可以知道时间复杂度为：O(n)。
2.7.从尾部开始移除并返回某个位置的节点
// 从尾部开始往前找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromTail(n int) *ListNode {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.pre
}
// 移除的节点的前驱和后驱
pre := node.pre
next := node.next
// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
if pre.IsNil() && next.IsNil() {
list.head = nil
list.tail = nil
} else if pre.IsNil() {
// 表示移除的是头部节点，那么下一个节点成为头节点
list.head = next
next.pre = nil
} else if next.IsNil() {
// 表示移除的是尾部节点，那么上一个节点成为尾节点
list.tail = pre
pre.next = nil
} else {
// 移除的是中间节点
pre.next = next
next.pre = pre
}
// 节点减一
list.len = list.len - 1
return node
}
操作和从头部移除节点相似，请自行分析。
2.8.完整例子
package main
import (
"fmt"
"sync"
)
// 双端列表，双端队列
type DoubleList struct {
head *ListNode // 指向链表头部
tail *ListNode // 指向链表尾部
len int // 列表长度
lock sync.Mutex // 为了进行并发安全pop操作
}
// 列表节点
type ListNode struct {
pre *ListNode // 前驱节点
next *ListNode // 后驱节点
value string // 值
}
// 获取节点值
func (node *ListNode) GetValue() string {
return node.value
}
// 获取节点前驱节点
func (node *ListNode) GetPre() *ListNode {
return node.pre
}
// 获取节点后驱节点
func (node *ListNode) GetNext() *ListNode {
return node.next
}
// 是否存在后驱节点
func (node *ListNode) HashNext() bool {
return node.pre != nil
}
// 是否存在前驱节点
func (node *ListNode) HashPre() bool {
return node.next != nil
}
// 是否为空节点
func (node *ListNode) IsNil() bool {
return node == nil
}
// 返回列表长度
func (list *DoubleList) Len() int {
return list.len
}
// 添加节点到链表头部的第N个元素之前，N=0表示新节点成为新的头部
func (list *DoubleList) AddNodeFromHead(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度，一定找不到，panic
if n > list.len {
panic("index out")
}
// 先找出头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
// 新节点
newNode := new(ListNode)
newNode.value = v
// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
if node.IsNil() {
list.head = newNode
list.tail = newNode
} else {
// 定位到的节点，它的前驱
pre := node.pre
// 如果定位到的节点前驱为nil，那么定位到的节点为链表头部，需要换头部
if pre.IsNil() {
// 将新节点链接在老头部之前
newNode.next = node
node.pre = newNode
// 新节点成为头部
list.head = newNode
} else {
// 将新节点插入到定位到的节点之前
// 定位到的节点的前驱节点 pre 现在链接到新节点前
pre.next = newNode
newNode.pre = pre
// 定位到的节点链接到新节点之后
newNode.next = node
node.pre = newNode
}
}
// 列表长度+1
list.len = list.len + 1
}
// 添加节点到链表尾部的第N个元素之后，N=0表示新节点成为新的尾部
func (list *DoubleList) AddNodeFromTail(n int, v string) {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过列表长度，一定找不到，panic
if n > list.len {
panic("index out")
}
// 先找出尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.pre
}
// 新节点
newNode := new(ListNode)
newNode.value = v
// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
if node.IsNil() {
list.head = newNode
list.tail = newNode
} else {
// 定位到的节点，它的后驱
next := node.next
// 如果定位到的节点后驱为nil，那么定位到的节点为链表尾部，需要换尾部
if next.IsNil() {
// 将新节点链接在老尾部之后
node.next = newNode
newNode.pre = node
// 新节点成为尾部
list.tail = newNode
} else {
// 将新节点插入到定位到的节点之后
// 新节点链接到定位到的节点之后
newNode.pre = node
node.next = newNode
// 定位到的节点的后驱节点链接在新节点之后
newNode.next = next
next.pre = newNode
}
}
// 列表长度+1
list.len = list.len + 1
}
// 返回列表链表头结点
func (list *DoubleList) First() *ListNode {
return list.head
}
// 返回列表链表尾结点
func (list *DoubleList) Last() *ListNode {
return list.tail
}
// 从头部开始往后找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromHead(n int) *ListNode {
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取头部节点
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
return node
}
// 从尾部开始往前找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromTail(n int) *ListNode {
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取尾部节点
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.pre
}
return node
}
// 从头部开始往后找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromHead(n int) *ListNode {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取头部
node := list.head
// 往后遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.next
}
// 移除的节点的前驱和后驱
pre := node.pre
next := node.next
// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
if pre.IsNil() && next.IsNil() {
list.head = nil
list.tail = nil
} else if pre.IsNil() {
// 表示移除的是头部节点，那么下一个节点成为头节点
list.head = next
next.pre = nil
} else if next.IsNil() {
// 表示移除的是尾部节点，那么上一个节点成为尾节点
list.tail = pre
pre.next = nil
} else {
// 移除的是中间节点
pre.next = next
next.pre = pre
}
// 节点减一
list.len = list.len - 1
return node
}
// 从尾部开始往前找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromTail(n int) *ListNode {
// 加并发锁
list.lock.Lock()
defer list.lock.Unlock()
// 索引超过或等于列表长度，一定找不到，返回空指针
if n >= list.len {
return nil
}
// 获取尾部
node := list.tail
// 往前遍历拿到第 N+1 个位置的元素
for i := 1; i <= n; i++ {
node = node.pre
}
// 移除的节点的前驱和后驱
pre := node.pre
next := node.next
// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
if pre.IsNil() && next.IsNil() {
list.head = nil
list.tail = nil
} else if pre.IsNil() {
// 表示移除的是头部节点，那么下一个节点成为头节点
list.head = next
next.pre = nil
} else if next.IsNil() {
// 表示移除的是尾部节点，那么上一个节点成为尾节点
list.tail = pre
pre.next = nil
} else {
// 移除的是中间节点
pre.next = next
next.pre = pre
}
// 节点减一
list.len = list.len - 1
return node
}
func main() {
list := new(DoubleList)
// 在列表头部插入新元素
list.AddNodeFromHead(0, "I")
list.AddNodeFromHead(0, "love")
list.AddNodeFromHead(0, "you")
// 在列表尾部插入新元素
list.AddNodeFromTail(0, "may")
list.AddNodeFromTail(0, "happy")
// 正常遍历，比较慢
for i := 0; i < list.Len(); i++ {
// 从头部开始索引
node := list.IndexFromHead(i)
// 节点为空不可能，因为list.Len()使得索引不会越界
if !node.IsNil() {
fmt.Println(node.GetValue())
}
}
fmt.Println("----------")
// 正常遍历，特别快
// 先取出第一个元素
first := list.First()
for !first.IsNil() {
// 如果非空就一直遍历
fmt.Println(first.GetValue())
// 接着下一个节点
first = first.GetNext()
}
fmt.Println("----------")
// 元素一个个 POP 出来
for {
node := list.PopFromHead(0)
if node.IsNil() {
// 没有元素了，直接返回
break
}
fmt.Println(node.GetValue())
}
fmt.Println("----------")
fmt.Println("len", list.Len())
}
输出：
you
love
I
may
happy
----------
you
love
I
may
happy
----------
you
love
I
may
happy
----------
len 0
首先，先从列表头部插入三个新元素，然后从尾部插入两个新元素，然后用三种方式进行遍历，两种只是查看元素，一种是遍历移除元素。
系列文章入口
我是陈星星，欢迎阅读我亲自写的 数据结构和算法(Golang实现)，文章首发于 阅读更友好的GitBook。
- 数据结构和算法(Golang实现)(1)简单入门Golang-前言
- 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
- 数据结构和算法(Golang实现)(3)简单入门Golang-流程控制语句
- 数据结构和算法(Golang实现)(4)简单入门Golang-结构体和方法
- 数据结构和算法(Golang实现)(5)简单入门Golang-接口
- 数据结构和算法(Golang实现)(6)简单入门Golang-并发、协程和信道
- 数据结构和算法(Golang实现)(7)简单入门Golang-标准库
- 数据结构和算法(Golang实现)(8.1)基础知识-前言
- 数据结构和算法(Golang实现)(8.2)基础知识-分治法和递归
- 数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号
- 数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法
- 数据结构和算法(Golang实现)(11)常见数据结构-前言
- 数据结构和算法(Golang实现)(12)常见数据结构-链表
- 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
- 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
- 数据结构和算法(Golang实现)(15)常见数据结构-列表
- 数据结构和算法(Golang实现)(16)常见数据结构-字典
- 数据结构和算法(Golang实现)(17)常见数据结构-树
- 数据结构和算法(Golang实现)(18)排序算法-前言
- 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
- 数据结构和算法(Golang实现)(20)排序算法-选择排序
- 数据结构和算法(Golang实现)(21)排序算法-插入排序
- 数据结构和算法(Golang实现)(22)排序算法-希尔排序
- 数据结构和算法(Golang实现)(23)排序算法-归并排序
- 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
- 数据结构和算法(Golang实现)(25)排序算法-快速排序
- 数据结构和算法(Golang实现)(26)查找算法-哈希表
- 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
- 数据结构和算法(Golang实现)(28)查找算法-AVL树
- 数据结构和算法(Golang实现)(29)查找算法-2-3树和左倾红黑树
- 数据结构和算法(Golang实现)(30)查找算法-2-3-4树和普通红黑树
数据结构和算法(Golang实现)(15)常见数据结构-列表的更多相关文章
- 数据结构和算法(Golang实现)(11)常见数据结构-前言
常见数据结构及算法 数据结构主要用来组织数据,也作为数据的容器,载体. 各种各样的算法,都需要使用一定的数据结构来组织数据. 常见的典型数据结构有: 链表 栈和队列 树 图 上述可以延伸出各种各样的术 ...
- 数据结构和算法(Golang实现)(12)常见数据结构-链表
链表 讲数据结构就离不开讲链表.因为数据结构是用来组织数据的,如何将一个数据关联到另外一个数据呢?链表可以将数据和数据之间关联起来,从一个数据指向另外一个数据. 一.链表 定义: 链表由一个个数据节点 ...
- 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
可变长数组 因为数组大小是固定的,当数据元素特别多时,固定的数组无法储存这么多的值,所以可变长数组出现了,这也是一种数据结构.在Golang语言中,可变长数组被内置在语言里面:切片slice. sli ...
- 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
栈和队列 一.栈 Stack 和队列 Queue 我们日常生活中,都需要将物品排列,或者安排事情的先后顺序.更通俗地讲,我们买东西时,人太多的情况下,我们要排队,排队也有先后顺序,有些人早了点来,排完 ...
- 数据结构和算法(Golang实现)(16)常见数据结构-字典
字典 我们翻阅书籍时,很多时候都要查找目录,然后定位到我们要的页数,比如我们查找某个英文单词时,会从英语字典里查看单词表目录,然后定位到词的那一页. 计算机中,也有这种需求. 一.字典 字典是存储键值 ...
- 数据结构和算法(Golang实现)(17)常见数据结构-树
树 树是一种比较高级的基础数据结构,由n个有限节点组成的具有层次关系的集合. 树的定义: 有节点间的层次关系,分为父节点和子节点. 有唯一一个根节点,该根节点没有父节点. 除了根节点,每个节点有且只有 ...
- 数据结构和算法(Golang实现)(25)排序算法-快速排序
快速排序 快速排序是一种分治策略的排序算法,是由英国计算机科学家Tony Hoare发明的, 该算法被发布在1961年的Communications of the ACM 国际计算机学会月刊. 注:A ...
- 数据结构和算法(Golang实现)(1)简单入门Golang-前言
数据结构和算法在计算机科学里,有非常重要的地位.此系列文章尝试使用 Golang 编程语言来实现各种数据结构和算法,并且适当进行算法分析. 我们会先简单学习一下Golang,然后进入计算机程序世界的第 ...
- 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
包.变量和函数 一.举个例子 现在我们来建立一个完整的程序main.go: // Golang程序入口的包名必须为 main package main // import "golang&q ...
随机推荐
- 2018 巅峰极客CTF misc writeup
flows 拿到一个pcap包,用wireshark打开,发现是USB协议,尝试在kali下使用tshark提取,提取失败,发现异常.回到wireshark分析数据.在其中一个数据包中发现了tip 把 ...
- 【转】Java包管理器Maven学习
Maven 引入Jar包的几种情况 1.通过pom.xml中导入的jar包 (1)链接打开http://mvnrepository.com/ (2)搜索罐包,比如我想要的是servlet的api.ja ...
- 【java I/O流总结】基于源码比较FileReader和BufferReader
上一篇博客中,测试分析了FileReader&FileWriter,和BufferWriter&BufferReader之间的性能对比.仅仅只是简单分析.现在我基于源码的角度,来分析B ...
- 动态规划-LCS-Uncrossed Lines
2020-02-11 21:14:18 问题描述: 问题求解: 本质就是LCS. public int maxUncrossedLines(int[] A, int[] B) { int len1 = ...
- 从 ASP.NET Core 3.1 迁移到 5.0
3月中旬,微软官方已经发布了dotnet 5的第一个预览版:5.0.0-preview.1. dotnet core经过前几个版本的发展和沉淀,到3.1已经基本趋于稳定. 所以从.net core 3 ...
- 彻底明白equals和hashCode
equals和hashCode方法 equals 我们知道equals是用来比较两个对象是否相等的,比如我们常用的String.equals方法 @Test public void test() { ...
- 从ISTIO熔断说起-轻舟网关熔断
最近大家经常被熔断洗脑,股市的动荡,让熔断再次出现在大家眼前.微服务中的熔断即服务提供方在一定时间内,因为访问压力太大或依赖异常等原因,而出现异常返回或慢响应,熔断即停止该服务的访问,防止发生雪崩效应 ...
- 【笔记3-24】Python语言基础
环境搭建与语法入门 遇到问题解决问题 积累 英语单词 认真听讲,多敲代码 计算机是什么 计算机的组成 计算机的使用方式 TUI文本交互 GUI图形化交互 windows 的命令行 Shell.Term ...
- GAN的五大有趣应用
引言 你能看出这张照片中面部的共同点吗? 这些人都不是真实存在的!这些面部图像都是由GAN技术生成的. "GAN"这个词是由Ian Goodfellow在2014年提出的,但相关概 ...
- vscode vue 格式化 ESLint 检查 单引号 双引号 函数括号报错问题
vscode vue 格式化 最近重新搞了下电脑,重装了 vscode 软件,在用 vue 写项目的时候,照例开启了 ESLint 语法检查,但是发现在使用 vscode 格式化快捷键的时候(shif ...