字典树&&AC自动机---看完大概应该懂了吧。。。。

目录

字典树

AC自动机

---

字典树

又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。其基本操作有：查找、插入和删除,当然删除操作比较少见。----百度词条

​

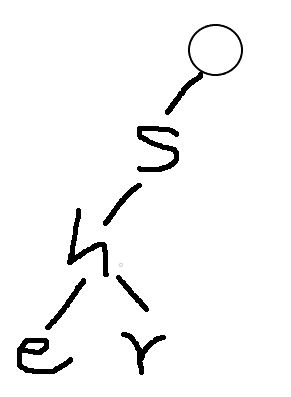
一个插入字符串为she、he、say、shr、her的字典树为

接下来是基本操作：

1.插入

还是上面那幅图

​

首先，根节点是肯定不存在字符的。

然后开始插入吧，首先是she，我们发现根节点的子节点没有存在s，可以插入，s的子节点不存在h，可以插入，h的子节点不存在e，可以插入，然后就是这样

​

我们再插入shr，这时候我们发现根节点的子节点存在s，于是可以和他共享这个节点，记住共享这个词，

继续插入h，发现s的子节点已存在h，于是可以继续共享，最后插入r，我们发现h的子节点没有存在r，于是可以插入

变成这样

​

发现了什么性质了吗？

1.我们插入的时候是从根节点的下一层即子节点开始插入的

2.插入字符串前，先检查这一层中是否存在同一个字符，若存在，则共享，若不存在，则新建一个子节点

 1 void bulid_trie(){
 2
 3     int len=s.length();
 4     int idx=0;//当前字母编号
 5
 6     for(int i=0;i<len;++i){
 7         if(star[idx].son[s[i]-'a']==0){//这个节点不存在
 8             star[idx].son[s[i]-'a']=++flag;//那么就新建一个节点
 9         }
10         idx=star[idx].son[s[i]-'a'];//更新位置以便插入下一个节点
11     }
12
13 }

2.查询

查询操作和插入差不多，就是不用新建子节点而已

例如我们查询she，字母编号分别为1，2，3

从根节点开始，如果根节点的子节点存在s，则更新当前位置为s的编号(1)，继续查找s的子节点是否存在h，存在，更新位置为2，继续查找h的子节点是否存在e，存在，更新位置，然后发现字符串查询完毕，退出循环体，查询结束。

以下代码是查询的时候记录此字符串被查询了几次

 1 int query(){
 2
 3     int len=s.length();
 4     int idx=0;//当前字母编号
 5     for(int i=0;i<len;++i){
 6         //不存在这个字母说明不存在此单词，所以返回0
 7         if(star[idx].son[s[i]-'a']==0)
 8         return 0;
 9         idx=star[idx].son[s[i]-'a'];
10     }
11     star[idx].num++;//此单词被查询了几次
12     return star[idx].num++;
13 }

例如这道题 P2580 于是他错误的点名开始了 https://www.luogu.org/problem/P2580

 1 #include<iostream>
 2 #include<cstring>
 3 #include<math.h>
 4 #include<stdlib.h>
 5 #include<cstring>
 6 #include<cstdio>
 7 #include<utility>
 8 #include<algorithm>
 9 #include<map>
10 using namespace std;
11 typedef long long ll;
12 inline int read(){
13     int X=0,w=0;char ch=0;
14     while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
15     while(isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
16     return w?-X:X;
17 }
18 /*------------------------------------------------------------------------*/
19 const int maxn=1e6;
20 struct node{
21     int num;//该单词结尾遍历完之后的出现次数
22     int son[26];
23 }star[maxn*10];
24 int n,m;
25 string s;
26 int flag;
27 void bulid_trie(){
28
29     int len=s.length();
30     int idx=0;//当前字母编号
31
32     for(int i=0;i<len;++i){
33         if(star[idx].son[s[i]-'a']==0){//这个节点不存在
34             star[idx].son[s[i]-'a']=++flag;//那么就新建一个节点
35         }
36         idx=star[idx].son[s[i]-'a'];//更新位置以便插入下一个节点
37     }
38
39 }
40 int query(){
41
42     int len=s.length();
43     int idx=0;//当前字母编号
44     for(int i=0;i<len;++i){
45         //不存在这个字母说明不存在此单词，所以返回0
46         if(star[idx].son[s[i]-'a']==0)
47         return 0;
48         idx=star[idx].son[s[i]-'a'];
49     }
50     star[idx].num++;//此单词被查询了几次
51     return star[idx].num++;
52 }
53 int main()
54 {
55     ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
56
57     //每个字母都有自己的编号
58     cin>>n;
59     for(int i=1;i<=n;++i){
60         cin>>s;
61         bulid_trie();
62     }
63     cin>>m;
64     for(int i=1;i<=m;++i){
65         cin>>s;
66         int ans=query();
67         if(ans==1)  printf("OK\n");
68         if(ans==0)  printf("WRONG\n");
69         if(ans>1)  printf("REPEAT\n");
70     }
71     return 0;
72 }

复杂度：Trie树其实是一种用空间换时间的算法，它占用的空间很大，但时间是非常高效的，插入和查询的时间复杂度都是O（1）的

AC自动机

当然就是自动AC的一种算法

要学会AC自动机，我们必须知道什么是Trie，也就是字典树。Trie树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

一个常见的例子就是给出n个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。

----来自百度词条

AC自动机算法分为3步：

1.构造一棵Trie树

2.构造失败指针

3.模式匹配

构造字典树上面讲过了

AC自动机的精髓是构造失配指针：

1.根节点所连接的第一层字母fail指针指向根节点！！！（划重点）

2.沿着trie上的字符串去构建，每次取出队列元素时，都要遍历26个字母，如果当前取出元素的子节点存在此字母，设为a，则a的失配指针指向父节点失配指针对应a的节点（是fail指针的子节点）

如下图，s的失配指针指向根节点，h指向其父节点失配指针的对应子节点

​

若不存在该子节点a，则让此点指向父节点失配指针对应a的节点(注意，不是失配指针指向该节点，而是trie树节点指向该节点)

为什么不存在此节点还要让他指向父节点失配指针的对应节点呢？，这是我刚学习的时候一直搞不懂的地方

看个例子，

3个模式串ab,ec，f;文本串abaec，问在文本串中出现几个模式串，output：2

红色是不存在的，为了方便理解（图在下面，旁边的数字表示字母编号）

当我们匹配文本串时，匹配完b节点，发现b节点不存在e，这个时候就可以转移到其父节点b的失配指针（为根节点）所指向的对应子节点e，于是可以继续匹配，如果不这样连接的话，就没法继续往下匹配了

我们假设一下没有连接的情况，即e不指向3，则查询到b时就卡住了，因为节点2并不存在e这个子节点

​

另外，记住AC自动机是多模式匹配算法，这样构建fail指针的目的是为了让匹配时可以一直在trie树上面跳

当前节点匹配失败时可以通过fail指针跳转到其他节点，不用回溯就可以一直匹配下去了

每个节点的失配指针所指向的深度永远是比i小的，因为fail所指向的是永远是后缀

 1 void getFail(){
 2     queue<int>q;
 3     for(int i=0;i<26;++i){
 4         if(tree[0].son[i]){
 5             //括号里面那个是字母编号
 6             tree[tree[0].son[i]].fail=0;//指向根节点
 7             q.push(tree[0].son[i]); //入队
 8         }
 9     }
10     while(!q.empty()){
11
12         int now=q.front();
13         q.pop();
14         for(int i=0;i<26;++i){
15
16             if(tree[now].son[i]){
17
18                 //指向他父亲节点所指向的节点----对应的子节点
19                 //now是父亲节点，fail[now]则是父亲节点失配指针所指向的节点
20                 //这里为什么要这样呢？
21                 //此子节点连接上fail所指向的对应节点，可同时判断以当前匹配的文本串字母
22                 // 为结尾的字符串有多少个 ，fail指向的节点永远是已匹配的字符串的后缀
23                 tree[tree[now].son[i]].fail=tree[tree[now].fail].son[i];
24                 q.push(tree[now].son[i]);
25             }
26             //不存在这个子节点
27             else  //fail[tree[now].son[i]]=tree[fail[now]].son[i];
28
29             tree[now].son[i]=tree[tree[now].fail].son[i];
30             //当前节点的这个子节点指向
31             //父亲节点fail指针的这个子节点
32         }
33
34     }
35
36 }

推荐博客：

字典树： https://blog.csdn.net/forever_dreams/article/details/81009580 

 

AC自动机：

https://bestsort.cn/2019/04/28/402/

https://www.cnblogs.com/cjyyb/p/7196308.html

https://blog.csdn.net/weixin_42146061/article/details/99584227